1 / 1

1. Introduction

    The fuzzy sets theory was introduced by Zadeh (1965) with the objective of providing a mathematical tool for imprecise information treatment. The fuzzy logic based on this theory was initially built from the known concepts of classical logic.

    The fuzzy sets theory (Zadeh, 1965) and the concepts of fuzzy Logic (Zadeh, 1973) are used to translate into mathematical terms the imprecise information expressed by a group of linguistic rules.

    The fuzzy logic permits to create expert systems using linguistic variables to create a rule base. If an expert is able to articulate his action strategy as a group of rules in the form of "If-Then", an algorithm subject to be implemented in a computer can be built, as shown in the seventies (Mandani, 1974 e 1977; Mandani e Assillan, 1975). The result is a rule based expert system in which the fuzzy logic provides the mathematical tools to deal with such linguistic rules.

    The proposed expert system, using the theory of the beach volleyball fundamentals and the concepts of the fuzzy logic, classifies an athlete by a linguistic term (bad, well, very well). The model was implemented using the Unfuzzy Shell (Duarte e Prez, 1999) which support the development of systems with the use of the fuzzy logic.

2. Fuzzy Logic

    The formal concept of fuzzy set was introduced by Zadeh (1965). In the classical theory of the sets, an element from the universe in speech belongs or does not belong to the set, in this case the sets are said "crisp".

    In the theory of the fuzzy sets, there is a membership rank of each element in a set. This concept seems to be very natural and easily realized when examining the sets list below:

• The natural numbers set (c)

• The ASCII set (c)

• The natural numbers beyond 10 set (f)

• The well-off clients set (f)

    There is clearly a fundamental difference between the sets marked with "c" and the sets marked with "f". For example, if a character is shown it can be asserted without any discussion or doubt if this character belongs or does not belong to the ASCII set.

    Thinking based on the classical theory of the sets, the concept of membership of an element to a set gets well defined. The elements of a set A in a determined universe X simply belong or do not belong to the set.

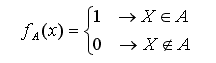
    Zadeh (1965) proposes a broader description, generalizing the characteristic function in the way that it could assume an infinite number of values in the interval [0,1].

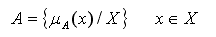
    Where µ(x) is the membership function of x in A and it is defined as a mapping of X in the closed interval [0,1].

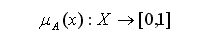
    The membership function indicates how much an element belongs to a set. The support set of a fuzzy set A is the set of elements in the universe x to which $ µ(x)>0.

    A fuzzy set can also be seen as a mapping of a support set in the interval [0,1], what implicates in expressing the fuzzy set by its membership function.

    A fuzzy variable is one in which values are fuzzy set labels. For example, the reception of a determined athlete could be a fuzzy variable assuming the values "errors, broken or good". These values are described by fuzzy sets. Generalizing variable values can be sentences in a specific language. In this context, the reception variable is a linguistic variable.

    The main function of the linguistic variable is to provide a systematic way to an approximate characterization of complex phenomenon or ill defined. In essence, the use of the type of the linguistic description used by human beings, and not the quantified linguistic, permits the treatment of systems that are very complex to be analyzed through conventional mathematical terms.

3. Beach Volleyball

     The analysis of individual and collective performance of the beach volleyball players has demanded the elaboration of objective evaluation criteria of the fundamentals that compound the game structure. Besides the great contribution of existent evaluation systems or programs, to increase this efficiency in this modality, this paper describes the development of a fuzzy system for the performance evaluation of the beach volleyball technical-tactics fundamentals. The need of players development evaluation in games, as well as the training process planning assistance supports the development of a system for performance of beach volleyball technical-tactics fundamentals.

     The individual efficiency analysis of each fundamentals, when executed during a game situation, allows the coach and the players to execute immediate changes as well as to concentrate the attention on those fundamentals in which performance is not reached as intended to. Besides this, it allows to obtain information about the opponent team performance, namely on the fragile points in the execution of the defensive and offensive fundamentals, assuring quick changes in tactics plan established to the game.

     When being used during the competitions of the modality in the team or individual evaluation of all players or teams, the evaluation system also allows the rank of the best couples and the best players in each analyzed fundament.

     This rank facilitated the prizing of the players in competitions of the modality as well as the identification of the relative contribution of each fundamentals to the success of the competition.

     In the training process of this modality, the evaluation system can be used either in the systematic observation of the games as in the analysis success criteria in exercises that involve game situations (Complex Game Exercises I - Attack and Complex Game Exercises II - Transition).

     These uses, when analyzed with the information of the opponent couple performance, enable the previous elaboration of the game tactics plan. The evaluation criteria are the proposed by Coleman (1992 e 1994) to the indoor volleyball and adapted to the beach volleyball. The evaluation criteria were divided in the following way:

• Defensive Fundamentals

1. Reception (error, broken, good)

2. Blockage (error, broken, good)

3. Defense (error, broken, good)

• Offensive Fundamentals

1. Serve (error, easy, good, very good)

2. Raising (error, broken, good)

3. Attack (error, continuing, good)

    Formulas that consider the realized actions weights according to the specific evaluation of each technical-tactics fundamentals were used to calculate the each efficacy.

    There is also a possibility of calculating the percentage efficacy, dividing the efficacy obtained value by 2 (except the serve which is divided by 3) and multiplying by 100. The result percentage of each fundamental that is evaluated in the fuzzy system, informing us if the classification of the athlete was "bad, well or very well". In the Beach Volleyball Evaluation System Fundamentals these calculations are realized through the following way:

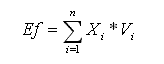
E_f = efficiency of each term
X_i = linguistic term
V_i = Number of occurrence of times of the linguistic term

    The validity of the content, according to Zeller (1990) and Freeman (1990), focus about the extension in which the content of an indicator correspond to the theoretical concept that is being measured. The content validity involves the specification of the concept range and selection of criteria that represent this content. In other words, a measure instrument is valid when it demonstrates that the items that compound it represent appropriately all the important areas of its content .

    The evaluation criteria used in the system were appreciated by experts for content validation. A panel of referees formed by ten physical education professionals and coaches of masculine or feminine couples participants of a Beach Volleyball Contest was the sample. The results of the content analysis of the referees opinions revealed the minimum index of 70% of agreement between the referees, as it was proposed by Serpa (1995), in the evaluation criteria of both offensive and defensive beach volleyball fundamentals.

4. Beach Volleyball Expert System

    The fuzzy modeling presents three evaluation modules; these parts were implemented on Shell Unfuzzy (Duarte e Prez, 1999). The modules were divided according to the evaluation criteria into offensive and defensive.

    Therefore, each of these modules returns a linguistic variable called offensive and defensive, respectively, these results are used in the classification module of the athlete returning the general classification during a match or training. The same membership function was used for three evaluation modules of beach volleyball fundamentals.

    Using the linguistic evaluation weights of the modules with its respective values in the axis of abscises x_o, x_1, x_2, x_n inside a referential set [0, n]. In the ordered axis, it uses the interval [0, 1]. The linear function, generates the membership of the linguistic terms of the evaluation of the defensive, offensive and the classification of the athlete fundamentals, with i = 1,2,3,n, where n is the number of considered linguistic terms. The functions are based on the representation of the membership functions developed by Vioti (1993).

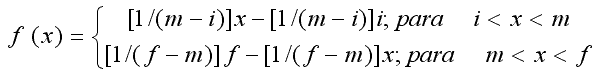
    Where:

• i - initial value of each evaluation weight

• m - maximum value of each evaluation weight

• f - final value of each evaluation weight

    The interference method used was the one proposed by Mandani (1975). In fuzzy expert systems a set of rules type "If-Then" based on fuzzy variables are used (Zadeh, 1992 e Nikolopoulos, 1997).

    Initially the input variables are fuzzified determining of membership value of each linguistic variable. Using these values and the set of fuzzy rules, the inference process is applied obtaining the membership values of the output linguistic variables. Finally, the output variables go through a defuzzification process that consists on converting the fuzzy data to precise numeric values. For this some techniques can be used, such as maximum values, the average of the maximum, center and gravity, local average of the maximum, center of gravity, central point of the area and the center of the average (Eberhart; Simpson; Dobbin, 1996).

    The evaluation of the defensive criterion uses a scale between zero and two; on Table 1 are shown the weights of each defensive linguistic value. In the defensive evaluation module, there are three input variables and an output one. The output variable is determined through the evaluation of 27 rules in the interference machine; the interference machine uses the minimum and the maximum operators.

Table 1 - Reception, Defense and Blockage

    In this example, using as starting the following: reception values = 1.2, blockage = 1.5 and defense = 2.0, the rules activated by the interference machine will be:

• IF Reception is Broken AND Blockage is Continued AND Defense is Good THEN Defensive is Good.

• IF Reception is Broken AND Blockage is Good AND Defense is Good THEN Defensive is Good.

    The membership value to the defensive module obtained by the inputs seen above is 1.0.

    The evaluation of the offensive criterion uses a scale of weights between [0 and 3] except the serve criterion that uses a scale between [0 and 4], as shown on Table 2 and Table 3 below:

Table 2 - Serve

Table 3 - Attack and Raising

    In the offensive evaluation module, there are also three input variables and an output one. The output variable is determined through the evaluation of 36 rules in the inference machine. The minimum and the maximum operators are used.

    In this example, using as starting the following: serve values = 1.3, raising= 1.0 and attack= 0.8, the rules activated by the inference machine will be:

• If Serve is Easy and raising is Error and Attack is error, then Offensive is Bad.

• If Serve is Easy and Raising is Error and Attack is Continued, then Offensive is Bad.

• If Serve is Easy and Raising is Broken and Attack is Error, then Offensive is Good.

• If Serve is Easy and Raising is Broken and Attack is Continued, then Offensive is Well.

    The membership value for the offensive module obtained with the input values mentioned above is 0.934.

     In the classification module of the athlete the results obtained from the offensive and defensive modules are used, the linguistic values for this module is on Table 4 below:

Table 4 - Defensive and Offensive

    Two starting variables are used in this module, whose values are the outputs of the other two modules. As in this module, there are just two variables and as they have just three linguistic terms, this module has just nine rules.

    Using as example the previous modules results (defensive variable= 1.0 and offensive variable= 0,934) the following rule will be activated:

• If Defensive is Well and Offensive is Well, then Classification is Well

    The membership value for the classification module of the athlete obtained with inputs of 1,000 for the defensive and of 0,934 for the offensive is 1,000 for the classification of the athlete.

5. Conclusion

    Due to the used criteria, it is possible to work with the three modules together in order to determine the biggest difficulties and the best classifications for each evaluated athlete by the fuzzy system.

    At this moment the system is compounded by Beach Volleyball Evaluation Systems Fundamentals, and with this system, we can get to recover the value of the starting for the defensive end the offensive criteria of each athlete, in order to not to have only on evaluation C crisp of each athlete, but one fuzzy evaluation that provides more details of the development of the athletes.

    As a further essay we intend to put our own Beach Volleyball Evaluation Systems Fundamentals, a module that makes the fuzzification and deffuzification of the criteria, in order to not to be necessary to use a Shell of others.

References

• Coleman, J. (1992). Evalution of blocking. Coaching Volleyball, 15: 6 -10.

• Coleman, J. (1994). Some new thoughts about the evalution of blocking. Coaching Volleyball, 21: 10 - 13.

• Duarte, O. and Prez, G. (1999). Unfuzzy: fuzzy logic system analysis, design simulation and implementation software. In: Proceedings of the Eusflat-Estylf Joint Conference.

• Eberhart, R., Simpson, P., and Dobbins, R. (1996). Computational intelligence pc tools. New York: AP Professional.

• Freeman, F. S. (1990). Teoria e prática dos testes psicológicos. Lisboa: Fundação Calouste Gulbenkian.

• Mandani, E. H. (1977). Applications of fuzzy logic to approximate reasoning using linguistic synthesis. In : Proceedings of the IEEE (Trans. Computers), 126: 1182- 1191.

• Mandani, E. H. and Assillan, S. (1975). An experiment in linguistic synthesis with a fuzzy logic controller. International Journal of Man-Machine Studies, 7:1- 13.

• Mandani, E. H. (1974). Application of fuzzy algorithms for control of simple dynamic plant. In: Proceedings of the IEEE (Control and Science), 121: 298-316.

• Nikolopoulos, C. (1997). Expert Systems: Introduction to first and second generation and hybrid knowlegdebased systems. London: Marcel Dekker Press.

• Serpa, S. O. (1995). A relação interpessoal na díade treinador-atleta; desenvolvimento e aplicação de um inventário de comportamentos ansiogênicos do treinador. PhD thesis, Universidade Técnica de Lisboa.

• Vioti, G. (1993). Fuzzy logic in c. Dobb's Journal, 5: 154-160.

• Zadeh, L. A. (1965). Fuzzy sets. In: Proceedings of the IEEE (Information and Control), 8:338-353.

• Zadeh, L. A. (1973). Outline of a new approach to the analysis of complex system and decision processes. In: Proceedings of the IEEE (Transactions on Systems Man and Cybernetics), 3: 28-44.

• Zadeh, L. A. (1992). The calculus of fuzzy if-then rules. AI Expert, 7 : 23 - 27.

• Zeller, R. A. (1990). Validity. In : Educational Research, Methodology and Measurement an International Handbook. New York: Pergamon Press, 322-330.

	http://www.efdeportes.com/ · FreeFind
revista digital · Año 10 · N° 83 | Buenos Aires, Abril 2005   © 1997-2005 Derechos reservados