efdeportes.com

Proyecto de matemática superior para las especialidades biomédicas 

de la Universidad de Ciencias Médicas de Pinar del Río, Cuba

Project higher mathematic for biomedical specialties Medical University of Pinar del Rio, Cuba

 

*Universidad Nacional de Educación UNAE (Ecuador)

**Departamento de Informática

de la Universidad de Ciencias Médicas

(Cuba)

PhD. Ignacio Estévez Valdés*

iestevez@princesa.pri.sld.cu

Lic. Ania Sosa Fernández**

anias@fcm.pri.sld.cu

 

 

 

 

Resumen

          El vertiginoso desarrollo de la Ciencia y la Técnica ha interrelacionado distintas especialidades del saber y por lo tanto la necesidad de un "lenguaje común" para el entendimiento entre ellos. Sin proponérselo, la matemática conjuntamente con la estadística y las probabilidades, han ido ocupando este lugar dentro de las ciencias biomédicas. La necesidad de incorporar al diario quehacer de los especialistas, en particular aquellos de las Ciencias Básicas Médicas, el manejo de un lenguaje como una herramienta indispensable para la conceptualización teórica y cuantitativa de los problemas biomédicos, ha hecho necesario desarrollar un curso de matemática en la especialidad de ciencias básicas, el cual no está exento de dificultades reportadas en su retrospectiva. Problemas tales como: densidad del contenido en el tiempo asignado, insuficiente nivel de partida, y problemas con la base material de estudio entre otros, hacen pensar en la conveniencia de buscar alternativas que hagan más viable el cumplimiento de los objetivos propuestos en el programa.

          Palabras clave: Especialidades biomédicas. Ciencias biomédicas. Matemática en medicina.

 

Abstract

          The rapid development of science and technology has brought, among other consequences, the inter-relation between specialists from different domains of knowledge, and therefore the need for a "common language" for their understanding. Unintentionally, the mathematics together with the field of statistics and probability, have increasingly came to occupy this place in the biomedical sciences. The need to incorporate to the daily work of specialists, in particular those in the Basic Medical Sciences, the management of a language as an indispensable tool for theoretical and quantitative conceptualization of biomedical problems has made it necessary the development of a mathematics course for specialization in basic science, which is not without difficulties when reported in retrospective. Problems such as dense content in the allocated time, insufficient prior knowledge, and problems with study materials, among others, suggest the desirability of looking for alternatives that make it more feasible the achievement of the objectives proposed for the program.

          Keywords: Biomedical specializations. Biomedical sciences. Mathematics in medicine.

 

Recepción: 10/08/2015 - Aceptación: 17/11/2015

 

 
EFDeportes.com, Revista Digital. Buenos Aires, Año 20, Nº 211, Diciembre de 2015. http://www.efdeportes.com/

1 / 1

Introducción

    La educación de Postgrado tiene como objetivo central la formación académica de Postgrado y la superación continua de los egresados universitarios durante su vida profesional. Dentro de la formación posgraduada está las especialidades biomédicas que tiene una importancia vital en la calidad de los graduados en medicina de cualquier universidad cubana, pues ellos conformarán el claustro que al menos en los dos primeros años de la carrera forman a los futuros profesionales de la salud.

    En las referidas especialidades, se imparte en primer año la asignatura de matemática que consta de 96 horas presenciales y 8 temas de estudio, en el programa relativo a esta asignatura en lo que respecta a evaluación aparece escrito según Antón (1999) la atención que debe darse a las evaluaciones parciales debe ser extrema, pues las dificultades de base de los estudiantes, producto del excesivo tiempo que llevan desvinculados de la matemática, son grandes.

    Se reconoce de forma explícita en el programa, que no está asegurado el nivel de partida de los estudiantes, eso sumado, a que es común escuchar con frecuencia a estudiantes de medicina exponer la idea que relaciona el estudio de la medicina con el uso nulo de la matemática, esto por supuesto, siempre es manejado por algunos alumnos que por diversas razones sienten aversión hacia la matemática u otras ciencias estrechamente relacionadas a esta. El profesor de matemática está por naturaleza, envuelto en problemas y preguntas, pero hay una latente que siempre se hace por parte de los educandos, al menos a partir del nivel medio: ¿Para qué me servirá este contenido matemático en mi carrera o en mi vida?

    Las matemáticas, y en especial la matemática estadística poseen una alta aplicabilidad en las ciencias humanas y sociales (García y Ferrer, 1966), desde la estadística para la administración y la economía (Haeussler y Paul, 2003; Levin, Balderas, del Valle y Gómez, 2004), las ciencias de la Actividad Física y el Deporte (Calero y Suárez, 2005; Calero, 2007, 2009, 2010, 2012), los procesos de investigación educativos como métodos eficaces para demostrar hipótesis de trabajo (Kish, 1996; Sánchez, 2014) hasta la aplicabilidad en las ciencias médicas para establecer, entre otros aspectos, patrones de movilidad e infectividad de las enfermedades (Juez y Díez, 1996; Martínez, 2003; Martín y Luna, 2004).

    El utilitarismo de la ciencia y su dañino impacto es algo reconocido a nivel internacional, es cierto que no es siempre fácil contestar a esta pregunta, no por falta de argumentos convincentes, el problema estriba en que los cuestionadores por lo general no están aptos para entender, al menos, en el momento de cuestionar.

    Con estas agravantes, en cuanto el profesor se enfrenta al programa queda con muchas dudas de cómo hacer para que se cumplan los objetivos dispuestos en el mismo, el contenido a tratar en el tiempo dispuesto es sumamente ambicioso, cuando analizamos los programas más o menos parecidos establecidos en universidades politécnicas a estudiantes que si viene de una enseñanza precedente cercana y con motivación o inclinación por carreras de alto contenido matemático, es imposible dejar de sorprenderse.

I.     Programa Universidad de Ciencias de la Informática (Curso 2003-2004).

  • Asignatura: Matemática I

  • Temas 1: Limite de funciones de una variable real

  • Tema 2: Calculo diferencial de funciones de una variable real.

  • Tema 3: Calculo integral de funciones de una variable real.

  • Tema 4: Ecuaciones diferenciales ordinarias.

  • Total Horas: 72

  • Solo 4 temas. Diferencia en horas con El programa de Biomédicas: 24

II.     Programa Universidad de Pinar del Río “Hermanos Saíz Montes de Oca".

  • Carrera: Ingeniería en Telecomunicaciones y Electrónica.

  • Asignatura: Matemática Superior I.

  • Tema 1: Límite y continuidad de funciones reales de una variable real.

  • Tema 2: Cálculo diferencial de funciones reales de una variable real.

  • Tema 3: Cálculo integral de funciones reales de una variable real.

  • Total de Horas: 96

  • Solo 3 temas con la misma cantidad de horas.

III.     Programa Universidad de Pinar del Río “Hermanos Saíz Montes de Oca".

  • Carrera: Ingeniería Informática.

  • Asignatura: Matemática I.

  • Tema 1: Funciones y límites.

  • Tema 2: Cálculo diferencial de funciones reales de una variable y varias variables real.

  • Total de Horas: 96

  • Solo 2 temas con la misma cantidad de horas.

IV.     Programa Universidad de Pinar del Río “Hermanos Saíz Montes de Oca".

  • Carrera: Agronomía.

  • Asignatura: Matemática I

  • Tema 1: Nociones de álgebra matrices y vectores.

  • Tema 2: Cálculo diferencial de funciones reales de una variable.

  • Tema3: Cálculo integral y aplicaciones para funciones de una variable.

  • Total de horas: 70

  • 28 horas menos que el programa en cuestión, pero solo 3 temas.

V.     Programa Universidad de Pinar del Río “Hermanos Saíz Montes de Oca".

  • Carrera: Geología

  • Asignatura: Matemática I

  • Tema 1: Funciones y límites.

  • Tema 2: Cálculo diferencial de funciones reales de una variable y varias variables real.

  • Tema 3: Cálculo integral de funciones de una variable real.

    En cuanto al programa que analizamos en este trabajo destacaremos explícitamente los 8 temas referidos anteriormente:

    Los tipos clases indicados son: Conferencia, Clase Práctica y Seminarios.

    Otras asignaturas que se imparten en el semestre:

Estado del arte

    En base a las problemáticas planteadas con anterioridad, consideramos que si se determinan las principales invariantes del curso para así priorizar su tratamiento, se emplean un grupo de problemas de aplicación biomédica, se implementa el laboratorio como forma docente y se usa un software simbólico, entonces se puede lograr un curso donde al menos el cumplimiento de los objetivos este a tono con las aspiraciones reales y futuras de los especialistas en formación.

    La tecnología educativa ha servido de apoyo para aumentar la efectividad del trabajo del profesor, sin llegar a sustituir su función educativa y humana, así como organizar la carga de trabajo de los estudiantes y el tiempo necesario para su formación integral, para elevar la motivación hacia la enseñanza y el aprendizaje, y garantizar la asimilación de lo esencial.

    Podemos empezar aceptando que la forma clásica de enseñanza no es suficiente para hacer frente a la situación actual, y debe estar apoyada por nuevos y diferentes métodos de enseñanza frente a los nuevos cambios y expectativas. Lo siguiente puede subsanar las actuales deficiencias:

    Meza (2013) plantea “Tenemos que la enseñanza de la matemática asistida por computadora tiene orígenes ubicables más allá de los cincuenta años de antigüedad. Paulatinamente, y muy relacionado con los desarrollos tecnológicos, se han dado cambios que parecen favorecer el uso de computadoras y de software en la enseñanza de la matemática, permitiendo no solo una mayor cobertura de temas sino la implantación de estrategias didácticas y de abordajes pedagógicos innovadores”.

    Según Castañeda (2001): “La introducción del asistente matemático como herramienta de trabajo en la Disciplina Matemática actuará como un nuevo elemento Didáctico Integrador en las carreras de Ciencias Técnicas. El uso del asistente matemático se ha ido incrementando paulatinamente y actualmente se hace una necesidad como un elemento más dentro del proceso Enseñanza–Aprendizaje”.

    Miyar (2007) refiere: “Un Asistente Matemático es una herramienta computacional que permite dar solución a problemas de manera más asequible para el estudiante y favorece la interiorización de los conceptos y procedimientos de modo que estos permanezcan a más largo plazo, su carácter interactivo permite una retroalimentación inmediata, además de ampliar el abanico de manipulaciones posibles y el de visualización. Su capacidad gráfica facilita la integración de diversas imágenes conceptuales, que constituyen un obstáculo para el aprendizaje”.

    También Ortega (2002) expone que estos sistemas pueden favorecer el protagonismo del alumno, ya que el uso de un Sistemas Algebraicos Computarizados (SCA) reduce los cálculos y permite que el alumno oriente su esfuerzo hacia la exploración y experimentación de los hechos y principios que se van introduciendo.

    Cook (1999) expuso que el manejo de un SCA ofrece una nueva dialéctica de colaboración entre los alumnos y entre alumnos y profesor, favoreciendo la aparición de contextos que conducen hacia el denominado aprendizaje colaborativo.

    En el caso que nos ocupa hemos decidido usar el paquete Derive en el curso de matemática por tener poco peso, y presentar una sintaxis casi igual a la usual en los textos matemáticos. Derive es un programa de matemática para computadoras, procesa variables, expresiones, ecuaciones, funciones, vectores y matrices. Al igual que una calculadora científica sirve para trabajar con números. Derive puede realizar cálculos numéricos con algebra, trigonometría, análisis. La versión que se empleó y empleará a lo largo de este trabajo es la 5.02, en el mercado desde junio 2000, Espacio para cálculos: 895.7 MB. Memoria libre: 99.9 %. El aspecto más sobresaliente de DERIVE es su trabajo simbólico unido a sus capacidades gráficas.

    Según Macías (2007) las imágenes, dibujos, diagramas, gráficos, bosquejos y esquemas, son aspectos particulares dentro del proceso de visualización, ya que con éstos se puede representar un fenómeno de cualquier índole o formar en la mente una imagen visual de algo abstracto. Aunque a primera vista un manipulador simbólico puede interpretarse como una calculadora muy potente, en realidad se trata de un laboratorio matemático completo con posibilidades de edición y presentación visual que permiten darle la apariencia de un escrito matemático clásico.

    Para Fernández (2000) la utilización de la tecnología de computación puede ser un medio de enseñanza al igual que un libro o video, pero con un mayor nivel de interactualidad. Gamboa (2007) plantea, no obstante es importante tener en cuenta: Investigar y documentar el proceso de interacción del estudiante con las herramientas tecnológicas cuando resuelve problemas, observando aspectos relacionados con su uso, las representaciones que emplea, el tipo de conjeturas y conclusiones que obtiene, proporciona argumentos para identificar qué tipo de actividades son las que se tienen que plantear para alcanzar una mayor comprensión de los conceptos matemáticos, así como identificar las ventajas y desventajas que se presentan al trabajar con estas herramientas.

    Es el Derive, una herramienta excelente para hacer y aplicar matemáticas, para documentar el trabajo de matemáticas y para aprender y enseñar matemáticas.

    Existen muchos software con fines matemáticos entre otros a parte del Derive, están le Matlab, Mathematica, Eureka, Reduce, Calcula, Mathcad, etc., en nuestro país desde la década de los 90 hasta nuestros días hay presencia de estos en la docencia relativa a la matemática, ejemplo de estos son los trabajos:

    No obstante todo lo antes expuesto, es siempre justo en lo relativo al uso de las tecnologías en las clases y más aun en las clases de matemática, recordar siempre lo referido por el profesor Pérez (2001): “La cuestión de la utilidad de Sistemas Algebraicos Computarizados (CAS) no parece ser la disyuntiva de todo o nada, sino de un uso juicioso de la herramienta. Naturalmente, lo que pueda significar ‘juicioso’, está abierto al debate”. También es de interés para los profesores señalar que según Gamboa (2007) la implementación de la tecnología en el salón de clases exige al profesor planificar, cuidadosamente, las actividades con las que se va a trabajar y estar preparado para resultados inesperados. En lo que se puede considerar la hipótesis de este proyecto, se destaca el laboratorio práctico de matemática como forma docente a emplear en el curso sustentado entre otras las ideas de Gamboa (2007) que plantea:

    La introducción de la tecnología en el salón de clases ha cambiado la forma en que se lleva a cabo el proceso de enseñanza y aprendizaje de las matemáticas. A diferencia del enfoque algorítmico que se le ha dado a la enseñanza de esta disciplina, ésta se puede desarrollar ahora en un ambiente de descubrimiento y reflexión. También en la comentada hipótesis se destaca los problemas de aplicación en el curso, no solo como elemento del necesario conocimiento si no también como acción de motivación. El abordaje rutinario en la enseñanza ha generado una separación entre los conceptos teóricos y su aplicabilidad, lo que ha provocado en los alumnos desinterés por las matemáticas. (p. 11-44)

    Haciendo consideraciones sobre las potencialidades reales de contar con un banco de problemas matemáticos de aplicación biomédica, relativos a los temas tratados en el programa de matemática para las especialidades biomédicas, es importante señalar la disponibilidad de una bibliografía basta y variada que en su contenido práctico consta de múltiples problemas con una adecuada actualidad e interés, dentro de esta bibliografía entre otros, se dispone de los siguientes títulos:

Metodología

Objetivo general

    Diseñar un conjunto de acciones en el proceso de enseñanza y aprendizaje de la asignatura Matemática para especialidades biomédicas, que responda a los intereses, posibilidades y necesidades del egresado, en su formación.

Objetivos específicos

  • Determinar las invariantes de los contenidos descritos en el programa, que incidan con fuerza en la posibilidad de resolver problemas biomédicos, que conduzcan al uso de modelos matemáticos.

  • Emplear el paquete estadístico Derive 5 versión 5.04 en la conformación de clases prácticas de laboratorios de matemática.

  • Incentivar el trabajo cooperativo entre estudiantes en la solución de problemas integradores en la clase de laboratorio.

  • Garantizar el nivel de partida adecuado para las asignaturas de las especialidades biomédicas precedentes al curso de matemática.

  • Confeccionar un material didáctico impreso y digital, relativo a ejercicios de aplicaciones biomédicas por cada unidad temática a tratar en el curso.

Aspectos generales del estudio

    La investigación se desarrollará en el periodo correspondiente entre los cursos 2011-2012 y 2016-2017, en la Universidad de Ciencias Médicas de Pinar del Río. Es una investigación de evaluación, longitudinal prospectiva con elementos retrospectivos.

Definición del universo de estudio y muestra

    El universo de estudio estará constituido por todos los residentes de Especialidades Biomédicas de la Universidad de Ciencias Médicas de Pinar del Río.

Método

    Se emplearan técnicas de análisis tales como: Observación, entrevista, revisión documental, cuestionarios y opinión de expertos.

    La variable dependiente es la calidad del proceso docente educativo en el desarrollo de la asignatura de interés en esta investigación (Y(Xi)), y las independientes (Xi), con i=1,2,…,9; estarán determinadas por:

  • Motivación de los estudiantes por la asignatura antes, del curso (X1).

  • Motivación de los estudiantes por la asignatura después, del curso (X2).

  • Resultados de las evaluaciones parciales en el tiempo (X3).

  • Resultado de la evaluación final(X4).

  • Repercusión de la formación matemática en la docencia a desarrollar por los residentes(X5).

  • Criterios de los profesores de las asignaturas subsecuente: Física I, II y III, Química General, Química Orgánica; Química-Física I y II; Métodos de la Investigación, relacionados con el aseguramiento del nivel de partida demostrado por los alumnos de los distintos cursos (X6).

  • Posibilidad que demuestren los egresados de la asignatura, al pasar un año de haberla cursado, para identificar un modelo matemático estudiado en el curso, que dé respuesta a una situación problémica relativa a su especialidad(X7) .

  • Grado de satisfacción mostrado por los residentes, después de pasar un año de haber cursado la asignatura matemática (X8).

  • Edad del residente (X9).

Tabla 1. Operacionalizacion de las variables

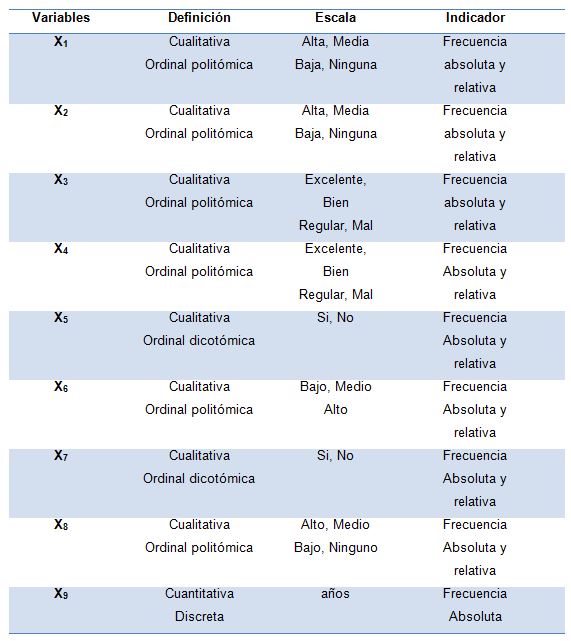
    La información obtenida mediante los diferentes instrumentos aplicados se procesará mediante el empleo de elementos de estadística descriptiva tales como tablas y gráficos.

Conclusiones

    Con este proyecto se debe alcanzar los resultados siguientes:

Bibliografía

Otros artículos sobre Educación Física

www.efdeportes.com/

EFDeportes.com, Revista Digital · Año 20 · N° 211 | Buenos Aires, Diciembre de 2015
Lecturas: Educación Física y Deportes - ISSN 1514-3465 - © 1997-2015 Derechos reservados