La Rosa Trigonométrica, un medio dinámico para la enseñanza  y el aprendizaje de conocimientos trigonométricos elementales The Trigonometric Rose, a dynamic mean by the learning and teaching of elemental trigonometric knowledges
	Centro Universitario Municipal (CUM) Caimanera, Guantánamo (Cuba)	Lic. Angel Deslis Mendoza Dr. C. Beatriz María San Juan Azze adeslis@caimanera.cug.co.cu
	Resumen           Este artículo presenta un medio de enseñanza dinámico creado por el autor. Dicho medio posee características distintivas en relación a otros existentes que viabilizan el proceso de enseñanza-aprendizaje de los conocimientos trigonométricos básicos. Esta contribución práctica se emplea en el análisis de las propiedades de las funciones trigonométricas en la educación preuniversitaria. Presupone la creación del medio la siguiente valoración: se revelan insuficiencias en el aprendizaje de tales conocimientos por parte de los alumnos, condicionado por contradicciones esenciales entre el contenido y la forma en que el maestro enseña, donde se implica la creación de medios apropiados. Tal es el caso de la Rosa Trigonométrica, que juega un papel esencial durante la puesta en práctica de un método de representación dinámica de la relación gráfico - propiedades de las funciones trigonométricas.           Palabras clave: Matemática. Medios de enseñanza dinámicos. Rosa trigonométrica.   Abstract           This paper presents a teaching dynamic means created by author. This medium has distinctive features in relation to other existing viable the teaching-learning process of basic trigonometric knowledge. This contribution is used in the practice analysis of the properties of the trigonometric functions in preuniversity education. Means creation presupposes the following assessment: reveal inadequacies in learning such knowledge by students, conditioned by essential contradictions between the content and the way in which the teacher teaches, which involves creating appropriate means. Such is the case of Rose Trigonometrical, which plays an essential role during the implementation of a method of representing graphical relationship dynamics - properties of trigonometric functions.           Keywords: Mathematic. Dynamic teaching means. Trigonometric Rose.
	EFDeportes.com, Revista Digital. Buenos Aires, Año 18, Nº 190, Marzo de 2014. http://www.efdeportes.com/

1 / 1

Introducción

    En la Didáctica como ciencia en general y en la Didáctica de la Matemática en particular, las funciones y sus propiedades constituyen un contenido que se estudia en diferentes niveles y subsistemas de la educación cubana y foránea. Estos contenidos forman parte de un sistema de relaciones, en el cual se revelan estrechos vínculos cognitivos y como objetos entre ecuaciones, gráficos y propiedades.

    En especial, en este documento científico se trata la relación gráfico-propiedades de las funciones trigonométricas. La apropiación de este contenido trasciende en el desarrollo de una habilidad generalizada: relacionar gráfico y propiedades de funciones, dada para el estudio de todo tipo de función en Matemática. Por el amplio nivel de aplicaciones que tienen las funciones trigonométricas en diversas esferas de la realidad, el estudio y tratamiento de estas, merece una atención especial por parte de la comunidad de matemáticos.

    Con el avance de la Revolución Científico-Técnica y el auge de las ciencias, los medios de enseñanza experimentan cambios y se perfeccionan a la luz del propio desarrollo de la Matemática y sus aplicaciones. Este hecho impone que el maestro emplee no solo medios tan simples como una lámina o un objeto natural en el momento exacto que el proceso de enseñanza lo requiera, sino que se necesita crear otros medios en los que el aprendiz sea un agente activo en la construcción de los conocimientos. Tampoco el único recurso activo que es posible emplear para aprender matemática u otra ciencia está relacionado con el uso de los sistemas de aplicación, no siempre dominado por parte de los usuarios.

    Las razones expuestas motivan al autor a la elaboración de una tesis doctoral de cuyo eje de construcción teórico – práctica emerge un método de representación dinámica que tiene como sustento material los medios dinámicos como la Rosa trigonométrica. Esta dinamiza el proceso de enseñanza – aprendizaje de las funciones trigonométricas al lograr una mejor visualización del comportamiento de las propiedades y permitir la manipulación secuencial y predeterminada por parte de maestros y alumnos.

    La construcción de la Rosa Trigonométrica no requiere del empleo de recursos costosos, por lo que se convierte en un medio de enseñanza rentable y adecuado para aprender trigonometría.

Materiales y métodos

    Para el proceso constructivo del medio: cartulina, pegamento, papeles de colores, instrumentos tradicionales de dibujo. De esta manera se obtiene la Rosa trigonométrica en lámina para el uso del maestro en una clase presencial. Otra variante la constituye la Rosa en madera, en este caso se sustituye el papel de colores por pintura. Se necesitan además accesorios, que se diseñan en acrílico o materiales similares (radio móvil y péndulo articulado a este que funciona por gravedad)

    La variante portátil de la Rosa es la digitalizada, obtenida a partir de un simulador en flash.

    Para la concepción del método dinámico: se emplean entrevistas, observaciones participantes y registros de experiencias donde se presenta la relatoría del uso del medio en el aprendizaje de la trigonometría. A partir de la inducción-deducción y la modelación básicamente se obtiene el método de representación dinámica.

Resultados del trabajo

    Como resultado del trabajo se obtiene un medio de enseñanza dinámico creado por el autor sustentado en un método de representación dinámica. Se presentan sus características distintivas, y se proponen ejemplos concretos de su uso en variadas temáticas de contenidos trigonométricos. Dado lo novedoso del medio y su pertinencia para la implementación del método dinámico propuesto, resulta de interés que se conozca en detalle todo cuanto concierne a dicho medio de enseñanza.

Características distintivas de la Rosa Trigonométrica

    Es un medio plano que contiene grabado cuatro circunferencias concéntricas, con centro común en el origen de un sistema de coordenadas rectangulares. Estas circunferencias determinan tres anillos circulares, de manera que si se considera la dirección desde dentro hacia fuera, se consigan los ángulos positivos expresados en grados sexagesimales, en radianes expresados por los coeficientes de p (pi) en el anillo intermedio y los ángulos negativos en grados sexagesimales en el anillo exterior (Figura 1).

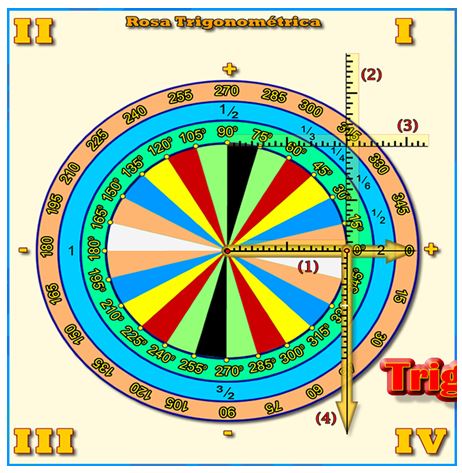
Figura 1. La Rosa trigonométrica, medio creado por el autor

para la enseñanza de los conocimientos trigonométricos elementales

    El círculo interior limitado por la primera circunferencia, se divide en cuatro cuadrantes que a la vez se subdividen en seis sectores circulares con amplitudes iguales a 15˚. Los sectores se colorean de manera que en el primer cuadrante los ángulos notables terminen en un color primario (amarillo, rojo, azul); los axiales con colores neutros (blanco, negro) y el resto con colores secundarios (verde, anaranjado). La combinación de colores que se obtiene en el resto de los cuadrantes es el resultado de las simetrías tanto axiales como central respecto a los ejes coordenados y al origen respectivamente.

    Contiene además tres escalas fijas: escala (1) situada sobre el semieje OX con longitud igual a la longitud del radio seleccionado (preferentemente un múltiplo de 10). Las unidades de medida representan la décima parte de la longitud del radio. Esto posibilita obtener valores aproximados hasta el orden de las centésimas y sirve para determinar el coseno de los ángulos.

    La escala (2) está situada en la perpendicular al eje X en el punto T (1; 0) del sistema de coordenadas y tiene iguales características a la escala (1) pero con longitud mayor. Dicha escala sirve para determinar la tangente de ciertos ángulos.

    La escala (3) es similar a la escala (2) y está ubicada sobre la perpendicular al eje Y, en el punto S (0; 1) del sistema de coordenadas. Esta permite determinar la cotangente de los ángulos.

    Como accesorios contiene un radio móvil que consiste en un listón plástico transparente. Este listón tiene grabado, por debajo, una línea que sirve como indicador de medidas para las escalas de la tangente y la cotangente en el punto de intersección con éstas.

    Otro accesorio lo constituye otro listón plástico transparente insertado al radio móvil en su extremo; que funciona por gravedad. El mismo posee una cuarta escala similar a las demás y permite determinar el seno del ángulo seleccionado. Posee además una línea similar al radio móvil que indica la medida del coseno del ángulo cuando intercepta a la escala (1). A continuación un resumen de las escalas tratadas y que en lo adelante sólo se hace referencia al número asociado. (Figura 1)

• Escala (1): Para la lectura del coseno del ángulo.

• Escala (2): Para la lectura de la tangente del ángulo.

• Escala (3): Para la lectura de la cotangente del ángulo.

• Escala (4): Para la lectura del seno del ángulo.

    Estas escalas no se conciben al azar sino que se fundamentan en conceptos básicos establecidos para cada razón trigonométrica, desde el surgimiento de la Trigonometría. Tales conceptos aún siguen vigentes en nuestros programas. En tal sentido se define en el texto básico Matemática 10º grado:

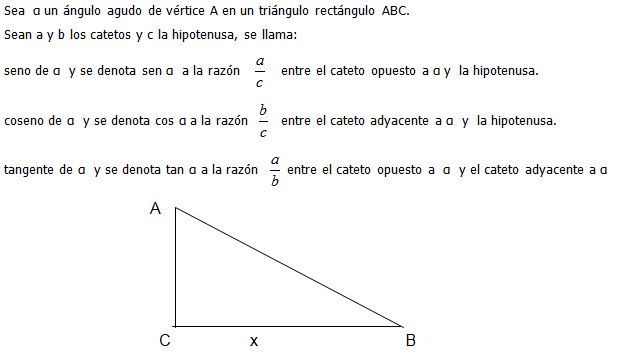
    Estas razones trigonométricas tienen sus limitaciones cuando se enmarcan a los ángulos agudos de un triángulo rectángulo. Para el resto de los ángulos incluyendo a los llamados axiales es necesario ubicarlos en un sistema de coordenadas rectangulares y con mayor precisión, en una circunferencia trigonométrica que es la idea inicial como base para la concepción de la Rosa trigonométrica.

    Ahora se puede justificar que:

    Al dejar constancia de las características distintivas de la Rosa, nos proponemos relacionar las principales funciones derivadas de sus posibilidades de empleo para la unidad escogida; desde sus inicios hasta la subunidad que se corresponde con el tema de investigación.

Funciones específicas

• Cálculo de razones trigonométricas de cualquier ángulo sin el uso de tablas trigonométricas ni las fórmulas de reducción con valores admisibles hasta el orden de las centésimas.

• Demostración de la identidad fundamental sen ² α + cos ² α = 1

• Resolución de ecuaciones trigonométricas sencillas.

• Reducción de amplitudes de ángulos de grados sexagesimales a radianes y viceversa, para ángulos múltiplos enteros de 15˚.

• Determinación de ángulos positivos, negativos y coterminales.

• Análisis de las funciones trigonométricas y sus propiedades sin apoyo de la representación gráfica.

Situaciones de aprendizaje concretas

    A continuación se ofrecen algunas situaciones de aprendizaje según las temáticas donde la Rosa trigonométrica tiene posibilidades de empleo. Esto permite adiestrar tanto a docentes como a estudiantes en el uso de este novedoso medio y ponerlos en mejores condiciones al abordar posteriormente lo esencial de los temas.

    Se establece un símil, entre lo que se establece para las clases actuales y lo que se desea introducir con el uso del medio. Por otra parte, los contenidos relacionados con la enseñanza-aprendizaje de la trigonometría están incluidos desde el 9no grado hasta el 12mo grado de la educación general y en los primeros años de la formación inicial del docente.

Ejemplo 1. Determinación de razones trigonométricas para ángulos pertenecientes al I Cuadrante

    Procedimiento normal establecido

    Sea α = 45˚ el ángulo escogido, en este caso se procede normalmente de la forma siguiente:

    Para determinar el seno y el coseno se busca en la tabla de valores trigonométricos y según sea el caso a través de la intersección entre filas y columnas se obtiene:

    Para determinar la tangente se busca en la tabla y se concluye que:

    tan 45˚ = 1 (valor exacto para este ángulo).

    Otra vía que tiene disponible el estudiante para el caso de los ángulos notables, es memorizarlos según la tabla siguiente:

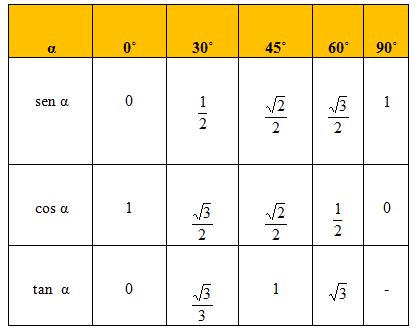
Empleando la Rosa (véase figura 1)

    En este caso para mayor efectividad en los cálculos el medio debe permanecer en posición de plano vertical. Las piezas adicionales (radio móvil y péndulo) pueden emplearse simultáneamente o por separado, según la función deseada. Además se pone de manifiesto el principio de la composición de movimientos de rotación- traslación en el plano.

    Para determinar las razones trigonométricas de α = 45˚, procedemos así:

• Fijamos el radio móvil por su extremo en el valor que indica 45˚, en el anillo más interior.

• Como la escala (4) al fijarse al radio móvil en su extremo, cae en forma de péndulo , entonces es perpendicular al semieje OX ; por lo que para ángulos agudos siempre quedará determinado un triángulo rectángulo lo cual asegura la validez de las escalas (1) y (4) de manera tal que:

    Los valores aproximados obtenidos son admisibles tanto desde el punto de vista práctico como teórico donde siempre existe un límite de error que en este caso es de 1 . 10^-2 .

Ejemplo 2. Demostración de la identidad sen ² α + cos ² α = 1

    La demostración que se orienta aparece en el teorema 1a) del texto básico Matemática 10mo grado y que puede ser consultada por el interesado. Dicha demostración puede ser reforzada con el uso de la Rosa, si se tiene en cuenta que: Fig. 1

    Para todo α (0º < α < 90º) siempre es posible encontrar un triángulo ABC rectángulo en C, donde el cateto opuesto a a está contenido en la escala (4) y el cateto adyacente está contenido en la escala (1), correspondientes al seno y coseno respectivamente. En tales condiciones se cumple por el Teorema de Pitágoras:

Ejemplo 3. Analizar las propiedades de la función y = sen x.

    Por la cantidad de propiedades el análisis se limita a algunas de ellas, el resto quedan a consideración del interesado. De otra parte se sugiere ver el procedimiento establecido para estos casos en el libro de texto Matemática 10mo grado, así se prioriza el procedimiento con el medio de enseñanza que es el propósito fundamental.

Monotonía en el primer cuadrante

    En este caso como el seno del ángulo depende del valor de la ordenada de cada punto de la circunferencia, se procede tal como se explica a continuación (en la versión digital o portátil se hace clic en los botones 00 y 900, ubicación que puede observarse también en la figura 1)

• Partir de la posición inicial en 00.

• Girar el radio móvil en sentido positivo, de manera continua hasta 900. Observe cómo durante este movimiento las ordenadas varían de menor a mayor mientras las amplitudes de los ángulos varían en igual sentido, desde 0 hasta1 en el intervalo [0°; 90°].

• Concluir que es monótona creciente.

Ceros

    Por definición son los valores de x, para los cuales f(x) = 0. Si se rota el radio tanto en sentido positivo como negativo podemos observar que esta condición se cumple para x = 00 y x = 1800. Además se consideran todos los ángulos coterminales de estos, por lo que queda mejor interpretada la expresión que determina los ceros de esta función. (Fig. 1 o versión digital)

    El resto de las propiedades así como las demás funciones trigonométricas se pueden analizar y concretar con el uso de este medio de enseñanza sin que necesariamente se disponga de los gráficos correspondientes. De esta manera permite justificar desde la circunferencia trigonométrica el origen y comportamiento de las propiedades en cada gráfico.

Ejemplo 4: Aplicación práctica.

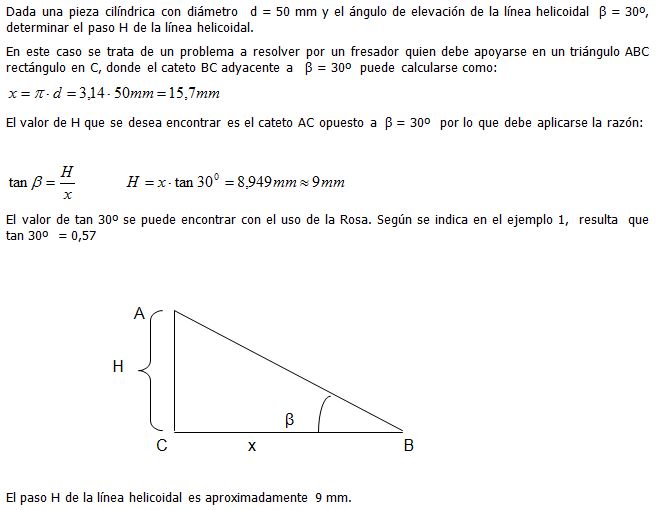
Conclusiones

    Se propone un método de representación dinámica que se materializa con el uso de un medio de enseñaza dinámico como posible solución a las insuficiencias que se revelan en la comprensión de propiedades de las funciones trigonométricas. A partir de dicho método se derivan procedimientos didácticos.

    La Rosa Trigonométrica deviene en uno de esos medios, esencial en la instrumentación de los procedimientos por parte de los alumnos y el profesor. Este medio tiene características que lo distinguen de otros existentes y permite imprimir una dinámica al proceso de visualización de las propiedades de las funciones trigonométricas.

Referencias bibliografías

• Campistrous Pérez, L. et al. Matemática. Décimo grado. Ciudad de La Habana. Editorial Pueblo y Educación, 1989. 347 p.

• Deslis Mendoza, Angel. Importante innovación de profesor caimanerense. Guantánamo. Publicado en línea en Archivo de noticias, Página Web, Biblioteca Municipal “Doris Aguiar Oliveros”, Caimanera, octubre 2008. Disponible en: http://www.gtmo.cult.cu/bibliotecas/bmdaguiar/index.php

• Deslis Mendoza, Angel. La Rosa trigonométrica como medio para la enseñanza de la Trigonometría en la educación preuniversitaria. Holguín. Publicado en el II Taller Nacional de Proyectos de Investigación, ISP José de la Luz y Caballero, 2008. 15 p.

• Deslis Mendoza, Angel. La Rosa trigonométrica y sus complementos. Ponencia presentada en el VI Forum Provincial de Piezas de Repuesto y Tecnologías de Avanzada, Guantánamo, Cuba, 1991. 19 p.

• Deslis Mendoza, Angel. Medio para la enseñanza de la trigonometría elemental. Ciudad de La Habana. Registrado como invención en Oficina Nacional de Invenciones Información Técnica y Marcas, 1994. 10p.

• Deslis Mendoza, Angel; San Juan Azze, Beatriz. Las representaciones dinámicas como formas de visualización de funciones matemáticas. EFDeportes.com, Revista Digital. Buenos Aires, Nº 186, noviembre 2013. ISSN 1514-3465, 7p. http://www.efdeportes.com/efd186/representaciones-dinamicas-de-funciones-matematicas.htm

Otros artículos sobre Educación Física

	Búsqueda personalizada
EFDeportes.com, Revista Digital · Año 18 · N° 190 | Buenos Aires, Marzo de 2014 © 1997-2014 Derechos reservados