Estudio de los límites del ser humano mediante los  resultados de los récords en las pruebas de atletismo Study of the limits of human beings using the results of track records
	*Profesor de secundaria de FQ, Madrid **Profesor de secundaria de Matemáticas, Madrid (España)	Santiago Jiménez Plaza* sjplaza@gmail.com Juan Jesús Tébar Moreno** jj.tebar@gmail.com
	Resumen           En este trabajo se estudian los récords mundiales de atletismo tanto para hombres como para mujeres que llevan estabilizados desde hace mucho tiempo y por tanto nos indican que estamos cercanos a los límites del ser humano. Mediante técnicas matemáticas con polinomios de Lagrange obtenemos los límites actuales para cualquier distancia, aunque no sea olímpica.           Palabras clave: Récords. Atletismo. Límites del ser humano. Polinomios de Lagrange.   Abstract           In this paper we study athletics world’s records for both men and women which have been long stabilized and therefore indicate that we are close to the limits of human beings. Using mathematical techniques with Lagrange polynomials we obtain the current stated limits for any distance, although not Olympic.           Keywords: Records. Track records. Limits. Lagrange polynomials.
	EFDeportes.com, Revista Digital. Buenos Aires, Año 18, Nº 187, Diciembre de 2013. http://www.efdeportes.com/

1 / 1

Introducción

    Citius, altius, fortius (más lejos, mas alto, más fuerte) es el lema del movimiento olímpico desde sus comienzos con el Barón de Coubertin, pero las pruebas clásicas del atletismo llevan tiempo dando muestras de agotamiento (Etayo, 2000), el ejemplo más cercano lo tenemos en los últimos Juegos Olímpicos de Londres, donde sólo se ha batido una marca individual de atletismo: los 800 metros masculinos. Un buen ejemplo de este agotamiento es el resultado de las pruebas de velocidad femenina que superaron en 4 décimas el record mundial.

    Por tanto, queda claro que cada vez es más difícil batir los record mundiales individuales, es por eso que en este trabajo partimos de la hipótesis de estar próximos a los límites del ser humano en el atletismo. El objetivo del presente trabajo es tratar de calcular los límites de rendimiento en cualquier prueba de carrera a través de métodos matemáticos.

Método

    En nuestro caso P(x) = t, el tiempo empleado en el recorrido de la prueba y se han obtenido cuatro polinomios, para las pruebas de velocidad y para las pruebas de resistencia, utilizando el programa MATLAB 7.0 para la obtención de los coeficientes de los polinomios. Para la representación gráfica se ha utilizado el programa GEOGEBRA 4.2. Con los polinomios obtenidos a partir de las marcas mundiales homologadas en las distintas pruebas olímpicas, 2 de velocidad y 2 de resistencia. Las pruebas de velocidad suelen establecerse hasta los 400 m. El principal motivo para dividir el estudio en resistencia y velocidad es porque claramente son dos capacidades distintas que se entrenan de distinta forma y por lo tanto no son comparables.

    La metodología seguida es la siguiente, en un principio se ha hecho una tabla con las distancias de cada prueba y el record correspondiente a dicha prueba. De aquí obtenemos los datos pertinentes para los polinomios de: velocidad en hombres, velocidad en mujeres, resistencia en mujeres y resistencia en hombres. Estos datos los hemos introducido en un programa hecho con MATLAB 7.0, el cual nos devuelve los coeficientes del polinomio interpolador de dichos datos, es decir, el polinomio óptimo hasta el momento. Estos datos los transcribimos en forma de polinomio a GEOGEBRA 4.2 para obtener su representación y así poder obtener conclusiones tanto aritméticas como visuales.

Tabla 1. Records mundiales (www.iaaf.org)

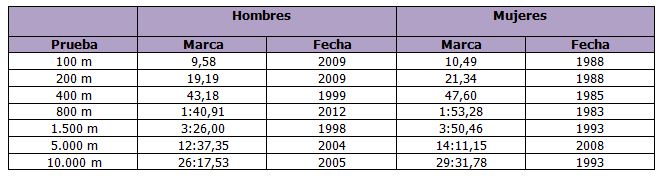
Resultados

    La primera gráfica se obtiene con los datos de las pruebas masculinas en 100m, 200m, 400m y 800m y sus correspondientes records mundiales. Normalmente se consideran pruebas de velocidad hasta los 400 m tanto para hombres como para mujeres, en este estudio hemos ampliado la gráfica de velocidad con el dato de 800 m para conectar ambas gráficas, la de resistencia y la de velocidad.

Gráfica masculinas

Gráfica 1. Velocidad en hombres

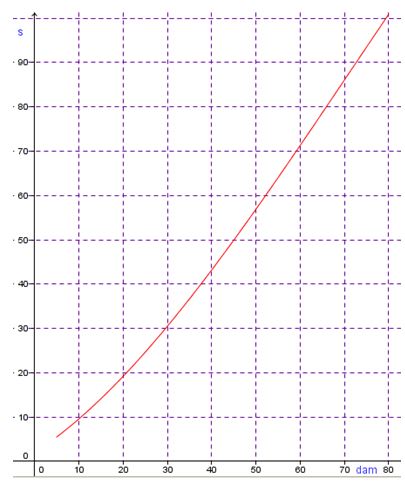
*En la gráfica se representa la distancia en decámetros (dam) en el eje de abscisas y el tiempo en segundos(s) en el eje de ordenadas.

    En la siguiente gráfica se puede observar la representación de los polinomios de Lagrange obtenidos a partir de los datos de resistencia en hombres:

Gráfica 2. Resistencia en hombres

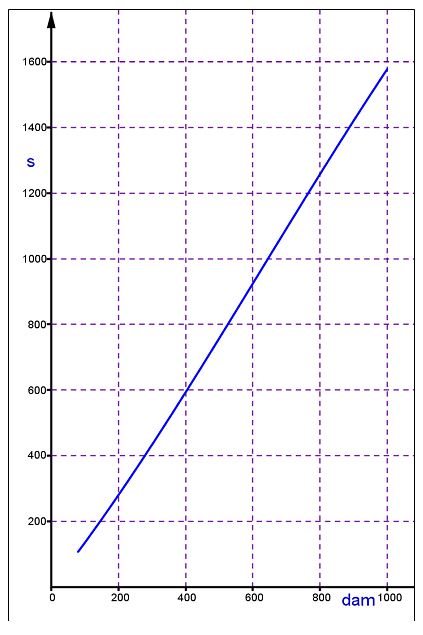
*En la gráfica se representa la distancia en decámetros (dam) en el eje de abscisas y el tiempo en segundos(s) en el eje de ordenadas.

Gráficas femeninas

    Esta gráfica es la representación del polinomio de Lagrange obtenido a partir de los datos de velocidad en mujeres:

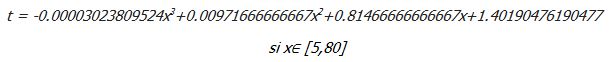
Gráfica 3. Velocidad en mujeres

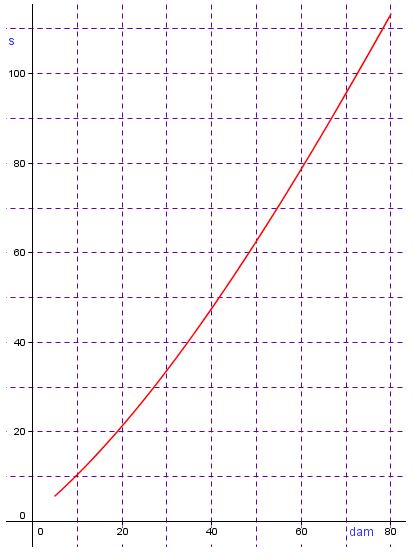
*En la gráfica se representa la distancia en decámetros (dam) en el eje de abscisas y el tiempo en segundos(s) en el eje de ordenadas.

 

Gráfica 4. Resistencia en mujeres

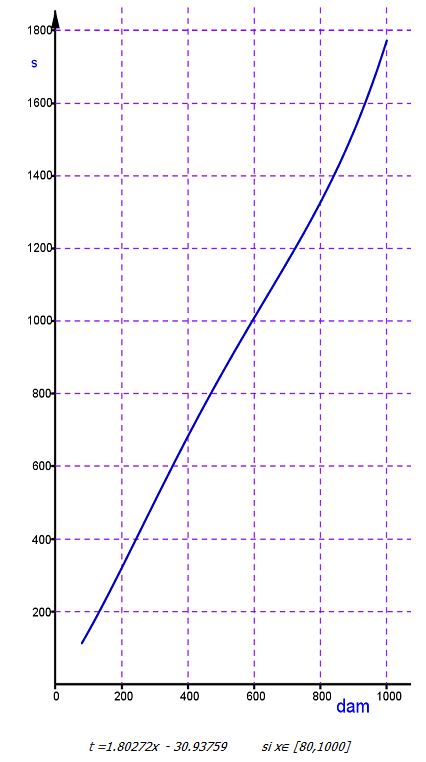
*En la gráfica se representa la distancia en decámetros (dam) en el eje de abscisas y el tiempo en segundos(s) en el eje de ordenadas.

    Esta gráfica es la representación de los polinomios de Lagrange obtenidos a partir de los datos de resistencia en mujeres:

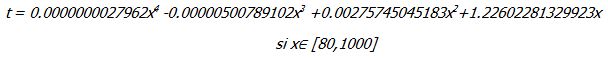
Discusión

    La principal utilidad del presente trabajo consiste en calcular la plusmarca mundial teórica de cualquier distancia, aunque no sea prueba oficial olímpica. Por ejemplo en una prueba de 300 m para los hombres en la curva de velocidad hasta 400 m, nuestro método nos proporciona una plusmarca mundial de 30,5 s. Es lo que podríamos esperar de atletas específicamente entrenados para esta prueba que no es olímpica. En la misma línea, pero con métodos estadísticos se obtienen resultados de marcas esperadas. (Radicci, 2012)

    En la tabla 3 pueden verse algunas predicciones de marcas mundiales de distancias corridas por deportistas masculinas de élite, pero no olímpicas.

Tabla 3. Resultados esperados según nuestros polinomios en comparación con los obtenidos por los atletas en dichas pruebas

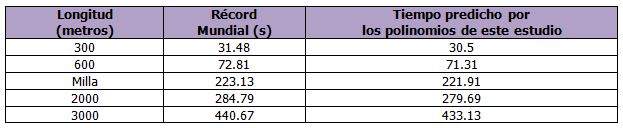
    Como podemos observar en la Tabla 3, los valores predichos por los polinomios tienen relación con los obtenidos por los atletas. Son sensiblemente inferiores porque los atletas no entrenan específicamente para dichas distancias, de aquí se puede deducir que si lo hicieran podrían alcanzar dichos valores.

    Para pruebas de resistencia se puede deducir que hay una velocidad que se mantiene durante bastante tiempo, de acuerdo con ecuaciones de la dinámica (Hernández Gómez, 2013).

Conclusiones

    En primer lugar no hay convergencia a grandes distancias entre hombres y mujeres.

    Al haber utilizado datos de marcas mundiales, obviamente los polinomios nos dan una relación de hacia donde tienden nuestros límites y la marca a la que podría tender un deportista si decide preparar una prueba. Dependiendo de la cercanía de su marca al polinomio, podría determinarse el valor real de dicha marca.

    Para deportistas aficionados que no estén en la élite, que tengan marcas en distintas pruebas, utilizando nuestro programa podemos obtener su polinomio a medida, para que pueda ver cual serían sus marcas en otras pruebas e incluso su prueba óptima; siempre atendiendo a la distinción esencial entre velocidad y resistencia.

    Para encontrar la prueba más veloz (óptima) que un atleta (en este caso masculino) podría correr, tomando la ecuación del ajuste (considerando los nodos de 100, 200 y 400 metros) en velocidad: t = 0,00795x² + 0,7225x + 1,56; donde t está en segundos(s) y x en decámetros (dam). Formamos la función, velocidad media de la trayectoria x/t y buscamos su valor máximo con ayuda de su derivada primera respecto a x, resolviendo aparece un valor de x = 14,008 dam y un tiempo de 13 s y 24 centésimas de segundo. La segunda derivada de esta función, demuestra que es un mínimo. Lo que significa que de acuerdo con las marcas actuales, la distancia que un plusmarquista recorrería a mayor velocidad es 140 m. Tal vez podría pensarse en incluir más a menudo pruebas de 150 m (la más cercana a la distancia ideal) que pudieran resultar muy vistosas según los datos obtenidos.

    Para las mujeres, considerando t = 0,0076x² + 0,857x + 1,16; donde t está en segundos(s) y x en decámetros (dam). Por el mismo procedimiento que en el caso de los hombres y resolviendo del mismo modo aparece un valor de x = 12,35 dam y un tiempo de 12 s y 90 centésimas de s. La segunda derivada de esta función, demuestra que es un mínimo. Lo que significa que de acuerdo con las marcas actuales, la distancia que una plusmarquista recorrería a mayor velocidad es de 123,5 m.

Referencias

• Etayo Gordejuela, J.J. (2000) Los límites humanos: la evolución de las mejores marcas mundiales del atletismo. Arbor CLXV, 650 (Febrero 2000), 289-317 pp.

• Hernández Gómez, J.J. On the performance of Usain Bolt in the 100 m sprint. Eur. J. Phys. 34 1227 (25 Jul 2013).

• Radicchi Filippo. Universality, Limits and Predictability of Gold Performances at the Olympic Games. (12 Jul 2012). PLOS ONE.

Otros artículos sobre Atletismo

	Búsqueda personalizada
EFDeportes.com, Revista Digital · Año 18 · N° 187 | Buenos Aires, Diciembre de 2013 © 1997-2013 Derechos reservados