Introducción
En el ámbito de la investigación, a partir del análisis teórico y práctico
del aparato visto de la metodología como ciencia, se infiere que no siempre lo
que constituye una regularidad, existe en una relación adecuada entre métodos,
procedimientos y medios. Al describir el método de representaciones, se emplean
medios que no posibilitan la visualización inmediata de variaciones en
determinadas relaciones.
Los métodos y procedimientos referidos no favorecen la comprensión ni la
generalización como habilidades esenciales en la apropiación del conocimiento.
Por otra parte, con el desarrollo de las tecnologías y la comunicación, surgen
aplicaciones que se emplean como medios en el proceso de enseñanza-aprendizaje
de la trigonometría. Estas aplicaciones ofrecen referentes variables en corto
tiempo; pero no se describe el método que sustente de manera adecuada el uso de
estos medios.
En correspondencia con este análisis teórico-práctico se revela la necesidad
de formular un método que genere una dinámica favorable para la apropiación
de las propiedades de las funciones trigonométricas en el proceso de
enseñanza-aprendizaje de las matemáticas en la educación preuniversitaria.
Además la necesidad de aportar en un método de representación radica en que
es la posible solución a las insuficiencias que se revelan con la aplicación
de métodos empíricos y teóricos.
Este autor propone un método de representación dinámica para favorecer la
comprensión de las propiedades de las funciones trigonométricas en la
educación preuniversitaria. Dicho método se fundamenta en la
contextualización de un sistema de principios didácticos. Este sistema tiene
como componente jerárquico, el principio de visualización.
Materiales y
métodos
Para la elaboración de este artículo se emplean como materiales las
bibliografías que se corresponden con el tema y que fundamentan desde la
teoría los argumentos que se exponen. Entre los métodos se utilizan
entrevistas, observaciones participantes y registros de experiencias donde se
presenta la relatoría de la aplicación del método de representación
dinámica como forma de visualización matemática en el proceso de
enseñanza-aprendizaje de la trigonometría
Resultados del
trabajo
Las representaciones, en el proceso de enseñanza-aprendizaje de la Matemática,
suelen emplearse en forma estática o dinámica. La forma estática es la que
más se utiliza, en tanto la forma dinámica es la menos vista. Ambas
representaciones constituyen formas de visualización.
La visualización como principio de la Psicología y la Didáctica se fundamenta
en las leyes que direccionan el desarrollo correlativo de la abstracción, la
generalización y la concreción en los estudiantes. Permite emplear el
conocimiento sensorial, acumular ideas sobre objetos y fenómenos concretos, con
la finalidad de obtener conocimientos teóricos generalizados y perfeccionarlos.
En el proceso de enseñanza-aprendizaje de la geometría y la trigonometría, en
particular de las funciones trigonométricas, se requiere de la visualización.
Con esta se activan, estimulan y desarrollan los procesos lógicos del
pensamiento para obtener el nuevo conocimiento. Además permite al alumno
reflexionar, profundizar, definir, valorar, argumentar y conjeturar.
La visualización facilita el aprendizaje de conceptos básicos trigonométricos
y sus aplicaciones a situaciones de aprendizaje y a la resolución de problemas.
Por otra parte permite exigir del alumno la búsqueda y exploración de
relaciones, propiedades y formas de representación de las funciones
trigonométricas, aún sin la presencia de sus gráficos.
Se contextualizan los principios didácticos de la comprensión, de la solidez
de la asimilación de los conocimientos y de visualización. Estos principios
interactúan entre sí en relaciones de subordinación y de coordinación. En
particular, del principio de visualización se deriva un método de
representación dinámica para favorecer la comprensión de las propiedades de
las funciones trigonométricas.
Respecto a la concepción del método de enseñanza y de aprendizaje se acopian
criterios de algunos autores. De estos autores se tienen en cuenta los criterios
de KLINGBERG y col. (1973), DANILOV y SKATKIN (1978) y BERMÚDEZ y RODRÍGUEZ
(1996). Según criterios de KLINGBERG y col. (1973), el método de enseñanza es
el camino que sigue el maestro para dirigir y controlar el proceso de
aprendizaje o, lo que es lo mismo, el proceso planificado y sistemático de
apropiación de la materia de enseñanza. A manera de complementar la
definición, los autores precisan además:
-
El método
de enseñanza es también una forma de servir de mediador entre los alumnos
y la materia de enseñanza.
-
El nexo
entre método de enseñanza y método científico es el aspecto lógico del
primero.
-
Los
métodos de enseñanza además de estar determinados por factores lógicos,
están determinados por factores psicológicos.
DANILOV y SKATKIN (1978) consideran que todo método es un sistema de acciones
sucesivas y conscientes del hombre, que tiende a alcanzar un resultado que
corresponde al objetivo trazado. En tal aspecto, respecto a la relación
existente entre método y fin (objetivo), dichos autores plantean que si el fin
no es alcanzado, el método fue, por consiguiente, inadecuado para el fin
perseguido, o sea, es incorrectamente trazado o el método incorrectamente
aplicado.
Según lo investigado, de los principios didácticos, se derivan en el plano
teórico y en el plano práctico los métodos, los procedimientos y los medios
de enseñanza. El método es considerado como categoría metodológica rectora.
Así se define, según la etimología de la palabra, en BERMÚDEZ y RODRÍGUEZ
(1996), como el camino del pensamiento humano para alcanzar un determinado
objetivo de su conocimiento o modo de reproducir lo estudiado.
Los autores referidos, realizan un análisis sobre la estructura y
funcionamiento del método. Además plantean como premisas: la finalidad
en la creación del método, la elaboración, el uso, la relación de lo
objetivo y lo subjetivo; y la relación de lo interno y lo externo.
Cuando se habla de método, se está en presencia de una representación
abstracta para el logro de un fin determinado. En tal sentido, es el maestro
quien se vale de este para tal logro. Sin embargo, no es correcto pensar que con
el método presentado por el maestro, el alumno logre su instrumentación en el
plano práctico-metodológico.
Por estas razones, del método se derivan tanto los procedimientos como los
medios. Estos a su vez, constituyen en la práctica el modo de instrumentación
del método para que el alumno logre el objetivo propuesto. Según BERMÚDEZ y
RODRÍGUEZ (1996), el método es la categoría metodológica rectora y los
procedimientos y medios, categorías subordinadas a éste.
Desde el punto de vista filosófico, el conocimiento racional exige la
trascendencia del nivel contemplativo, a un nivel superior aplicativo. Esto se
corresponde con el camino dialéctico que recorre el conocimiento planteado por
Lenin quien apuntaba: “…De la contemplación
viva al pensamiento abstracto y de éste a la práctica”.
En el nivel aplicativo, se reconoce el establecimiento de relaciones por parte
del sujeto que aplica. De otra parte, se reconoce la reestructuración de la
experiencia personal de carácter cognitiva y/o instrumental. Además, la
aplicación puede estar dirigida a producir o reproducir algo.
Atendiendo a los niveles de aplicación, los métodos se consideran como
reproductivos y productivos. La aplicación reproductiva, se manifiesta cuando
la situación planteada es nueva y el alumno reproduce procedimientos ya
elaborados. En tanto la aplicación productiva requiere de la construcción, por
parte del sujeto, de los procedimientos empleados.
En muchas clasificaciones de los métodos de enseñanza, se observa que están
desprovistas de los procedimientos que permitan su instrumentación. Esto trae
como consecuencia, la existencia de divergencias en criterios asumidos para la
determinación del contenido de los métodos.
Según estos autores, la finalidad del método, pudiese ser un criterio lícito
y confiable en la diferenciación de un método respecto a otro. De esta manera,
los métodos de aprendizaje pueden diferenciarse en métodos reproductivos y
métodos productivos, en dependencia de la finalidad que el alumno persigue con
la utilización del método.
El método de representación dinámica tiene sus antecedentes según CASANO
(2008), en la ingeniería civil respecto al análisis de estructuras bajo
acciones dinámicas. Por otra parte según GAMBOA (2007), en el uso de las
tecnologías en la enseñanza de la matemática, a partir de la creación de
software dinámicos. En este contexto, se restringe lo que representa una
dinámica, puesto que se explicitan sólo la representación del concepto como
tablas y gráficos obtenidos posterior a la introducción de determinados
parámetros.
Para este autor, en una representación dinámica como método, en el ámbito de
las funciones trigonométricas; el alumno debe visualizar una variedad de
relaciones antes de interactuar con el contenido. Tales relaciones deben
desentrañar el origen de las funciones trigonométricas desde la circunferencia
trigonométrica, las que favorecen la puesta en práctica de una serie de
razonamientos que permitan resolver situaciones de aprendizaje.
Para los intereses de esta investigación, el método de representación
dinámica tiene como bases para su instrumentación, el procedimiento de la
visualización por un lado y un procedimiento general heurístico, de otra
parte. La visualización es entendida tanto procedimiento como principio y
método.
En la rama de la Geometría, se emplean representaciones geométricas básicas
como el punto, la recta y el plano con el propósito de visualizar objetos de la
realidad. Además es posible la representación de estos elementos básicos y
sus combinaciones en un sistema de coordenadas cartesianas.
Las funciones matemáticas en general, son representaciones simbólicas que
reflejan el comportamiento de fenómenos físicos de la realidad. A cada
función se le asocia una representación gráfica de lo visual en ese fenómeno
y permite el análisis del comportamiento de las propiedades.
Aún así, se revelan insuficiencias en la comprensión de las propiedades de
funciones. En este sentido se propone considerar un sistema de medios de
enseñanza que fortalezcan el proceso de visualización, en un nivel que exige
del estudiante mayor abstracción y generalización.
Resulta necesario definir las nuevas categorías que se introducen. Como
resultado de la sistematización de las definiciones tratadas por otros autores,
se considera:
-
Representación:
la imagen de un objeto o fenómeno de la realidad, expresada mediante
palabras o símbolos, como resultado de la producción y conservación en la
conciencia del hombre. La representación existe como forma de abstracción
y es independiente de la existencia real del objeto o fenómeno.
-
Representación
dinámica: aquella representación que posee o se le imprime un movimiento,
que provoca un cambio de posición del objeto o fenómeno representado
respecto a su posición inicial.
-
Método: el
camino o la vía de la cual se apropia el sujeto para alcanzar un
determinado objetivo de su conocimiento, o modo de reproducir el objeto
estudiado en el pensamiento.
-
Método de
enseñanza: el camino o la vía que sigue el maestro para lograr un objetivo
determinado en el proceso de enseñanza, que puede ser aplicable en una o
varias asignaturas afines.
-
Método de
representación dinámica de la relación gráfico-propiedades de las
funciones trigonométricas: el método de enseñanza que emplea el maestro
para favorecer el aprendizaje de contenidos básicos trigonométricos, a
partir de la visualización de las variaciones en el objeto matemático en
el espacio y el tiempo; que puede incidir en el desarrollo de procesos
lógicos del pensamiento, al resolver tareas en el ámbito del estudio de
estas funciones.
El objeto matemático que refiere la definición, a consideración del autor lo
conforman las funciones trigonométricas. Es en estas funciones donde aún
persisten las insuficiencias respecto a la comprensión de sus propiedades. De
tal manera, queda explícito el fin del método: el aprendizaje de los
contenidos concernientes a funciones trigonométricas y una vez más se
revela la estrecha relación entre enseñanza y aprendizaje.
A partir del método es posible derivar tanto los procedimientos como los
medios. Estos a su vez, concretan en la práctica la implementación del
método, en particular el método de representación dinámica. Como sistema de
procedimientos que se manifiestan en la práctica se asume el conformado por el
de visualización y el general heurístico. Ambos procedimientos, según el
criterio de otros autores, son al propio tiempo métodos y/o principios de la
didáctica.
El procedimiento general heurístico permite conjeturar sobre el comportamiento
de propiedades de las funciones trigonométricas. En este caso, se puede
accionar con ayuda de las representaciones gráficas estáticas y también con
el uso de los medios dinámicos derivados del método de representación
dinámica.
En Conferencias sobre metodología de la enseñanza de la matemática (JUNK,
1979) aparece una conferencia dedicada al tratamiento de las clases de
funciones. Además, se expone de manera clara que el objetivo esencial es que el
alumno sea capaz de representar gráficamente las funciones y encontrar las
características de funciones de determinadas clases.
En el material aparecen sucesiones de indicaciones algorítmicas para el
tratamiento de diferentes funciones. Estas indicaciones sirven como modelo para
las sucesiones de indicaciones contenidas en el procedimiento general
heurístico que se pretende introducir durante el proceso de
enseñanza-aprendizaje de las funciones trigonométricas.
En particular se pretende establecer un procedimiento general heurístico que
permita el descubrimiento, por parte del propio alumno, de la existencia de la
relación entre el gráfico y las propiedades de las funciones trigonométricas.
Tal procedimiento se constituye en un proceso analítico que prevé una vía
deductiva y otra inductiva para el análisis de cada propiedad.
Lo expuesto por PÉREZ y col. (1989) en Metodología de la Investigación
Educativa puede ser útil para esclarecer el procedimiento heurístico que se
pretende introducir. Tales autores respecto al método inductivo-deductivo,
ofrecen las definiciones siguientes:
-
Inducción:
Forma de razonamiento por medio del cual se pasa del conocimiento de casos
particulares a un conocimiento más general que refleja lo que hay de común
en los fenómenos individuales. En este método se pone de manifiesto la
relación de lo particular a lo general como categoría filosófica.
-
Deducción:
Forma de razonamiento mediante el cual se pasa de un conocimiento general a
otro de menor nivel de generalidad. El razonamiento deductivo toma como
premisa el conocimiento de lo general y es así como nos puede llevar a
comprender lo particular, en el que existe lo general.
La inducción y la deducción se complementan mutuamente durante el proceso de
desarrollo del conocimiento. Al respecto se plantea que el papel de la
inducción y la deducción en el conocimiento se explica por el enlace objetivo
de lo singular y lo general en la realidad misma, por las modificaciones de
tales contrarios al transformarse unos en otros.
El procedimiento en sí mismo contiene una sucesión de indicaciones para cada
vía considerada. A causa de la variedad de funciones por una parte y de
propiedades por la otra, la sucesión de indicaciones no resulta coincidente
para todas las propiedades que se analicen. Por este motivo el procedimiento no
es algorítmico.
A modo de ejemplo, se describen las sucesiones de indicaciones para el análisis
de la propiedad referida a la paridad de la función coseno y su relación con
el gráfico. Además se propone el análisis apoyado en un medio de enseñanza
no tradicional propuesto por el autor que dinamiza y visualiza el análisis de
propiedades en el proceso de enseñanza-aprendizaje.
Ejemplo 1.
Análisis de la paridad de la función coseno
Sucesión de
indicaciones
I Vía
deductiva
-
Orientación
sobre el concepto de paridad que aparece para poder identificar la
propiedad.
-
Expresarlo
en forma simbólica : f (x) = f (-x)
-
Evaluar
para casos particulares
-
Comparar
resultados
-
Arribar a
conclusiones
-
Construir
el esbozo del gráfico de la función analizada
II Vía
inductiva:
-
A partir
de gráficos conocidos, trazar en cada uno, una recta paralela al eje X
que corte a dichos gráficos.
-
Comprobar
si existen puntos de intersección entre el gráfico y la recta trazada,
que sean simétricos respecto al eje Y.
-
Comparar
las alturas de estos puntos y decidir si están o no, en un mismo
semiplano.
-
Arribar a
conclusiones
-
Identificar
el tipo de paridad
-
Decidir
si el gráfico de la función coseno es par
Las sucesiones de indicaciones presentadas en cada vía utilizada se
corresponden con las definiciones dadas para la inducción y la deducción. En
consecuencia se evidencia en los planos teórico y práctico, la relación
dialéctica entre lo singular y lo general en su doble sentido.
Respecto al medio de enseñanza no tradicional, se propone su uso para el
análisis de la paridad de la función coseno, mediante una sucesión de
indicaciones.
I Vía
inductiva:
-
Orientación
sobre el concepto de paridad para identificar la propiedad.
-
Expresarlo
en forma simbólica
-
Evaluar
para casos particulares, preferentemente en ángulos notables.
En esta indicación se puede escoger por ejemplo: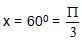 
y su simétrico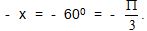 
Al observar en el medio de enseñanza, el alumno debe percatarse que estos
valores son simétricos respecto al eje X y la cuerda determinada por los puntos
de intersección con la circunferencia, corta a la escala del coseno en
exactamente la mitad, entonces:
Durante el análisis de la función coseno, a
diferencia de la función seno; en el círculo trigonométrico los ejes
coordenados y el círculo rotan 90° en sentido positivo por lo que dichos ejes
se intercambian.
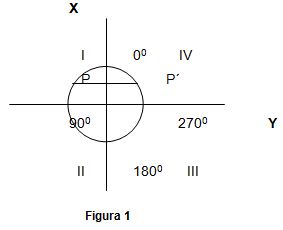
Como resultado de la rotación de los ejes, P y P´ son simétricos respecto al
eje X. Cuando se analiza la simetría del gráfico para la función coseno en el
sistema de coordenadas convencional, se refiere al eje Y como eje de simetría.
Por esta razón se genera una contradicción evidente respecto a lo que se
analiza cuando se emplea el medio propuesto.
Para la función coseno, el simétrico de un ángulo del I Cuadrante está en el
IV Cuadrante y el coseno de éste es también positivo. De manera que el orden
de los cuadrantes para esta función en el sistema de coordenadas es según la
sucesión: …IV, I, II, III…
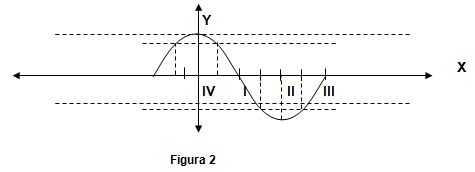
El gráfico correspondiente a la función coseno es simétrico respecto al eje X
y no al eje Y. Estas consideraciones pueden servir para la reflexión de los
docentes que imparten trigonometría en la educación preuniversitaria.
Esta investigación emplea como formas prácticas de visualización, medios de
enseñanza elaborados por el autor y medios existentes en las nuevas
tecnologías. Dichos medios cumplen en el proceso de enseñanza-aprendizaje las
funciones pedagógicas, filosóficas y psicológicas.
El sistema medios de enseñanza que propone el autor lo conforman: la Rosa
trigonométrica como medio jerárquico no tradicional dada la multiplicidad de
posibilidades de empleo en la unidad trigonometría, la plantilla múltiple para
el trazado de funciones trigonométricas normales y el curvígrafo rústico para
el trazado cualquier función trigonométrica a partir del ploteo de puntos.
Como medios existentes en las nuevas tecnologías, se pueden emplear durante el
trabajo independiente los simuladores de los gráficos de las funciones
trigonométricas. Además se puede utilizar una simulación en flash de la Rosa
trigonométrica.
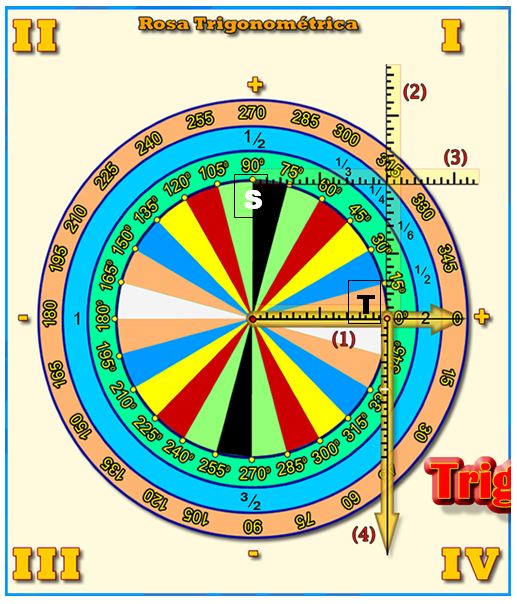
La Rosa Trigonométrica se
considera como medio jerárquico en este sistema por sus múltiples aplicaciones
en el transcurso de toda la sub unidad. Además con la Rosa es posible el
cálculo de valores trigonométricos que permiten la ubicación de los puntos
pertenecientes a una función en el sistema de coordenadas. De esta manera, es
posible la construcción de la plantilla para funciones trigonométricas
normales con el uso del curvígrafo.
El curvígrafo facilita el trazado de cualquier función trigonométrica a
partir del ploteo de puntos. La Rosa también permite el análisis de las
propiedades de estas funciones y además, fundamentar el comportamiento de
éstas en el gráfico correspondiente. La nueva tecnología permite la
simulación de gráficos a partir de parámetros establecidos.
Ventajas
del medio no tradicional (la Rosa Trigonométrica)
-
Es
un medio que puede ser construido tanto por los alumnos como por los
docentes, con materiales de bajo costo.
-
Puede
ser empleado en su forma natural en las clases de trigonometría y en su
forma digitalizada como flash en los laboratorios de computación.
-
Sirve
como complemento para las clases presenciales en ausencia de las nuevas
tecnologías.
-
Es
un medio que puede ser manipulado por alumnos y docentes de manera tal que
el alumno se convierte en agente activo de su propio conocimiento.
-
Debido
a sus características distintivas, puede ser empleado durante la
retroalimentación y sistematización de los contenidos trigonométricos que
preceden a las funciones trigonométricas, en el desarrollo de los
contenidos sobre funciones trigonométricas y en la sistematización general
de estos conocimientos dentro y fuera del ámbito de la clase.
-
Permite
la modelación y visualización de las propiedades de las funciones
trigonométricas según las variaciones de las posiciones de puntos en la
circunferencia trigonométrica.
El sistema de procedimientos y medios de enseñanza dinámicos, permiten
dinamizar el método de representación propuesto. El accionar de estos y su
interrelación favorece en la práctica, la comprensión de las propiedades de
las funciones trigonométricas.
La Rosa Trigonométrica, creada por el autor en 1991 y diseñada por el técnico
en computación Magdiel González (2007)
Bibliografía
-
Bermúdez,
Rogelio y Rodríguez, M. (1996). Teoría y metodología del aprendizaje.
Editorial Pueblo y Educación. Ciudad de La Habana. Cuba, págs. 21-35
Casano,
A. M. (2008). Análisis de estructuras bajo acciones dinámicas.
Disponible en http://www.edutecn.utm.edu.ar/guias_de_estudio/estruc_dinam.pdf
Deslis, Angel
(1994). Medio para la enseñanza de la trigonometría elemental.
Registrado en Oficina Nacional de Invenciones Información Técnica y Marcas.
Ciudad de La Habana. Cuba.
____________
(2008). Importante innovación de profesor caimanerense. Guantánamo,
Cuba. Disponible en: Archivo de noticias, octubre.
http://www.gtmo.cult.cu/bibliotecas/bmdaguiar/index.php
_____________
(2008). La Rosa trigonométrica como medio para la enseñanza de la
Trigonometría en la educación preuniversitaria. Publicado en el II
Taller Nacional de Proyectos de Investigación, ISP José de la Luz y
Caballero. Holguín.Cuba.
Gamboa,
K. (2007). Uso de las tecnologías en la enseñanza de la matemática.
Disponible en: http://www.cimm.ucr.ac.cr/cuadernos/cuaderno3/cuaderno3_c1.pdf
(Fecha de acceso: 23-03-2013)
Klingberg,
Lothar ; Paul, Hans-Georg; Wenge, Horst y Winke, Gunter (1978).
Introducción a la Didáctica General. Editorial Progreso. Moscú, pág.
28, 29.
Pérez,
Gastón; Nacedo de León, Irma y García, Miriam (1996). Metodología de la
Investigación Educacional. Primera parte. Pueblo y Educación. Ciudad de
La Habana. Cuba, pág. 72, 73.
Rodríguez,
Flor; Montiel, Gisela y Cantoral, Ricardo. (2008). Visualization in
Iterative Processes. Centro de Educación en Matemática Educativa.
Universidad Autónoma de Guerrero. México. Material digitalizado en inglés,
págs. 1-9.
Schoenwald,
Justin (1984). Trigonometry visualizer and Method of making same.
Registrado en Oficina Nacional de Invenciones Información Técnica y Marcas.
Ciudad de La Habana. Cuba.
Otros artículos sobre
Educación Física
 |
|
|
EFDeportes.com, Revista
Digital · Año 18 · N° 186 | Buenos Aires,
Noviembre de 2013
© 1997-2013 Derechos reservados
|
