La importancia del análisis dinámico del movimiento mecánico para el estudio de los movimientos deportivos, en la asignatura Biomecánica
	Licenciatura en Cultura Física Holguín (Cuba)	MSc. Nelson Manuel Infante Ruiz MSc. Amanda Gómez Zoquez agomez@cultfis.holguin.inf.cu Lic. Orlando Miguel Rodríguez Granado Lic. Ana Mendoza Oliver isnalvis@unoris.hlg.sld.cu
	Resumen           El presente artículo contiene los resultados de una investigación, cuyo punto de partida es la determinación, a través de un estudio diagnóstico, de las insuficiencias que presentan los estudiantes de la carrera de Cultura Física, pertenecientes a la FUM, en la resolución de problemas, utilizando el método dinámico, como base para lograr un adecuado aprendizaje en la asignatura Biomecánica. Con la utilización de los métodos histórico-lógico, analítico-sintético, inductivo-deductivo la encuesta, la entrevista, el enfoque sistemático-estructural-funcional, un diagnóstico de entrada y salida y el criterio de expertos, se cumplió el siguiente objetivo propuesto: la elaboración de una metodología para favorecer el aprendizaje de la Biomecánica, a través de la resolución de problemas. Lo anterior permite homogeneizar la línea metodológica seguida por los docentes de la universalización para la introducción de los métodos de solución de problemas, en el proceso de enseñanza aprendizaje de las asignaturas, estrechamente relacionadas con la Física. Como resultado se encontró que el Enfoque Histórico Cultural, el Aprendizaje Significativo y la Didáctica de la Física contemporánea, permiten sustentar teórica y metodológicamente la propuesta, observándose una tendencia a la pertinencia y efectividad de esta metodología.           Palabras clave: Resolución de problemas. Biomecánica. Método dinámico.
	EFDeportes.com, Revista Digital. Buenos Aires - Año 18 - Nº 182 - Julio de 2013. http://www.efdeportes.com/

1 / 1

Introducción

    La Biomecánica es la ciencia de las leyes del movimiento mecánico en los sistemas vivos.

    En el surgimiento de la Biomecánica, ejerció una influencia decisiva el desarrollo de la Mecánica, en particular, su nueva tendencia surgida desde los tiempos de Galileo (1564-1642) y Newton (1642-1727). Sin embargo, ya Leonardo da Vinci (1452-1519) afirmaba que: “la ciencia de la mecánica era la más útil y generosa de todas las ciencias semejantes, porque resulta que todos los cuerpos vivos que tienen movimiento actúan bajo sus leyes”. (Citado por Donskoi y Zatsiorski). D. Borelli (1608-1679, alumno de Galileo), médico, matemático y físico- estudió los vínculos entre la física y la medicina y sentó las bases de la Biomecánica como rama de la ciencia en su libro Acerca del movimiento de los animales (1679). (Citado por Donskoi y Zatsiorski).

    La Biomecánica Deportiva, como disciplina docente, estudia los movimientos del hombre en el proceso de los ejercicios físicos. En ese análisis se investigan las causas mecánicas y biológicas de los movimientos y las particularidades de las acciones motoras que dependen de ellas en las diferentes condiciones. El movimiento mecánico del hombre, que se estudia en la Biomecánica Deportiva, se produce bajo la acción de las fuerzas mecánicas externas (gravedad, fricción y muchas otras) y de las fuerzas de tracción muscular. Su objeto de estudio y los métodos de trabajo empleados hacen una importante contribución al desarrollo del pensamiento lógico de los estudiantes basado en la ciencia, proporcionándoles conocimientos de universal reconocimiento para el exitoso desarrollo de esta especialidad.

    No obstante todo lo planteado, y el sustento científico del diseño de los programas, aún no se logra que los estudiantes dominen adecuadamente el método dinámico de solución de problemas, lo que trae como consecuencia que no puedan entender conscientemente el por qué de los movimientos en el deporte, ya que los mismos están condicionados por las leyes de la Mecánica.

    Teniendo en cuenta los cambios operados en la Educación Superior, con el surgimiento de la universalización, se efectuó un estudio diagnóstico para constatar el estado actual del aprendizaje de la resolución de problemas en los estudiantes, como base para la asignatura de Biomecánica, en la FUM.

    El mismo consistió en:

• Se aplicó una prueba pedagógica de entrada.

• Se encuestaron 23 estudiantes de la FUM.

• Se entrevistaron a 4 docentes del centro.

    Los elementos anteriores, conjuntamente con la experiencia de los investigadores como docentes, permitieron constatar las siguientes insuficiencias:

1. Escasa solidez en los conocimientos.

2. Pobre desarrollo de habilidades en la resolución de problemas de Mecánica.

3. Pobre desarrollo del pensamiento lógico.

4. Insuficiente dominio por parte de los docentes de la didáctica y la metodología de la enseñanza de la resolución de problemas de Mecánica.

    Las razones anteriormente referidas permitieron declarar el siguiente problema de investigación: Insuficiencias en el aprendizaje de la Biomecánica limitan el proceso de formación del estudiante de Licenciatura en Cultura Física de la FUM.

    De modo tal que el proceso de enseñanza-aprendizaje de la Biomecánica constituye el objeto de investigación. Y como campo de acción: el aprendizaje de la resolución de problemas de Mecánica, en el proceso de formación del estudiante de la FUM.

    Elaborar una metodología para favorecer el aprendizaje de la Biomecánica, a través de la resolución de problemas de Mecánica, constituye el objetivo de la investigación.

La definición de problemas y su proceso de solución

    El tema de la resolución de problemas ha sido ampliamente abordado por Psicólogos y profesores de Matemática. En el contexto de este trabajo se asume el dado por el Dr. C. Joaquín Palacio Peña donde plantea que se considera problema “toda situación en la que hay un planteamiento inicial que es necesario transformar, siendo desconocida la vía para hacerlo, pero que se cuenta con el deseo y los recursos necesarios para buscar las relaciones que contribuyan a su transformación”.

    Los modelos de solución de problemas propuestos por los psicólogos son de carácter general y aplicable a cualquier problema, los mismos proponen cinco fases, que se pueden resumir en las siguientes:

1. Identificación del problema.

2. Definición del problema.

3. Análisis de los recursos disponibles para solucionar el problema.

4. La ejecución del proceso de solución.

5. Evaluación de la solución.

    En el caso de los modelos propuestos por los matemáticos, ya sean generales o particulares como se planteó anteriormente, se observa el establecimiento de cuatro fases para el proceso de solución, las cuales son:

1. Comprender el problema.

2. Elaboración de un plan de solución.

3. Ejecución del plan de solución.

4. Comprobación de la solución.

    Para la elaboración de la metodología, además del análisis de los modelos presentados anteriormente, se tuvieron en cuenta los siguientes presupuestos:

1. El aprendizaje significativo (Ausubel) y la teoría de la actividad (Vigotsky y Leontiev), por lo que significan para la resolución de problemas y la necesidad de la motivación en la realización de los mismos.

2. La interiorización de las acciones mentales y sus implicaciones didácticas. (Galperin).

3. La posibilidad de aprender procedimientos generalizados y por tanto, la necesidad de enseñarlos. (Talizina).

4. Las funciones generalmente reconocidas al trabajo con problemas en la escuela; instructivas, educativas y de desarrollo. (Campistrous y Rizo, Carlos Álvarez).

5. Las fases en la solución de problemas: comprender el problema, búsqueda de la vía de solución, solución y vista retrospectiva y su relación con los momentos de la actividad. (Polya, Shöenfeld, Labarrere, de Guzmán, Campistrous y Rizo).

6. La caracterización de los problemas escolares.

7. La caracterización del comportamiento de los sujetos en el proceso de solución de problemas: los recursos, la heurística, el control y el sistema de creencias. (Shöenfeld, Campistrous y Rizo).

Metodología de resolución de problemas

    La Metodología elaborada, contiene como uno de sus procedimientos esenciales, la corroboración de su factibilidad, la cual se realizó a través del Criterio de Expertos, la aplicación de una prueba pedagógica de salida y la implementación parcial a través de una experiencia pedagógica, comprobándose así su pertinencia y factibilidad. Una representación esquemática de la lógica de desarrollo de la metodología se representa en la siguiente figura.

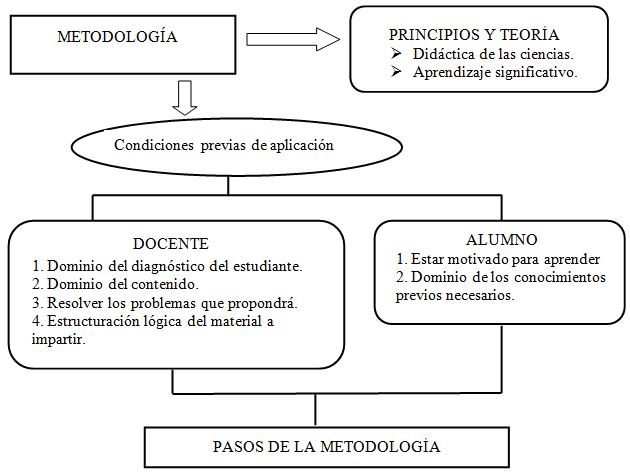
I.     Teoría de aprendizaje y principios sobre los que se sustenta la metodología

    En la base de la conformación de la metodología de referencia se encuentra el Aprendizaje Significativo, cuyo primer requisito para que se produzca es la potencialidad significativa del material de aprendizaje, la cual está compuesta por dos dimensiones que Ausubel distingue como:

• Significatividad lógica, se refiere a la coherencia en la estructura interna del material, secuencia lógica en los procesos y consecuencia en las relaciones entre sus elementos componentes.

• Significatividad psicológica, se refiere a que sus contenidos sean comprensibles desde la estructura cognitiva que posee el sujeto que aprende.

• El segundo requisito es la disposición positiva del individuo respecto del aprendizaje, se refiere al componente motivacional, emocional, actitudinal que está presente en todo aprendizaje, ya que este no puede darse si el alumno no quiere. Este es un componente en donde el maestro sólo puede influir a través de la motivación.

    Constituyen principios bases de la Didáctica de las Ciencias:

1. El Principio de la correlación entre lo cualitativo y lo cuantitativo: Es necesario que durante el proceso de aprendizaje se entrene a los estudiantes en la realización de valoraciones cualitativas de los enunciados y resultados cuantitativos de los ejercicios y problemas así como de cualquier otro planteamiento que lo permita.

2. El Principio de la importancia y utilidad socio-cultural del contenido: En el proceso de enseñanza aprendizaje es necesario dirigir las acciones de tal modo que se le revele al educando lo útil que resulta el contenido que se le va a enseñar, convenciéndolo (sin imposiciones) de la necesidad que existe de que él lo aprenda.

II.     Condiciones previas necesarias para la aplicación de la metodología

Para el docente

1.     Dominio del diagnóstico del estudiante

    Sin lugar a dudas, el diagnóstico integral debe constituir para los docentes un punto de partida para lograr una mejor concepción y ejecución de la actividad a proyectar en el proceso formativo. Son elementos imprescindibles conocer: qué sabe el estudiante, cómo lo hace, cómo aprende, cómo piensa, cómo se comporta en la formación de las acciones valorativas, cuáles son sus cualidades, etc.

2.     Dominio del contenido

    Este es un aspecto capital para el eficiente desempeño del docente, por lo que es importante que la autopreparación sea sistemática y profunda, utilizando primero la bibliografía básica y complementaria orientada al estudiante y luego ampliando la misma con otras bibliografías disponibles.

3.     Resolución de los problemas que propondrá

    Para poder garantizar un desarrollo de habilidades exitoso es imprescindible que el docente tenga resuelto de antemano los problemas que propondrá en el encuentro o como trabajo independiente, Lo que permitirá graduar el sistema de ejercicio de acuerdo al orden de complejidad de manera ascendente.

4.     Estructuración lógica del material a impartir

    La potencialidad significativa o lógica del material es la primera condición para que se produzca el aprendizaje del estudiante, esta estructuración tiene que cumplir con dos aspectos:

1. El material presentado al estudiante debe estar organizado, para que se de una construcción de conocimientos.

2. Y que pueda conectar el nuevo conocimiento con los que ya posee para que lo comprenda.

Para el alumno

1.     Estar motivado para aprender

    Al estudiante hay que explicarle que la Física cumple una doble función: por un lado sus conocimientos son utilizados directamente en alguna asignatura de la especialidad (ejemplo en la Biomecánica), y por el otro, su función está en desarrollar el pensamiento lógico, el trabajo con algoritmos y métodos de solución.

2.     Dominio de los conocimientos previos necesarios

    Existen determinados conocimientos antecedentes que son necesarios fijar en el estudiante, con el objetivo de que logren aplicar con éxito cada uno de los pasos de la metodología, los cuales se enumeran a continuación:

• El comportamiento de la velocidad en cada uno de los movimientos mecánicos estudiados.

• De cada fuerza estudiada saber: quién la ejerce, como se representa y como calcularla.

• La descomposición de un vector en sus componentes y cómo calcular el valor de las componentes.

• Dominar de cada tipo de movimiento mecánico estudiado, la ley del movimiento que lo explica.

• Dominar de las ecuaciones que relacionan a la mecánica de la traslación y la rotación.

III.     Pasos de la metodología para la solución de problemas por la vía dinámica.

Primer Paso: Elegir el sistema físico a trabajar

• El más sencillo de los sistemas físicos para elegir es siempre el cuerpo al cual se le estudia el movimiento.

Segundo Paso: Representar el sistema físico como un punto material

• Se representa el sistema como un círculo y se representan las fuerzas desde el centro geométrico del mismo.

Tercer Paso: Representar las fuerzas que actúan sobre el sistema físico

    Para esto debes determinar:

• ¿Cuáles son los cuerpos que interactúan con el sistema físico?

• ¿Qué fuerza aporta cada uno de estos cuerpos?

• Representar las fuerzas encontradas.

• En el caso de la rotación representar solo aquellas fuerzas que le provocan torque o momento de fuerza al sistema.

Cuarto Paso: Trazar un sistema de coordenadas y orientar los ejes

• Hacer coincidir el origen de coordenadas con el centro del sistema físico.

• Situar uno de los ejes de coordenadas en la dirección en que se mueve el cuerpo (paralelo a la superficie) y orientarlo en el sentido del movimiento, el otro eje se traza perpendicular al primero y se orienta para donde se desee.

Quinto Paso: Descomponer las fuerzas que no estén sobre los ejes de coordenadas trazados:

• Utilizar el método de descomposición de un vector en coordenadas rectangulares para obtener las componentes y su valor en cada eje.

Sexto Paso: Escribir la Ley de Newton que se cumple en cada eje:

    Para esto debes determinar:

• ¿Qué le ocurre a la velocidad del cuerpo en cada eje?

• ¿Qué tipo de movimiento corresponde al cuerpo en cada eje?

• Tomando como base el tipo de movimiento determinado, escribir la ley de Newton que se cumple para cada eje.

• En la rotación se escribe la ley de Newton que se cumple de acuerdo al tipo de movimiento del sistema.

Séptimo Paso: Resolver la sumatoria de fuerza y proyectar la ecuación:

• Se suman vectorialmente todas las fuerzas que están en cada eje.

• Para proyectar la ecuación, cada fuerza se escribe sin vectores, con signo positivo si su sentido coincide con el del eje y con signo negativo si su sentido es contrario al eje.

• En la rotación, los torques que actúan en sentido de la rotación son positivos y los que actúan contrario son negativos.

• A la aceleración se le pone signo positivo si tiene un MRUA o MCUA y signo negativo si tiene un MRUR o MCUR.

Octavo Paso: Operar con las ecuaciones de ambos ejes hasta encontrar la incógnita

Noveno Paso: Sustituir, calcular y obtener el resultado

Décimo Paso: Analizar y comprobar la solución

    A continuación se ilustra con un ejemplo cómo proceder en la solución de un problema derivado de la práctica deportiva.

    Ejemplo resuelto: Se conoce que durante la carrera de impulso el centro de masa de un saltador de longitud, de 78 kg de masa, experimentó una aceleración horizontal aproximadamente constante e igual a 0,88 m/s2. Conociendo que el coeficiente de fricción entre el saltador y la pista es de 0.15, determine la fuerza de tracción horizontal que estuvo actuando sobre él. Desprecie la fricción con el aire.

    Solución: De la interpretación y análisis realizado al problema podemos resumir los datos y la incógnita. En este caso como no influye la forma del sistema que se mueve, el cuerpo del atleta lo podemos representar como un cuadrado.

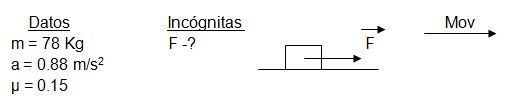
    Aplicando el método dinámico de solución de problemas.

1º paso: Nuestro sistema físico será el saltador.

2º paso: Al representar el cuerpo como un punto material, nos queda:

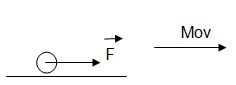
3º paso: Representar las fuerzas que actúan sobre el sistema físico.

• ¿Cuáles son los cuerpos que interactúan con el sistema físico?

La tierra, la superficie y el agente externo.

• ¿Qué fuerza aporta cada uno de ellos?

La tierra, la fuerza de gravedad (Fg).

La superficie, la normal (N) y la fuerza de fricción (fr) ya que es rugosa

El agente externo, la fuerza (F).

• Ahora podemos representarlas sobre el sistema físico.

4º paso: Trazar el sistema de coordenadas rectangulares.

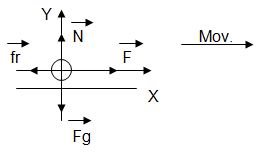
5º paso: Como todas las fuerzas están sobre los ejes de coordenadas, no hay que descomponerlas.

6º paso: Escribir la ley de Newton que se cumple en cada eje.

    Para ello responderemos las preguntas propuestas para este paso, relacionadas con cada eje.

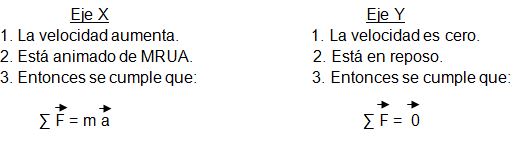
7º paso: Resolver la sumatoria y proyectar la ecuación.

8º paso: Como tenemos que calcular la fuerza de tracción, y se encuentra en la ecuación del eje X, nos queda:

F = ma + fr

    En los datos no disponemos del valor de la fuerza de fricción, hay que calcularla:

fr = μ N, la fuerza normal (N) se calcula a partir de la ecuación del eje y. Luego:

N – Fg = 0, despejando:

N = Fg, y como Fg = m g, queda:

N = m g, que al sustituirla en fr, resulta:

fr = μ m g, sustituyendo en la ecuación de la fuerza se obtiene:

F = m a + μ m g

F= m (a + μ g)

9º paso: Sustituir y calcular:

F = 78 kg (0.88 m/s2 + 0.15 * 9.81 m/s2)

F = 183,417 N

10º paso: Es sencillo verificar la solución, al estar en presencia de una ecuación lineal, solo hay que comprobar la igualdad de ambos miembros.

    Tenemos que la fuerza de tracción horizontal es la componente horizontal de la fuerza con que el atleta acciona sobre la pista, y que por reacción (según la tercera ley de Newton) la pista le ejerce a él acelerándolo.

    Finalmente, esta metodología se ejemplificó para el estudio mecánico de una carrera, pero la misma es útil para estudiar los movimientos en el deporte, por complejos que parezcan, ya que todos están sujetos a las leyes del movimiento mecánico.

Conclusiones

1. El Enfoque Histórico Cultural, el Aprendizaje Significativo y la Didáctica de la Física contemporánea, permiten sustentar la metodología elaborada para favorecer el proceso de enseñanza aprendizaje de la Biomecánica, a través de la resolución de problemas de Mecánica, en la carrera de Licenciatura en Cultura Física.

2. El estudio diagnóstico realizado, permitió determinar que aún es insuficiente el aprendizaje de la Biomecánica y de sus métodos de resolución de problemas.

3. La metodología elaborada constituye una vía eficaz para la orientación del proceso de solución de problemas facilitando su explicación y comprensión por parte de los estudiantes.

Referencias bibliográficas

• Álvarez de Zayas, Carlos (1990) Fundamentos teóricos de la dirección del Proceso Docente Educativo en la Educación Superior Cubana. La Habana.

• Álvarez de Zayas, C. (1985) Fundamentos de la metodología de la enseñanza de la Física. La Habana, Material mimeografiado, ISP Enrique José Varona. 85 p.

• Ausubel, D. P y col. (1991) Psicología Educativa. México, Editorial Trillas. 352 p.

• Donskoi, D y V. Zatsiorski. (1988) Biomecánica de los ejercicios físicos. La Habana, Editorial Pueblo y Educación. 312 p.

• Gómez Zoque, Alexis (2004) Introducción a la Didáctica de las Ciencias. Holguín, ISP “José de la Luz y Caballero”. 176 p.

• Nápoles Valdés, Juan E. (2002) Aventuras, venturas y desventuras de la resolución de problemas en la escuela. Argentina, Universidad de la Cuenca de la Plata, Corrientes.

• Palacio Peña, Joaquín (2001) Hacia una mayor efectividad en la enseñanza de problemas matemáticos. Curso Preevento, Congreso Internacional Pedagogía, La Habana.

• Polaino de los Santos, Lázara (2003) ¿Qué es la Biomecánica? En Universalización de la Cultura Física. Materiales bibliográficos, La Habana, ISCF Manuel Fajardo.

• Rizo C. y Campistrous L. (1997) Estrategias de resolución de problemas en la escuela. La Habana, Ponencia Evento Internacional Pedagogía '97.

• Sifredo Barrios, C. y Cabrera, C. (1987) Orientaciones metodológicas para la solución de problemas de Física. 10. Grado. La Habana, Editorial Pueblo y Educación. 52 p.

• Talizina, N. F. (1998) Psicología de la Enseñanza. Moscú, Editorial Progreso.

• Vigotsky, L. S (1987). Historia del desarrollo de las funciones psíquicas superiores. La Habana, Editorial Científico Técnica.

Otros artículos sobre Biomecánica

	Búsqueda personalizada
EFDeportes.com, Revista Digital · Año 18 · N° 182 | Buenos Aires, Julio de 2013   © 1997-2013 Derechos reservados