Algoritmos para la medición de centros de  gravedad corporal en plataformas convencionales
	*Médico y Cirujano. Licenciado en Matemáticas Magíster en Ciencias de la Actividad física y el Deporte **Licenciado en Educación Física. Especialista en Entrenamiento Deportivo Magíster. Dr. en Ciencias del Deporte ***Médico especialista en Medicina Deportiva Docentes vinculados al Politécnico Colombiano Jaime Isaza Cadavid (Colombia)	Juan Cancio Arcila Arango jcarcilaa@elpoli.edu.co Donaldo Cardona Nieto dcardona@elpoli.edu.co Juan Carlos Giraldo García juangiraldo@elpoli.edu.co
	Resumen           Existen varios métodos validados para la medición de los centros de gravedad en diferentes posiciones corporales. Nos basamos en los procedimientos más aceptados y utilizados en la actualidad, principalmente las propuestas de Reynolds, Lovett y Basler. La medición de centros de gravedad puede servir para el manejo, la promoción y la educación para la salud de los sistemas corporales en poblaciones específicas, no solo de deportistas competitivos, sino también de deportistas recreativos, personal laboral, personas con enfermedades de base (hipertensión arterial, diabetes mellitus, dislipidemias, alteraciones del tejido conjuntivo, etc.) o en proceso de rehabilitación posterior a traumas, discapacitados y otros. El análisis de los centros de gravedad adquiere gran importancia en la interpretación de las posturas corporales humanas tanto estáticas como dinámicas, así como en la discusión de los movimientos del cuerpo considerado como una partícula donde se supone que se concentra todo el peso del sistema. Estudiando la trayectoria de dicha partícula representativa donde se ubica el centro de gravedad, es posible realizar análisis cinemáticos lineales de los movimientos rectilíneos y curvilíneos y, análisis cinemáticos angulares de los movimientos rotatorios. En este trabajo se ofrecen herramientas alternativas para establecer un hilo conductor entre la valoración del centro de gravedad y los posibles efectos benéficos del entrenamiento objetivo en todas las poblaciones, situación que abre las puertas para la exploración de muchos parámetros determinantes en la integridad corporal en búsqueda de un equilibrio bio-sico-social.           Palabras clave: Medición de centros de gravedad. Postura corporal.   Abstract           Several methods for measuring validated the centers of gravity in different body positions. We rely on the procedures accepted and used today, mainly proposals Reynolds, Lovett, Basler and segmental methods. The centers of gravity measurement can serve for the management, promotion and health education of the body systems in specific populations, not only competitive athletes, recreational athletes but also, workforce, people with underlying diseases (hypertension pressure, diabetes mellitus, dyslipidemia, abnormal tissue, etc..) or in the process of post-trauma rehabilitation, disabled and others. Analyzing the center of gravity becomes very important in the interpretation of the human body postures both static and dynamic, as well as in the discussion of the movements of the body considered as a particle where it is assumed that all the weight is concentrated in the system. Studying the trajectory of the representative particle which houses the center of gravity, kinematic analysis is possible linear rectilinear and curvilinear movements and angular kinematic analysis of rotational movements. In this paper we provide alternative tools to establish a common thread between the valuation of the center of gravity and the possible beneficial effects of the workout target all populations, a situation that opens the door for exploration of many key parameters in seeking bodily integrity balance of bio-psycho-social.           Keywords: Measuring gravity centers. Posture.
	EFDeportes.com, Revista Digital. Buenos Aires - Año 18 - Nº 181 - Junio de 2013. http://www.efdeportes.com/

1 / 1

Introducción

    El cuerpo humano es un sistema biológico dinámico que ocupa un lugar en el espacio, está compuesto por estructuras denominadas segmentos corporales, cada una de las cuales tiene un peso que corresponde a la fuerza de atracción que la tierra ejerce sobre él. Por ello es necesario localizarlo, situarlo de manera eficiente y rápida, utilizando planos y ejes (Hernández Corvo, 1990).

    De manera muy simple, ignorando el hecho de que la distribución de la masa de la tierra no es perfectamente esférica, Serway (1998) define el peso como la fuerza ejercida por la tierra sobre un objeto, con dirección hacia el centro de la tierra. Según McGinnis (1999) “El centro de gravedad es un concepto útil para el análisis del movimiento humano, ya que es el punto en el que se puede considerar que se concentra toda la masa o el peso del cuerpo. Por lo tanto la fuerza de la gravedad actúa hacia abajo a través de este punto. Si una fuerza externa neta actúa sobre el cuerpo, la aceleración causada por ella es la eceleración del centro de gravedad. Si no actúa una fuerza externa sobre el objeto, el centro de gravedad no se acelera”.

    Integrando ambos conceptos, en este trabajo se asume que el peso es una magnitud vectorial cuyo punto de aplicación es el “baricentro” o “centro de gravedad” del segmento, aquel punto imaginario donde podemos considerar que se acumula la resultante de los pesos de sus infinitos elementos másicos. En forma análoga, pero discretizando el modelo general, podemos considerar que el centro de gravedad del cuerpo humano total, es aquel punto imaginario donde se aplica la resultante de acumular el efecto de los pesos de un número finito de segmentos corporales.

    Estos elementos son de la mayor importancia, dado que en la bipedestación anatómica convencional, la desviación de la línea de acción del peso corporal (fuerza externa ejercida por la tierra sobre el cuerpo) puede ser indicio de un inbalance muscular, de un vicio postural o de alguna patología o lesión secundaria a traumatismo. El uso de una plataforma de fuerza de dos planos para medir el centro de presión en ambos pies por separado (Murray et al., 1973) ha demostrado ser de valor en la evaluación de las asimetrías en el control postural en el envejecimiento y en la enfermedad. El método más común ha sido cuantificar el desequilibrio en la carga de peso entre los pies (Myklebust et al., 2009). Si se hace un diagnóstico temprano, se pueden implementar medidas para su corrección, aunque lo ideal sería la aplicación de estrategías tendientes a promover la salud del aparato locomotor y a prevenir sus anormalidades.

Desarrollo

    Según acuerdo de la Nómina Anatómica Parisina ratificado en París en el Congreso Internacional de Anatomía de 1955 y, posteriormente sostenido hasta la actualidad por la Comisión Internacional de Nomenclatura (Guillen y Linares, 2002), se asume una posición de referencia para el cuerpo humano denominada “Posición Anatómica” con las siguientes características: cuerpo en bipedestación, pies separados orientados en ligera rotación externa formando un ángulo de 45°, los miembros superiores descargados con los codos en extensión, con las palmas dirigidas hacia delante, los dedos extendidos y los pulgares orientados hacia afuera. Hernández Corvo (1990) prefiere dinamizar esta posición clásica dándole al antebrazo dos expresiones de movimiento: supinación en el antebrazo derecho (la palma queda dirigida hacia delante con el pulgar orientado hacia afuera) y pronación en el antebrazo izquierdo (la palma queda orientada hacia atrás con el pulgar orientado hacia dentro). Moore et al. (2007) en su Anatomía con orientación clínica, plantean que todas las descripciones anatómicas deben expresarse en relación con una posición anatómica de referencia, para asegurar que las descripciones no sean ambiguas: el cuerpo de pie, la cabeza, mirada (ojos) y dedos dirigidos anteriormente, brazos adyacentes a los lados con las palmas de las manos mirando hacia delante, los miembros inferiores juntos con los pies paralelos y los dedos dirigidos anteriormente. Izquierdo (2008) reconoce que la posición clásica anatómica, utilizada por anatomistas, biomecánicos y fisiólogos, es un punto de referencia importante para iniciar el análisis del movimiento, pero, al igual que los biomecánicos en la actualidad, prefiere la denominada “Posición Fundamental” por la mayor similitud de esta con las posiciones de inicio de diferentes actividades deportivas y cotidianas. A diferencia de la posición anatómica, en la posición fundamental los miembros superiores con los codos extendidos, están pegados al cuerpo con las manos en posición neutra (palmas dirigidas hacia adentro con los pulgares orientados hacia delante). Los pies mantienen una separación con ligera rotación externa, contrariando la posición fundamental descrita por Luttgen y Wells (1982) en la que los pies asumen una orientación paralela hacia delante, posición incómoda para la musculatura tónica postural de los miembros inferiores.

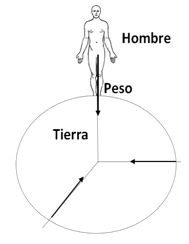
Figura N°1. Fuerza de atracción gravitacional

    Para el cuerpo humano sobre la tierra, su vector peso se dirige hacia el centro de la tierra obedeciendo a la segunda ley de Newton: Fuerza = masa x aceleración (F = m . a). Como en este caso, la fuerza es el peso del cuerpo y la aceleración es la gravitacional, la expresión para el peso corporal es Peso = masa x gravedad (P = m . g).

    Claramente la fórmula expresa que “El peso es la relación variable y adaptativa entre masa y gravedad” (Hernández Corvo, 1992). Un cambio en la cantidad de materia (masa) es responsable de un cambio en el peso cuando se comparan en dos momentos diferentes. Así, por ejemplo, una persona previamente pesada en reposo, pesará menos después de realizar un ejercicio durante una hora, pues la eliminación de líquidos y calorías, supone una disminución de la masa. Aquí la gravedad ha permanecido constante al considerar que la persona permanece en el mismo sitio geográgico. Si instantáneamente, se pudiese medir el peso de una persona en dos lugares a diferentes latitudes, la masa sería la misma, pero la gravedad sería diferente, variación que estaría generando un valor de peso corporal diferente. En los polos la tierra es más achatada, razón por la cual está más cercana al centro de la tierra ( radio polar ≈ 6.356,9 km)y la aceleración gravitacional es mayor. En cambio, en la línea ecuatorial hay una mayor distancia al centro de la tierra ( radio ecuatorial ≈ 6.378,4 km), razón por la cual la aceleración gravitacional es menor (figura Nº1). En general, el valor promedio es g = 9,8 m/s², pero hay una variación aproximada de ± 0,05% de ese valor. Así, una persona pesa más en los polos donde g = 9,8309 m/s² , que en el perímetro ecuatorial donde g = 9,7789 m/s². Para el cálculo exacto de la aceleración gravitacional, Hochmuth (1973) tiene en cuenta la latitud geográfica φ de acuerdo con la fórmula

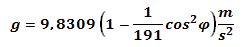
    Las denominaciones de centro de masa, centro de gravedad y baricentro, pueden ser utilizadas como análogas. Hablando de equilibrio y estabilidad, Davidovits (2001) expone que la tierra ejerce una fuerza de atracción de la masa de un objeto, de hecho, cada pequeño elemento de la masa del objeto es atraído por la tierra. La suma de estas fuerzas es el peso total del cuerpo, el cual se puede considerar como una fuerza que actúa a través de un único punto llamado centro de masa o centro de gravedad.

    Actualmente hay varias perspectivas relativas a la ubicación del centro de gravedad del cuerpo humano para hombres y mujeres en posición anatómica:

1. Por delante de la segunda vértebra sacra en hombres y, 3 cm más abajo en mujeres (Viladot, 2001).

2. En un punto situado del 56% al 57% de la altura corporal medida desde el suelo en hombres y, 55% en mujeres (Guillén y Linares, 2002).

    Las diferencias por género se deben entre otras a las siguientes razones: las mujeres poseen una cintura pélvica más amplia y una pelvis más ancha, sus extremidades son más cortas y, su índice de masa magra/masa adiposa es menor; los hombres poseen una cintura escapular más amplia, sus extremidades son más largas y su índice de masa magra/masa adiposa es mayor.

    Esta ubicación del centro de gravedad varía constantemente con la ejecución de diferentes actividades cotidianas y de gestos deportivos. Durante la marcha por ejemplo, en el apoyo unilateral en la locomoción, el cuerpo desciende al propulsarse sobre la pierna extendida, generando un ascenso del centro de gravedad de aproximadamente 5 cm.

    Adicionalmente, cuando el sistema corporal se desplaza en el aire y despreciamos las fuerzas disipativas como resistencia del aire, de tal forma que sobre él actúe solamente la fuerza conservativa gravitacional, su centro de gravedad describe una trayectoria parabólica que combina un movimiento rectilíneo uniforme horizontal y un movimiento rectilíneo uniformemente variado vertical, donde la aceleración es –g cuando asciende y es +g cuando desciende. Tal es el caso de de ejecuciones atléticas como los saltos y los lanzamientos, o de diversos gestos gimnásticos. Pudiera decirse por ejemplo que, los saltadores más eficáces son aquellos que mejor manejan su centro de gravedad corporal y, los gimnastas más armoniosos ajustan sus ejes de giro cruzando por su centro de gravedad, de tal forma que este sea el centro de giro del sistema. Se debe aclarar que el centro de gravedad es instantáneo dependiendo de la posición relativa durante la ejecución de un gesto, esto es, no está permanentemente dentro del cuerpo, sino que puede ser extracorpóreo como en el caso determinante de la altura máxima en un salto alto o en un salto con pértiga, situaciones en las que el baricentro debe quedar por debajo del cuerpo para vencer el listón. Otra situación fundamental sobre el centro de gravedad cuando actúa como centro de rotación del sistema, radica en el hecho de los torques o momentos generados por las diferentes fuerzas que actúan sobre él. Aquellas fuerzas, cuyas líneas de acción pasan por el centro de gravedad, no producen un efecto rotatorio sobre el sistema y, por tanto sus torques son nulos, así, tales fuerzas afectarían solamente los movimientos de traslación corporal. En cambio, producen torque aquellas fuerzas cuyas líneas de acción no lo cruzan, pudiendo modificar los movimientos de traslación y rotación.

    Para la medición de centros de gravedad de los cuerpos se requieren algunas herramientas matemáticas que expresan las condiciones de equilibrio estático: la sumatoria de las fuerzas que actúan sobre el sistema es nula 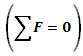, lo que se denomina equilibrio traslacional (Jou et al., 1994) y, la sumatoria de los torques (o momentos lineales) respecto a

algún punto del sistema también es nula 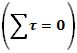, lo que se denomina equilibrio rotacional (Jou et al., 1994). El torque de una fuerza con respecto a un punto o a un eje de

 rotación () se define como el producto de dicha fuerza por la distancia perpendicular al punto o eje de rotación, el signo se asume positivo en sentido antihorario (contrario al movimiento de las agujas del reloj) y, negativo en sentido horario.

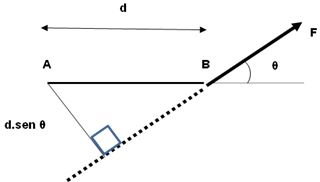
Figura N°2. Efecto rotacional de una fuerza

    En la figura Nº2, la fuerza F se aplica en el punto B formando un ángulo 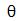con la prolongación del segmento rectilíneo AB, así que el torque de la fuerza F respecto al punto de rotación A es: 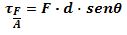el cual tiene signo positivo.Cuando lafuerza es perpendicular al segmento rectilíneo que representa la distancia, ocurre 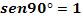razón por la 

cual el torque es simplemente t = F . d.

    En términos técnicos del análisis vectorial, si el vector de desplazamiento 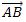se define desde el eje de rotación que pasa por el punto A hasta el punto B de aplicación de la fuerza 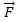, el producto vectorial de la fuerza y ​​el vector desplazamiento es un nuevo vector que se conoce como el momento de fuerza M, de modo que .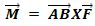 

La distancia perpendicular 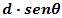desde el eje de rotación a la línea de acción de la fuerza se conoce como el brazo de momento de la fuerza. Para la aplicación elemental que se necesita en esta revisión, el módulo del producto vectorial o producto cruz (Enoka, 2002) es igual al producto de los módulos de los vectores multiplicado por el seno del ángulo que forman entre sí.  Así que 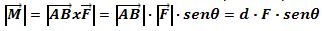que es el mismo torque de la fuerza F con respecto al centro de rotación A. Tal como lo expresa

Robertson et al. (2004), algunos textos de física e ingeniería hacen una distinción entre los términos momento de fuerza y torque, asocian el torque ya sea con pares de fuerzas o movimientos de "torsión" en las que es difícil identificar un único vector fuerza y su punto de aplicación. Dentro de la comunidad biomecánica, los términos se utilizan indistintamente.

    Gutiérrez (1999) expone que en la actualidad hay varios métodos de medición del centro de gravedad que permanecen vigentes:

1.     Reynolds y Lovett (1909) diseñaron una plataforma rectangular de madera (simetría geométrica) con densidad homogénea y peso WP aplicado en el centro de gravedad o “baricentro” que, bajo tales circunstancias, coincide con el centro geométrico o “centroide” ubicado en el punto P equidistante de dos pivotes. La plataforma está apoyada en sus dos extremos por dos pivotes, uno de rozamiento considerado nulo (punto A) y otro apoyado sobre una balanza (punto B) que registra la fuerza WB que ejerce sobre dicho extremo. (fig. Nº3).

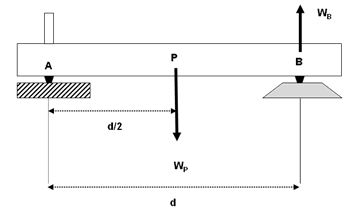
Figura N°3. Vista lateral de la plataforma uniplanar rectangular

    Nótese que ambas fuerzas son perpendiculares a los segmentos rectilíneos que representan las distancias. Aplicando la condición de equilibrio estático para este sistema considerando los torques respecto al punto A tenemos:

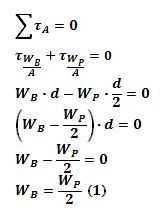
    Ahora, acostando el sujeto en posición de decúbito dorsal sobre la plataforma, de tal forma que sus pies hagan contacto con el tablón vertical ubicado en el punto A:

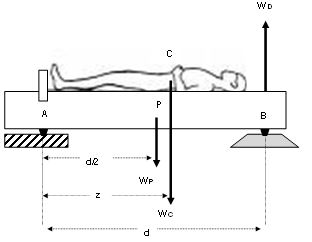
Figura N°4. Hombre acostado sobre la plataforma uniplanar rectangular

    Nótese que las tres fuerzas son perpendiculares a los segmentos rectilíneos que representan las distancias. Aplicando la condición de equilibrio estático para este sistema considerando los torques respecto al punto A tenemos:

   

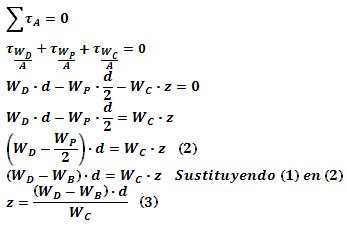
    La ecuación (3) expresa el valor real de la cota del centro de gravedad corporal, es decir, la tercera coordenada en el sistema espacial.

    El peso del hombre Wc está aplicado en un punto C ubicado a una distancia Z (ecuación (3)) del punto A. Claramente, los parámetros del lado derecho de la ecuación (3) son conocidos: WB y WD son las lecturas de la balanza (sin hombre y con hombre, respectivamente), Wc es el peso del hombre medido previamente en otra balanza y, d es la distancia conocida entre los dos pivotes, medida con una cinta métrica.Este valor real z debe compararse con la cota teórica de la fórmula de Guillén y Linares (2002):

    De manera simplificada, si se ajusta a cero la lectura de la balanza sin la persona, WB será cero en la ecuació (3) resultando: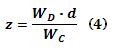

    Donde WD es la lectura de la balanza con el hombre sobre la plataforma, Wc es el peso del hombre medido previamente en otra balanza y d es la distancia conocida entre lod dos pivotes, medida con una cinta métrica.

2.     Plataforma para la valoración de huellas plantares

    Se utiliza también otra plataforma biplanar de madera de dos cuerpos para la valoración de huellas plantares que permiten evaluar el tipo de pie y la ubicación del centro de gravedad de la base de sustentación en posición de bipedestación. Un primer cuerpo tiene forma rectangular y sirve de soporte para hacer el apoyo plantar sobre el segundo cuerpo. Este último, es en forma de triángulo rectángulo isóceles, donde uno de sus dos lados iguales se coloca paralelo y próximo a uno de los lados menores del rectángulo. Bajo el vértice del triángulo que corresponde al ángulo recto hay un pivote de rozamiento denominado nulo y, los otros dos vértices se apoyan sobre dos balanzas que registran las fuerzas que realizan sobre los dos extremos.

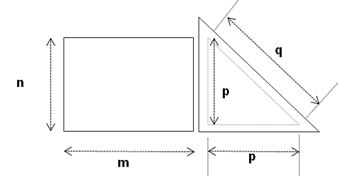
Figura N°5. Vista superior de la plataforma biplanar

 

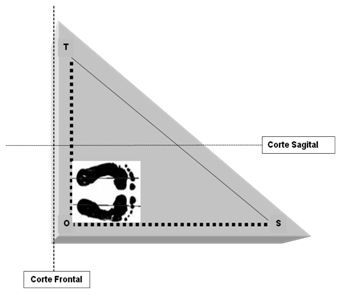
Figura N°6. Huellas plantares en la superficie triangular de la plataforma biplanar

    Sobre el triángulo de madera se colocan unas cintas métricas paralelas a los lados iguales (OT y OS), de tal forma que el punto de intersección O sea precísamente el apoyo sobre el pivote de rozamiento nulo. La distancia “p” se mide desde este punto O hasta los puntos T y S donde están ubicados los pivotes de balanza.

    El valor de “q” se puede calcular aplicando el teorema de Pitágoras al triángulo rectángulo .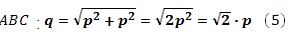 

    El valor “p” es conocido ya que es el que se conviene en la construcción de la plataforma, al igual que los valores “m” y “n”.

    Se consideran dos planos de corte: uno frontal, que hace una división antero-posterior y ubica el centro de gravedad en un paraplano sagital y, otro sagital que hace una división derecha-izquierda y ubica el centro de gravedad en un paraplano frontal.

    En el cuerpo rectangular se coloca una silla, la persona se sienta en ella e introduce sus pies en una cubeta de madera que tiene su superficie bañada en alcohol industrial, así las plantas quedan impregnadas de alcohol. Posteriormente, en unasegunda cubeta de madera, que se hace coincidir con el vértice rectangular del triángulo y sobre la cual se colocan simétricamente y adosadas dos hojas de papel fax con el lado más liso hacia arriba, los pies deben apoyar partiendo de talones hacia las puntas y luego la persona debe pararse. Resultan unas sombras y unas huellas claras (en tono rosado), estas últimas son las que se utilizan para la medición.

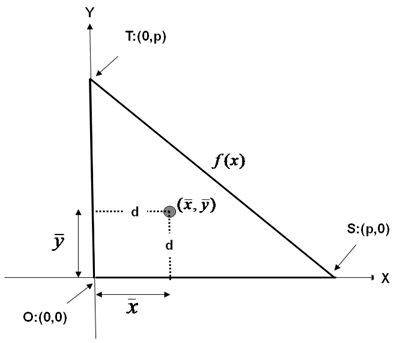
Figura N° 7. Centroide de la superficie triangular

    La pendiente del segmento rectilíneo TS puede ser calculada por la fórmula 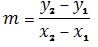(Neuhauser, 2004) de modo . 

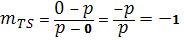    Ahora utilizamos la ecuación punto-pendiente para determinar la ecuación de la recta 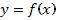que contiene al segmento TS:

   

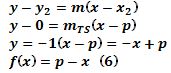
    Nótese además que el área del triángulo es: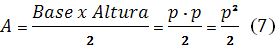

    Del Cálculo Integral (Stewart, 2006), las coordenadas del centroide estarán dadas por las expresiones:

   

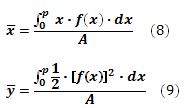
    Reemplazamos (6) y (7) en (8):

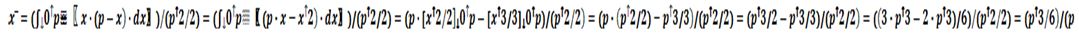
    Así, hemos calculado la abscisa del centroide de la plataforma, el cual depende del valor “p” del lado con que deseemos construirla.

    Ahora, reemplazando (6) y (7) en (9):

   

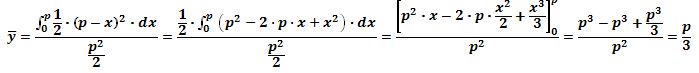
    Así, hemos calculado la ordenada del centroide de la plataforma triangular, el cual depende del valor “p” del lado con que deseemos construirla.

    En definitiva, las coordenadas del centroide de la plataforma son: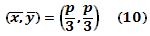

    Nótese que por el principio de simetría, de acuerdo a la construcción de triángulo isóceles en el sistema elegido, era de esperarse que coincidiera el valor de ambas coordenadas.

    La distancia “d” desde el centroide a cada uno de los lados iguales es claramente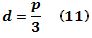

    Si consideramos un eje de giro que coincida con el lado OS, la fuerza Ws que ejerce la balanza en S contra el vértice correspondiente no produce torque, así que la condición de equilibrio para los torques de las otras fuerzas será:

   

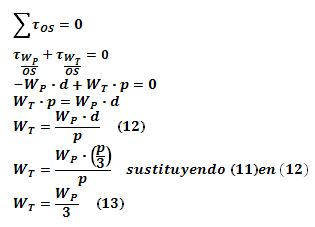
    Si consideramos un eje de giro que coincida con el lado OT, la fuerza WT que ejerce la balanza en T contra el vértice correspondiente no produce torque, así que la condición de equilibrio para los torques de las otras fuerzas será: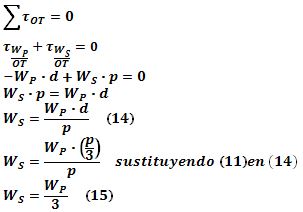

   

    Comparando (13) y (15) observamos que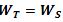

    Ahora, parando el sujeto en bipedestación sobre la plataforma, su centro de gravedadestará ubicado en un punto a una distancia “x” del lado OT y, a una distancia “y” del lado OS (figura Nº8). Estos son los parámetros que debemos determinar, ya que el peso WG se aplica en el punto (x, y).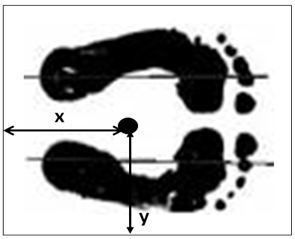

Figura Nº8. Centro de gravedad de la base de sustentación

    Si consideramos un eje de giro que coincida con el lado OT, la fuerza WT que ejerce la balanza en T contra el vértice correspondiente no produce torque, así que la condición de equilibrio para los torques de las otras fuerzas será: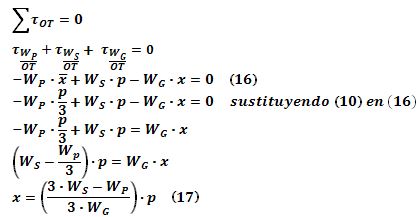

   

    La ecuación (17) expresa el valor real de la abscisa del centro de gravedad corporal.

    Si consideramos un eje de giro que coincida con el lado OS, la fuerza WS que ejerce la balanza en S contra el vértice correspondiente no produce torque, así que la condición de equilibrio para los torques de las otras fuerzas será: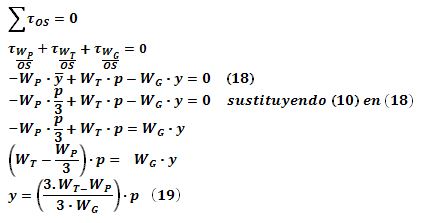

   

    La ecuación (19) expresa el valor real de la ordenada del centro de gravedad corporal.

    Así, el centro de gravedad del cuerpo estará ubicado para la posición de bipedestación en un punto ubicado a una distancia “x” del lado OT y a una distancia “y” del lado OS. Así, las coordenadas del centro de gravedad de la base de sustentación son:

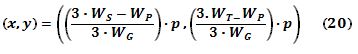
    Este resultado debe compararse con el centro de gravedad esperado de acuerdo al análisis geométrico de las huellas en la Base de Sustentación (BS). Según Izquierdo (2008) en su libro Biomecánica y bases neuromusculares de la actividad física y el deporte, la BS es el área encerrada al unir los puntos de apoyo más externos. En el cuerpo humano la BS queda delimitada por los márgenes externos del apoyo de los dos pies y todo lo que queda entre ellos. La relación entre la BS y la proyección vertical del centro de gravedad indica si el cuerpo está equilibrado o desequilibrado. Una vez que el centro de gravedad se sale de la BS, el cuerpo se desequilibra y, si no se hace nada por evitarlo, se caerá. Como nuestros cuerpos son articulados, podemos modificar la forma y el tamaño de la BS cambiando la posición de los pies. La medición del centro de gravedad esperado en la BS se realiza de la siguiente manera: se traza una línea paralela al borde inferior del rectángulo de papel pasando por el punto más posterior de la huella de retropie, luego se trazan dos perpendiculares a esta pasando por los puntos más externos de los bordes laterales de ambos pies, excluyendo el quinto artejo y, finalmente se completa el rectángulo con una línea paralela a la primera, pasando por el punto más anterior de la huella del antepie en los dedos (ver figura Nº9). El punto de intersección de las dos diagonales de este rectángulo, da las coordenadas del centro de gravedad esperado o deseado del apoyo en bipedestación 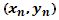. Así, se pueden hacer comparaciones que evidencien inbalances corporales y, determinar el grado de los mismos.

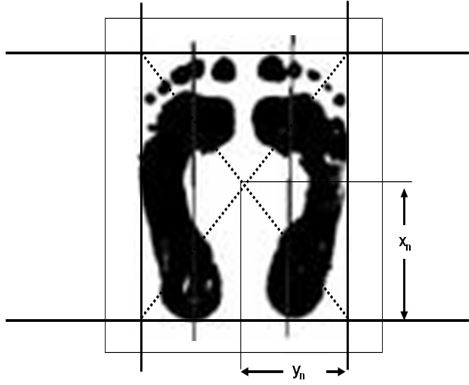
Figura Nº9. Centro de gravedad esperado de la BS

    En definitiva, según las ecuaciones (3) y (20) las coordenadas espaciales reales del centro de gravedad son:

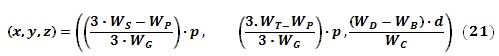
    que se comparan con las coordenadas teóricas 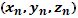para determinar asimetrías y disbalances corporales, mediante el análisis del desplazamiento de cada una de las coordenadas:

   

    De manera simplificada, si se ajustan a cero las lecturas de las balanzas sin la persona, WP y WB serán cero en la ecuación (21) resultando: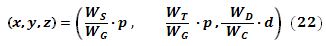

    Donde WS, WT y WD son las lecturas de las balanzas con el hombre sobre las plataformas,WC (o WG) es el peso del hombre medido previamente en otra balanza, d es la distancia conocida entre los dos pivotes en la plataforma rectangular y p el valor de uno de los lados iguales de la plataforma triangular.

3.     La plataforma equilátera de Basler utiliza un procedimiento similar al anterior para el cálculo del centro de gravedad del cuerpo humano en dos dimensiones. Se trata de una plataforma de madera, triangular y equilátera (sus tres lados iguales) que, al igual que la anterior presenta simetría geométrica y densidad homogénea, razón por la cual su centro de gravedad (baricentro) coincide con su centro geométrico (centroide). Según Zatsiorski (1990), se trata de un método experimental en el que los tres vértices de la plataforma se apoyan sobre tres pivotes, uno de rozamiento considerado nulo (en el punto A) y, los otros dos están apoyados sobre dos balanzas (en los puntos B y C), que registran las fuerzas WB y WC que ejercen sobre los vértices correspondientes (figura Nº10).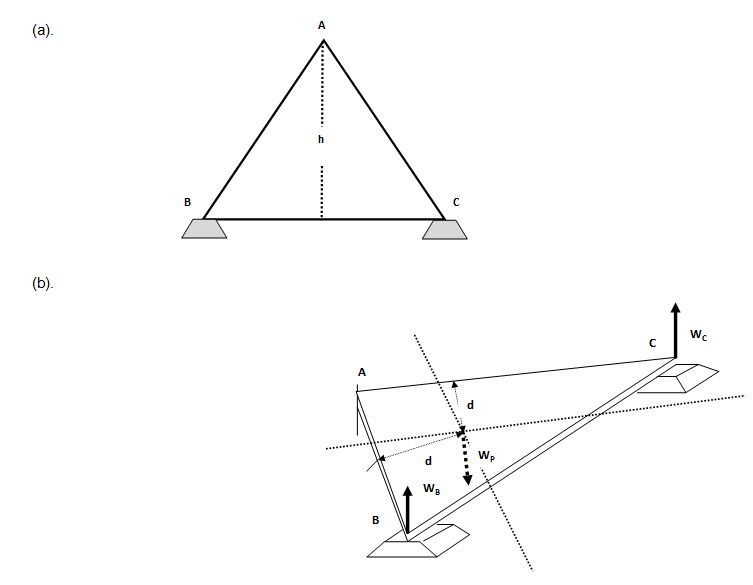

Figura Nº10. Plataforma equilátera de Basler

    El centro de gravedad de la plataforma está ubicado en algún punto sobre el segmento rectilíneo que representa la altura h y en la intersección de dos líneas rectas: una paralela al lado AB y otra paralela al lado AC. Así, el peso de la plataforma (WP) se aplica en un punto ubicado a una distancia perpendicular “d” del lado AB y, a una distancia perpendicular “d” del lado AC.

    Si consideramos un eje de giro que coincida con el lado AB, la fuerza WB que ejerce la balanza en B contra el vértice correspondiente no produce torque, así que la condición de equilibrio para los torques de las otras fuerzas será: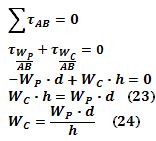

   

    Si consideramos un eje de giro que coincida con el lado AC, la fuerza WA que ejerce la balanza en A contra el vértice correspondiente no produce torque, así que la condición de equilibrio para los torques de las otras fuerzas será: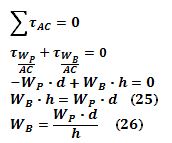

   

    Observamos que (24) = (26), por lo que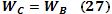

    En las ecuaciones (24) y (26), los valores 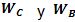son conocidos por las lecturas de las balanzas correspondientes, pero los valores de h y d son por ahora desconocidos. Para encontrar el valor de h podemos utilizar elementos geométricos y trigonométricos elementales (figura Nº11), a partir de la situación de un triángulo equilátero en el cual, todos sus lados son iguales (a = b = c) y todos sus ángulos internos son iguales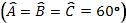

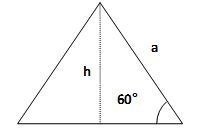
Figura Nº11. Relaciones en el triángulo equilátero

   

Además, podemos calcular el área de dicho triángulo:

   

    La distancia d puede ser calculada a partir de las coordenadas del centroide 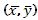de la plataforma considerada como una placa triangular equilátera de densidad homogénea. Si ubicamos el triángulo en un sistema biaxial de coordenadas cartesianas de tal manera que uno de sus lados coincida con el semieje positivo X y uno de sus vértices coincida con el origen del sistema 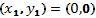, entonces sus otros dos vértices tendrán coordenadas 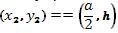el superior y 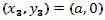el derecho, tal como se observa en la

figura Nº12.

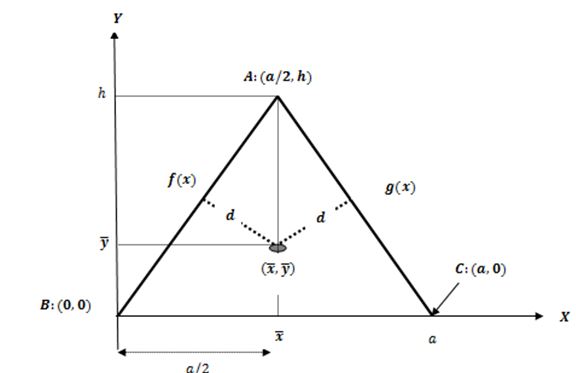
Figura Nº12. Análisis de la plataforma equilátera en un sistema cartesiano

   

    Así, hemos calculado la abscisa del centroide de la plataforma, el cual depende del valor "a" del lado con que deseemos construirla.

    Ahora, reemplazando (30), (31) y (32) en (34)

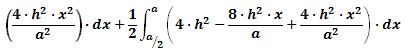
    Al reemplazar (28) en (37) se obtiene:

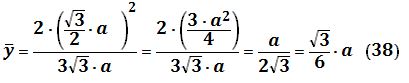
    Así, hemos calculado la ordenada del centroide de la plataforma, el cual depende del valor "a" del lado con que deseemos construirla.

    En definitiva, las coordenadas del centroide de la plataforma son:

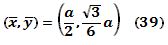
    Nótese que por el principio de simetría, de acuerdo a la construcción triangular equilátera en el sistema elegido, pudo determinarse inicialmente la abscisa del centroide sin necesidad de los cálculos efectuados. Pero el ejercicio resulta interesante y necesario para calculos en el caso general de plataformas triangulares no equiláteras.

    Reemplazando (28), (36) y (38) en (40):

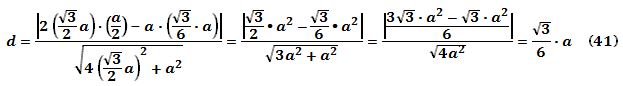
    que por simetría es el mismo valor de la ordenada del centroide. Además, también es claro por simetría que la abscisa del centroide es .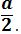

    Ahora, acostando el sujeto en cualquier posición sobre la plataforma, su centro degravedad estará ubicado en un punto a una distancia perpendicular"xG" del lado AB y, a una distancia perpendicular"yG" del lado AC (figura Nº12). Estos son los parámetros que hay que determinar.

    Si consideramos un eje de giro que coincida con el lado AB, la fuerza WR que ejerce la balanza en B contra el vértice correspondiente no produce torque, así que la condición de equilibrio para los torques de las otras fuerzas será: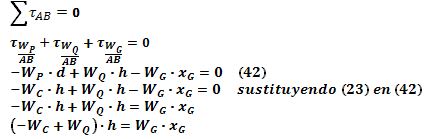

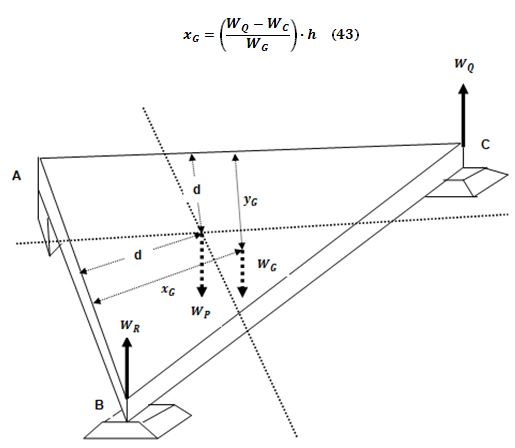
Figura Nº13. Torques para hombre acostado sobre la plataforma equilátera de Basler (No se representa gráficamente el hombre por comodidad en el análisis vectorial)

    Si consideramos un eje de giro que coincida con el lado AC, la fuerza WQ que ejerce la balanza en C contra el vértice correspondiente no produce torque, así que la condición de equilibrio para los torques de las otras fuerzas será: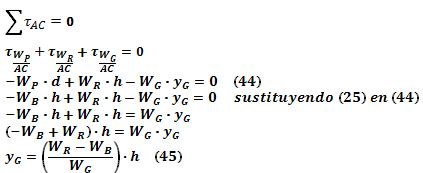

   

    Así, el centro de gravedad del cuerpo en el gesto elegido, estará ubicado en el punto de intersección de dos líneas que distan"xG" e "yG" de los lados AB y AC respectivamente, dadas por las ecuaciones (40) y (42). Las coordenadas del centro de gravedad de la persona en la plataforma equilátera de Basler serán: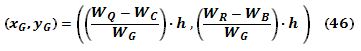

Conclusión

    Los métodos experimentales y las herramientas del cálculo se complementan magistralmente para resolver el problema de la determinación de los centros de masa del cuerpo humano en posiciones relativas de reposo y movimiento. El análisis comparativo de las coordenadas espaciales experimentales y teóricas, permite conocer los desplazamientos del baricentro en situaciones tanto fisiológicas como patológicas. En consecuencia, posibilita junto con otros estudios posturográficos y pedigráficos, no solo un abordaje fisioterapéutico más preciso y eficaz, sino también, una intervención oportuna para promover la higiene postural y prevenir lesiones osteomusculares.

Bibliografía

• Ahonem, Jarmo y Lahtinem, Tina. Kinesiología y anatomía aplicada a la actividad física. 2ª ed. Barcelona: Paidotribo. 2001.

• Davidots, Paul. Physics in biology and medicine. Complementary Science Series. 2ª ed. Orlando (Florida): Harcourt/Academic Press. 2001.

• Enoka, Roger. Neuromechanics of human movement. 3ª ed. Champaign: Human Kinetics. 2002.

• Guillén del Castillo, M. y Linares Girela, D. Bases biológicas y fisiológicas del movimiento humano. Madrid: Médica Panamericana, S.A. 2002.

• Gutiérrez Dávila, Marcos. Biomecánica deportiva. 1ª reimpresión. Madrid: Síntesis. 1999.

• Hernández Corvo, Roberto. Enciclopedia general del ejercicio. Tomo III: El sistema locomotor. Barcelona: Paidotribo, S.A. 1990.

• Hernández Corvo, Roberto. Morfología funcional deportiva. Función de apoyo. Medellín: Piloto Ltda. 1992.

• Hochmuth, Gerhard. Biomecánica de los movimientos deportivos. 1ª ed. Instituto Nacional de Educación Física. Ciencia y Deporte. Madrid: Doncel.1973.

• Izquierdo, Mikel. Biomecánica y bases neuromusculares de la actividad física y el deporte. Madrid: Médica Panamericana S.A. 2008.

• Jou, David; Lebot, Josep y García, Carlos. Física para ciencias de la vida. 1ª ed. Madrid: McGraw-Hill Interamericana, S.A. 1994.

• Luttgens, Kathryn y Wells, Katharine. Kinesiología. Bases científicas del movimiento humano. 7ª ed. Saunders College Publishing. Madrid: Pila Teleña. 1982.

• Mc Ginnis, Peter M. Biomechanics of sport and exercise. 2ª ed. Champaign, IL.: Human Kinetics. 1999.

• Moore, Keith L.; Dalley, Arthur F. y Agur, Anne M. Anatomía con orientación clínica. 5ª ed. Buenos Aires: Médica Panamericana, S. A. 2007.

• Murray, M. P.; Peterson, R. M. Weigth distribution and weight-shifting activity during normal standing posture. Phys Ther 1973; 53:741-8.

• Myklebust, J. B.; Lovett, E. G.; Myklebust, B. M.; Reynolds, N.; Milkowski, L.; Prieto, T. E. Two-dimensional coherence for measurement of asymmetry in postural steadiness. Gait & Posture. 29 (2009) 1-5.

• Neuhauser, Claudia. Calculus for biology and medicine. 2a ed. New Jersey: Pearson – Prentice hall. 2004.

• Robertson, D. Gordon; Caldwell, Graham; Hamill, Joseph; Kamen Gary and Whittlesey. Research methods in biomechanics. Champaign, IL.: Human Kinetics: 2004.

• Serway, Raymond. Física. Tomo I. 4a ed. México: McGraw Hill Interamericana. 1998.

• Stewart, James. Cálculo, conceptos y contextos. 3ª ed. México: Thomson: 2006.

• Viladot Voegeli, Antonio. Lecciones básicas de biomecánica del aparato locomotor. : Barcelona: Springer. 2001.

• Zatsiorski, Vladimir. Biomecánica de los ejercicios físicos. Manual. La Habana: Pueblo y Educación. 1990.

Otros artículos sobre Biomecánica

	Búsqueda personalizada
EFDeportes.com, Revista Digital · Año 18 · N° 181 | Buenos Aires, Junio de 2013   © 1997-2013 Derechos reservados