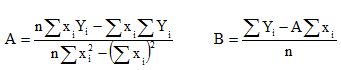|
|||
|---|---|---|---|
|
|
Ajuste da curva monoexponencial da cinética do VO 2: um estudo com Excel®
Ajuste de la curva monoexponencial de la cinética de VO2: un estudio con Excel®
|
|
|
|
*Mestre em Ciência da Motricidade Humana pela UCB, RJ **Professora do Departamento de Matemática da Universidade Regional do Noroeste do Estado do Rio Grande do Sul (UNIJUÍ) Mestre em Matemática pela UNIJUÍ, RS (Brasil) |
Nelson Kautzner Marques Junior* Tânia Michel Pereira** |
|
|
|
Resumo O objetivo do artigo de revisão foi ensinar o ajuste da curva monoexponencial da cinética do VO2 através do Excel®. Unitermos: Cinética do VO2. Ajuste de curva. Matemática. Exercício. Exponencial. Excel ®.
Abstract The objective of the review article was to teach the monoexponential curve fit of the VO2 kinetics with Excel®. Keywords: VO2 kinetics. Curve fit. Mathematics. Exercise. Exponential. Excel®.
|
|||
|
|
EFDeportes.com, Revista Digital. Buenos Aires - Año 18 - Nº 180 - Mayo de 2013. http://www.efdeportes.com/ |
|
|
1 / 1
Introdução
Em 1913, através de Krogh e Lindhard, aconteceu um dos primeiros estudos que observou o aumento da cinética do VO2 (consumo de oxigênio) em resposta ao exercício moderado de 12 minutos1. Após a pesquisa de Hill e Lupton2 publicado em 1923, sobre a cinética do VO2 durante e no fim do exercício, vários cientistas passaram investigar esse fenômeno com frequência3,4. Em 1954, Astrand e Ryhming evidenciaram que a cinética do VO2 durante o esforço físico tinha um comportamento linear5. Muitas discussões aconteceram sobre a linearidade e não linearidade do comportamento da cinética do VO26,7. Mas a partir de 1990, Whipp e Ward concluíram através de uma revisão de literatura que a cinética do VO2 se apresentava não linear durante e após o exercício8. Essa informação foi corroborada em pesquisa de campo9.
A resposta da cinética do VO2 durante o exercício aumenta de maneira exponencial conforme prossegue a atividade física, podendo atingir um platô quando o indivíduo atinge o estado estável no trabalho predominantemente aeróbio10. A literatura da fisiologia do exercício divide a curva da cinética do VO2 em três fases11. A fase I ou fase cardiodinâmica acontece nos primeiros segundos (geralmente entre 10 e 25 segundo) do aumento da resposta do VO2 ao exercício, esta resposta está relacionada principalmente com o aumento da frequência cardíaca, com um maior fluxo sanguíneo nos músculos e da maior resposta respiratória12,13. A fase I da cinética do VO2 costuma ser ajustada através de uma equação monoexponencial14. A fase II ou componente rápido inicia logo após o término da fase I, ela pode durar a partir de alguns segundos até uns poucos minutos (geralmente entre 25 a 80 segundo)15. Nessa fase o VO2 continua com um aumento exponencial, não permitindo ao indivíduo um estado estável (steady state). A fase II a cinética do VO2 costuma ser ajustada por uma equação biexponencial16. Caso o exercício continue, acontece a fase III ou componente lento do VO2 (geralmente possui 80 segundos ou mais), que pode acontecer o estado estável se o esforço físico for moderado17. A fase III a cinética do VO2 costuma ser ajustada por uma equação biexponencial ou triexponencial, estando relacionada com a intensidade do exercício18.
A cinética do VO2 após o exercício atualmente é denominada de consumo excessivo de oxigênio pós-exercício, sendo também chamada através da abreviação do inglês de EPOC (excesso postexercise oxygen consumption). Krogh e Lindhard foram um dos primeiros a estudar a cinética do VO2 após o esforço físico, isso ocorreu em 192019. Enquanto que Hill, Long e Lupton explicaram em 1924 sobre o metabolismo energético durante e após o exercício, eles informaram que no término da atividade física acontece um débito de oxigênio20, hoje denominado EPOC. Esse trabalho pioneiro de Hill et alii20, serviu de base para Margaria, Edwards e Dill estabelecerem em 1933 que durante o débito de oxigênio ocorre duas fases, o débito aláctico e o débito láctico21.
Atualmente o EPOC é dividido em rápido (geralmente entre 10 a 180 segundos) e lento (180 segundos até muitas horas), também sendo identificado o EPOC ultralento (mais de 24 horas)22. Após a interrupção da atividade física o VO2 diminui de maneira exponencial tendo valores superiores ao antes do esforço físico, geralmente o EPOC rápido é ajustado por uma curva monoexponencial e o EPOC lento por uma curva biexponencial23. O objetivo do EPOC é restaurar os processos metabólicos pós-exercício, por exemplo, no EPOC rápido ocorre uma restauração dos fosfagênios e um reabastecimento dos estoques de oxihemoglobina (hemoglobina combinada ao O2)24, no EPOC lento acontece significativa remoção do lactato e diminuição da ventilação pulmonar25 e no EPOC ultralento, parece que ele se manifesta em exercícios intensos com alto demanda de ação muscular excêntrica, merecendo mais investigação sobre a sua atuação26.
A figura 1 ilustra as explicações anteriores sobre a cinética do VO2 durante e após o exercício12.
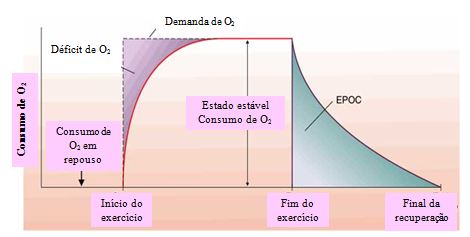
Figura 1. Crescimento exponencial do VO2 durante o exercício
e decaimento exponencial do VO2 após o esforço físico12.
Após a escolha do melhor modelo exponencial para a cinética do VO2 durante o exercício e após a atividade – detalhes em Marques Junior27, o pesquisador precisa realizar um ajuste exponencial da curva do VO2. Segundo Guimarães28, “ajustar uma curva a um conjunto de pontos obtidos num experimento é encontrar a função matemática que mais se aproxima do comportamento daquele conjunto de dados obtidos no laboratório” (p. 49). Um dos cálculos mais utilizados para o ajuste de curva foi elaborado por Carl Gauss em 1809, artigo publicado no Werke, a equação foi denominada de condições que minimizam a soma dos quadrados dos resíduos, posteriormente essa equação foi chamada por Adrien-Marie Legendre de método dos mínimos quadrados29. O objetivo do método dos mínimos quadrados é estabelecer matematicamente uma diferença mínima entre os dados de um experimento30,31. O ajuste da curva através dos mínimos quadrados não necessita de equipamentos sofisticados, pode ser facilmente resolvido com o uso de uma calculadora32, mas para agilizar os pesquisadores, esse artigo vai ensinar como utilizar o Excel® nessa equação.
O objetivo do artigo de revisão foi ensinar o ajuste da curva monoexponencial da cinética do VO2 através do Excel®.
Ajuste da curva da cinética do VO2 com Excel®
O artigo elaborado por Marques Junior ensinou como determinar o melhor modelo exponencial para a curva do VO2 durante e após o exercício27. Esse artigo é a continuação desse trabalho porque vai orientar o pesquisador como ajustar a curva da cinética do VO2.
Utilizando o mesmo exemplo de Marques Junior27, dois sujeitos foram selecionados para um experimento, ficaram em pé por 5 minutos com o analisador de gases portátil Cosmed K4 b2 para coletar o VO2. Após esse procedimento, os dois sujeitos correram numa velocidade máxima por um período de 1 minuto e 20 segundos (80 segundos) e o Cosmed K4 b2 coletou o VO2 do esforço físico em cada 5 segundos. A figura 2 mostra como os dados se comportaram durante a coleta através de uma curva do VO2 não ajustada (Obs.: Esses dados não são reais).
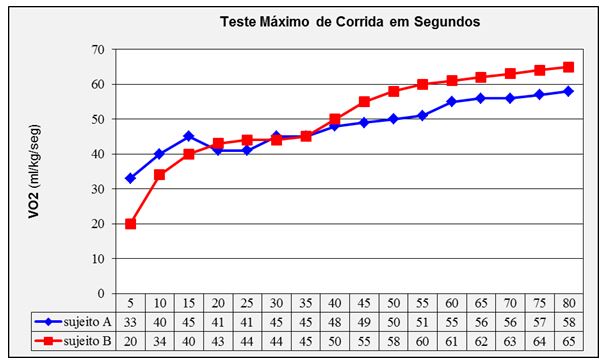
Figura 2. VO2 do teste de corrida
Após esse procedimento foram realizados vários cálculos e foi estabelecido que o melhor ajuste da curva do VO2 do teste de corrida foi através de um modelo monoexponencial – veja os cálculos em Marques Junior27. Para o pesquisador realizar o ajuste da curva monoexponencial da cinética do VO2 basta praticar os seguintes procedimentos:
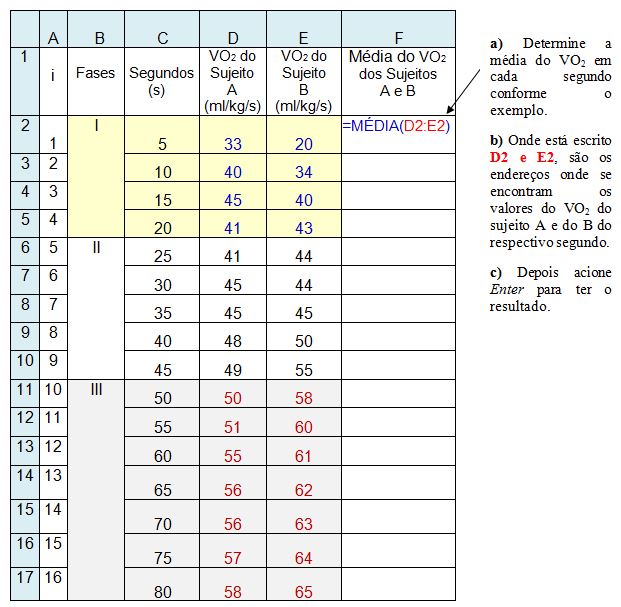
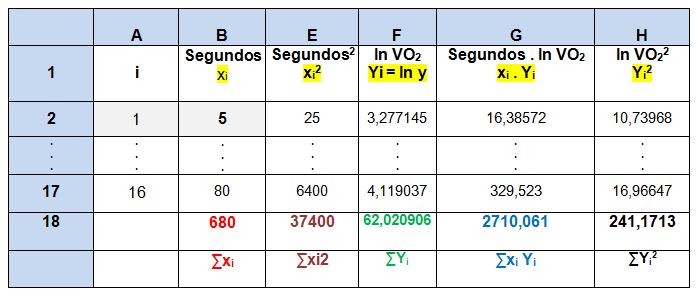
1. Organize no Excel® o VO2 de cada sujeito em uma tabela e coloque o identificador das linhas, o i (O i varia de 1 a 16 nessa coleta de dados) que consequentemente, você vai determinar o n (n é a quantidade de dados colhidos em cada segundo, sendo 16) da amostra.
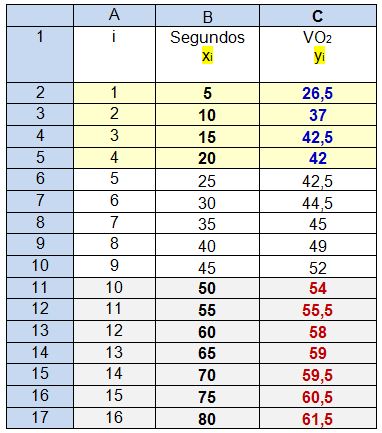
2. Organize no Excel® outra tabela com a média do VO2 em cada segundo. Segundo você vai se referir como xi e VO2 como yi.
3. Baseado em Pereira33, vamos realizar todos os procedimentos para efetuar o método dos mínimos quadrados:
a) Para fazer o ajuste da exponencial da forma
y=a.ebx (1)
basta fazer as transformação necessárias para linearização na equação desta.
b) Considerando que y é um valor positivo isto implica que o valor de a, da equação (1) é positivo. Desta forma é possível aplicar o logaritmo natural (In) em ambos os membros e obtém-se
ln (y) = ln (aebx) (2)
c) Aplique a propriedade do produto e é encontrado ln (y) = ln a + ln ebx .
d) Aplique a propriedade da potência e tem-se ln (y) = ln a + bx, visto que ln e=1. e) Faça Y= ln (y), A= b e B= ln (a) e fazendo as substituições em ln (y) = ln a + ln bx tem-se Y= Ax + B. Note que os parâmetros a e Y= Ax + B da função monoexponencial y = a . ebx após linearizada, podem ser obtidos a partir dos valores de A e B utilizando o método dos mínimos quadrados para a equação da reta.
f) Calcule os valores de A e B a partir das seguintes equações abaixo utilizando a planilha eletrônica Excel l®. ou outra similar.
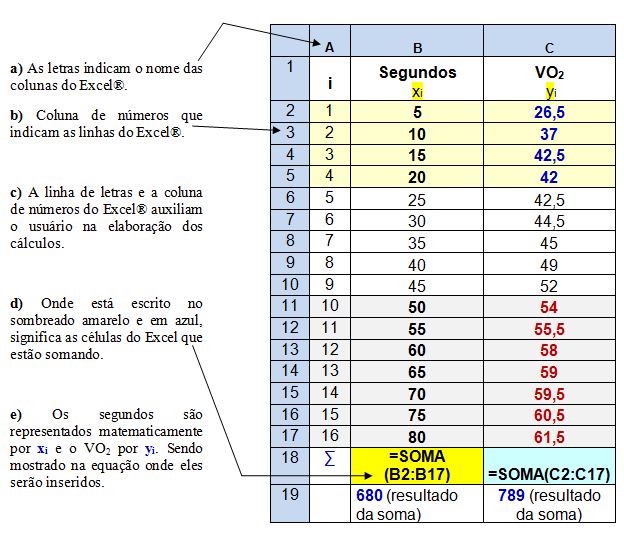
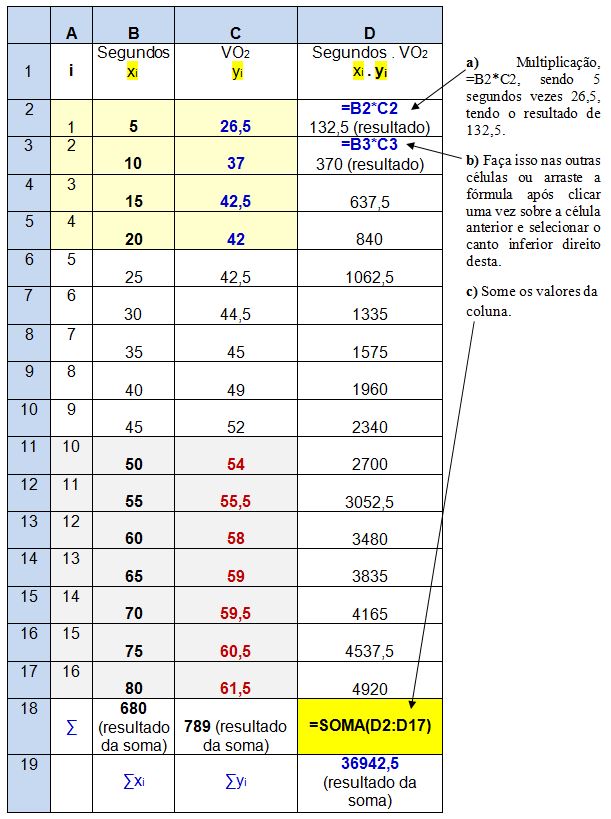
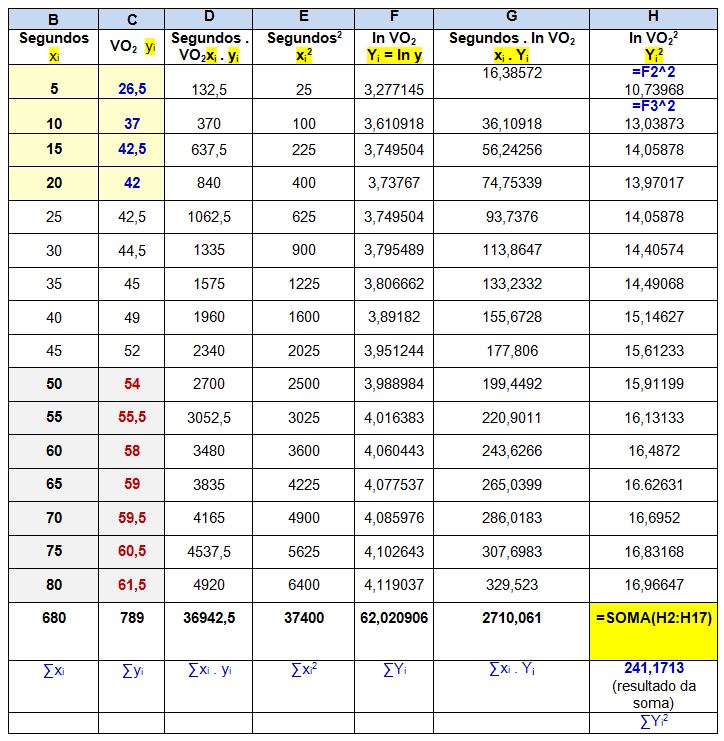
4. Multiplique os segundos (xi) pelo VO2 (yi) e depois some os resultados.
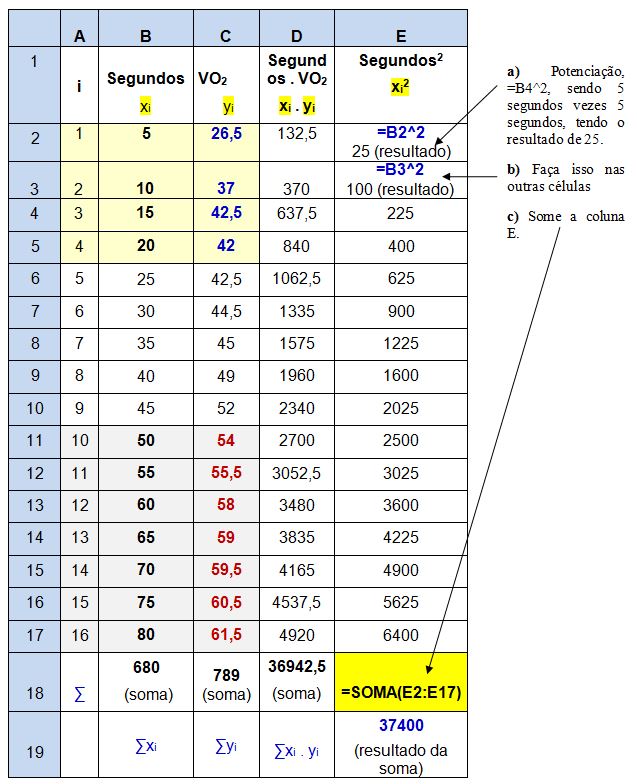
5. Os segundos que matematicamente é xi, devem ser elevados ao quadrado, sendo representados por xi2.
Exemplo do cálculo realizado: 5 segundos 52 = 5 x 5 = 25
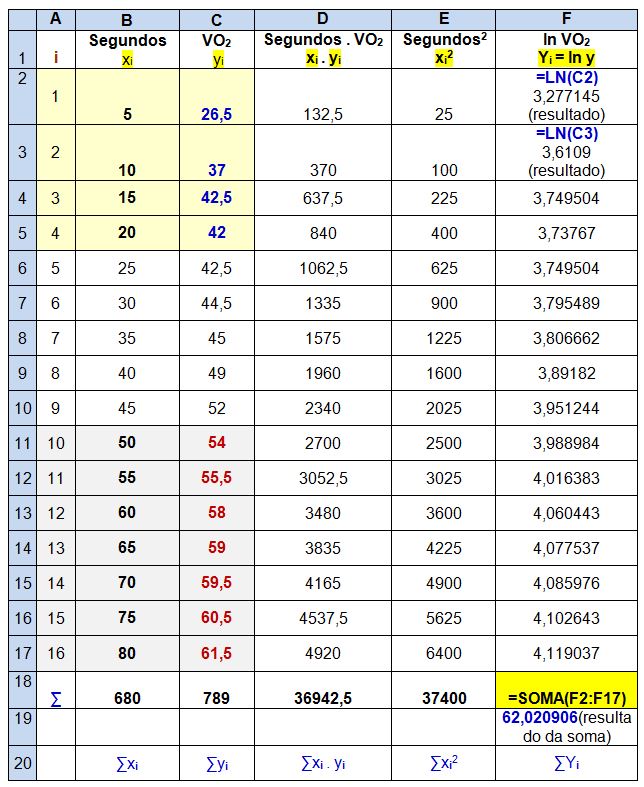
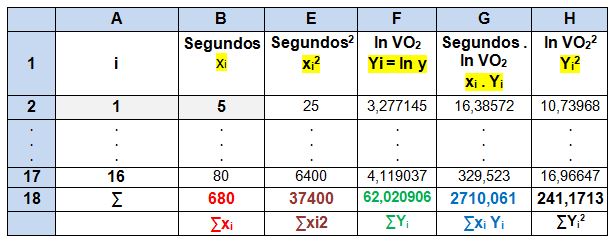
6. Determine o logaritmo natural do VO2, sendo representado matematicamente por Y = In y. Depois some toda a coluna, sendo ∑Yi.
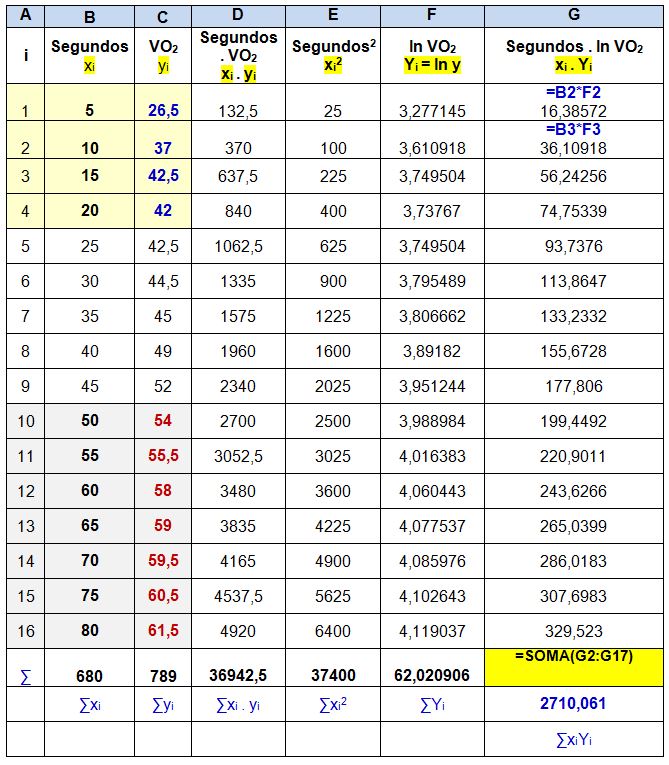
7. Continuando a seguir os ensinamentos de Pereira33, multiplique os segundos (xi) pelo logaritmo natural do VO2 (Yi). Depois some toda a coluna, sendo ∑xi . Yi.
8. Eleve o resultado do logaritmo natural do VO2 ao quadrado (Yi2), depois some os valores da coluna (∑Yi2).
9. Depois de calcular todas as variáveis da equação A e B, resolva de acordo como Pereira33 determina.
Lembre que n=16 (número de dados).
a) Obtenha o valor de A da fórmula a seguir por calculadora.
b) Fazendo o cálculo na célula B28 do Excel®, basta ver onde estão os resultados e digitar as letras e os números que correspondem aquela célula com o símbolo da conta (* é multiplicação, / é divisão, ^ é potência, - é menos). O cálculo de A fica o seguinte:
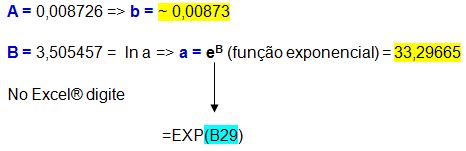
c) Obtenha o valor de B por calculadora com a fórmula a seguir.
d) Obtendo o valor de B no Excel® , na célula B29.
Lembrando que Y= ln (y), A= b e B= ln (a)
e)
f) A equação da reta dos mínimos quadrados da função monoexponencial possui a seguinte estrutura:
g) Então estruture a equação monoexponencial do VO2 em função do tempo s Substituindo y por VO2 e x por t:
10) Calcule o VO2 utilizando a função monoexponencial atribuindo valores para t utilizados durante a observação e coloque estes valores na coluna I.
Cálculo com calculadora.a)
Substitua t por 5s na função
Consulte a tabela de função exponencial crescente para substituir o número 0,04365. Esse detalhe você pode ver em Marques Junior27.
Resultado do VO2 ajustado no período de 5 segundos: 34,78 ml/kg/seg
11. Compare os resultados do VO2 calculados com os observados colocando-os na coluna I, conforme mostrado no quadro a seguir.
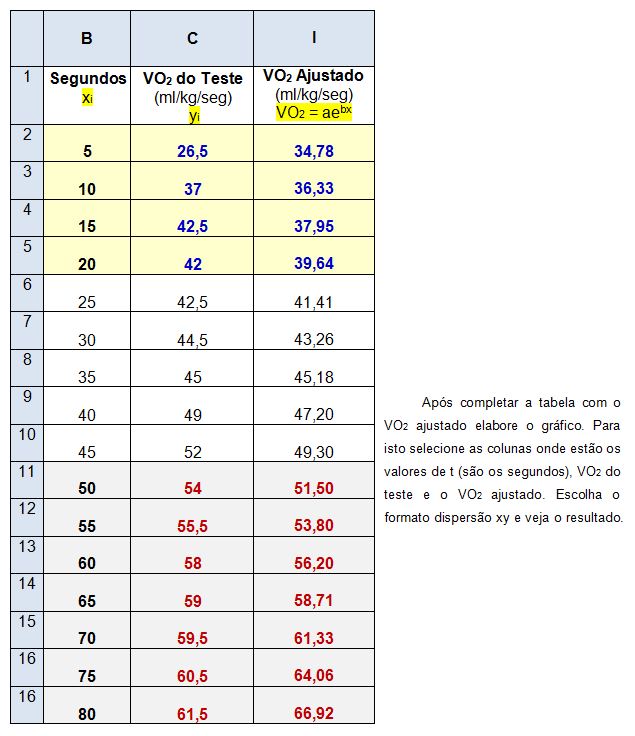
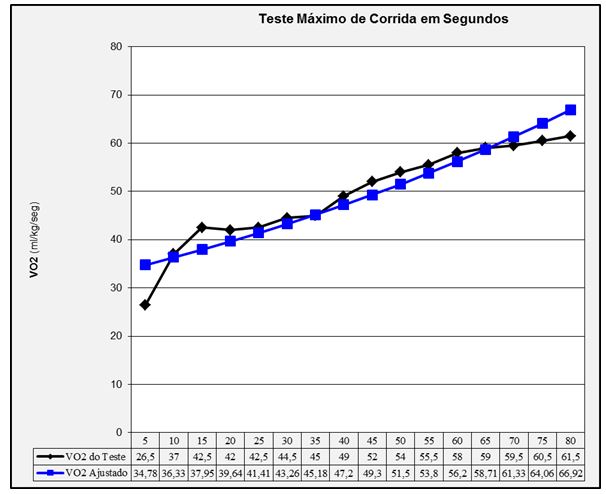
Figura 2. Resultado do VO2 do teste e do VO2 ajustado da curva monoexponencial
12. Calcule o coeficiente de determinação (R2) baseado em Pereira33. Segundo Guidorizzi34, quanto mais próximo de 1 estiver o R2, melhor será a ajuste da reta dos mínimos quadrados aos pontos da tabela. Use os valores calculados anteriormente.
Fazendo por calculadora.a)

b) No Excel® a fórmula da equação fica da seguinte maneira:

Através desses cálculos você pode ajustar a curva monoexponencial do VO2, podendo fazer o mesmo no EPOC.
Conclusão
O ajuste da curva monoexponencial da cinética do VO2 com o Excel® é uma tarefa demorada e minuciosa, mas quando elaborado no programa torna-se fácil e prazeroso efetuar esses cálculos e possibilitado a compreensão do processo todo.
Referências
-
Krogh A, Lindhard J (1913). The regulation of respiration and circulation during the initial stages of muscular work. J Physiol 47(1-2):112-36.
-
Hill A, Lupton H (1923). Muscular exercise, lactic acid, and the supply and utilization of oxygen. Q J Med 16(-):135-71.
-
Barstow T, Molé P (1991). Linear and non-linear characteristics of oxygen uptake kinetics during heavy exercise. J Appl Physiol 71(6):2099-2106.
-
Damasceno M et alii (2011). Relação entre a cinética do consumo de oxigênio e a estratégia de corrida em uma prova de 10 km. Rev Bras Med Esporte 17(5):354-7.
-
Astrand PO, Ryhming I (1954). A nomogram for calculation of aerobic capacity (physical fitness) from pulse rate during submaximal work. J Appl Physiol 7(2):218-21.
-
Hughson R (1990). Exploring cardiorespiratory control mechanisms through gas Exchange dynamics Med Sci Sports Exerc 22(1):72-9.
-
Legge B, Banister E (1986). The Astrand-Ryhming nomogram revisited. J Appl Physiol 61(3):1203-9.
-
Whipp B, Ward S (1990). Physiological determinants of pulmonar gas exchange kinetics during exercise. Med Sci Sports Exerc 22(1):62-71.
-
Zoladz et alii (2007). Non-linear relationship between oxygen uptake and power output in the Astrand nomogram – old data revisited. J Physiol Pharmacol 58(2):265-73.
-
McArdle W, Katch F, Katch V (2011). Fisiologia do exercício: nutrição, energia e desempenho humano. 7ª ed. Rio de Janeiro: Guanabara. p. 169-82.
-
Reis J et alii (2012). Effects of aerobic fitness on oxygen uptake kinetics in heavy intensity. Eur J Appl Physiol 112(5):1689-97.
-
Wilmore J, Costill D (2001). Fisiologia do esporte e do exercício. 2ª ed. São Paulo: Manole, 2001. p. 134-6.
-
Bell C et alii (2001). A comparison of modeling techniques used to characterize oxygen uptake kinetics during the on-transient of exercise. Exper Physiol 80(-):667-76.
-
Gurd B et alii (2009). Prior heavy exercise elevates pyruvate dehydrogenase activity and muscle oxygenation and speeds O2 uptake kinetics during moderate exercise in older adults. Am J Physiol – regul, integr compar physiol 297(3):R877-R884.
-
Leclair E et alii (2012). Faster pulmonary oxygen uptake kinetics in children vs adults due to enhancements in oxygen delivery and extraction. Scand J Med Sci Sports 22(4):1-8.
-
Stirling J, Zakynthinaki M (2009). Counterpoint: the kinetics of oxygen uptake during muscular exercise do not manifest time-delayed phases. J Appl Physiol 107(5):1665-7.
-
Cannon D et alii (2011). Skeletal muscle fatigue precedes the slow component of oxygen uptake kinetics during exercise in humans. J Physiol 589(3):727-39.
-
Lima Silva A, Oliveira F (2004). Consumo de oxigênio durante o exercício físico: aspectos temporais e aspectos de curvas. Rev Bras Cineantropom Desempenho Hum 6(2):73-82.
-
Krogh A, Lindhard J (1920). The changes in respiration at the transition from work to rest. J Physiol 53(6):431-9.
-
Hill A, Long C, Lupton H (1924). Muscular exercise, lactic acid, and the supply and utilization of oxygen. Proc R Soc (Biol) 96(679):438-75.
-
Margaria R, Edwards H, Dill D (1933). The possible mechanisms of contracting and paying the oxygen debt and the role of lactic acid in muscular contraction. Am J Physiol 106(3):689-715.
-
Castinheiras Neto A, Farinatti P (2009). Consumo de O2 após o exercício resistido: uma abordagem crítica sobre os fatores determinantes de sua magnitude e duração. Braz J Biomotr 3(2):96-110.
-
Bertuzzi R et alii (2010). Predicting MAOD using only a supramaximal exhaustive test. Int J Sports Med 31(-):477-81.
-
Behnke B et alii (2009). Recovery dynamics of skeletal muscle oxygen uptake during the exercise off-transient. Respir Physiol Neurobiol 168(3):254-60.
-
Castinheiras Neto A, Silva N, Farinatti P (2009). Influência das variáveis do treinamento contra-resistência sobre o consumo de oxigênio em excesso após o exercício: uma revisão sistemática. Rev Bras Med Esporte 15(1):70-8.
-
Matsuura C, Meirelles C, Gomes P (2006). Gasto energético e consumo de oxigênio pó-exercício contra-resistência. Rev Nutr 19(6):729-40.
-
Marques Junior N (2012). Matemática da cinética do VO2 e da contribuição do sistema de energia durante o exercício. Rev Bras Prescr Fisiol Exerc 6(36):578-603.
-
Guimarães P (2001). Ajuste de curvas experimentais. Santa Maria: Editora UFSM. p. 49.
-
Schmidt Junior L (2010). Obtenção de equações de desempenho de difusores de ar. 28 f. Monografia de Engenharia Mecânica, UFRGS, Rio Grande do Sul.
-
Morettin P, Hazzan S, Bussab W (2010). Cálculo: funções de uma e várias variáveis. 2ª ed. São Paulo: Saraiva. p. 289-93.
-
Chuquipoma J (2012). Modelagem matemática. São João Del Rei: UFSJ. p. 28-41.
-
Custodio R, Andrade J, Augusto F (1997). O ajuste de funções matemáticas a dados experimentais. Quím Nova 20(2):219-25.
-
Pereira T M (2006). Cálculo numérico – função exponencial. RS: UNIJUÍ. http://www.projetos.unijui.edu.br/matematica/cn/ajuste_de_curvas.htm (acesso em 18/03/2012)
-
Guidorizzi H (2012). Um curso de cálculo. 5ª ed, vol 2. Rio de Janeiro: LTC. p. 351-9.
Outros artigos em Portugués
 |

Búsqueda personalizada
|
|---|---|
|
EFDeportes.com, Revista Digital · Año 18 · N° 180 | Buenos Aires,
Mayo de 2013 |
|