Xadrez na escola: relações entre o ensino-aprendizagem dessa ferramenta extracurricular e a educação


	Xadrez na escola: relações entre o ensino-aprendizagem dessa ferramenta extracurricular e a educação El ajedrez en la escuela: relaciones entre enseñanza-aprendizaje de esta herramienta extracurricular y la educación
	Graduada em Serviço Social na Universidade Estadual de Ponta grossa (UEPG) Especialização em Dependência Química *Graduado em Educação Física em Licenciatura/Bacharel pela Universidade Estadual do Centro Oeste, Pós graduando em Educação pela Faculdade de Educação de Prudentópolis, FACEPP. Professor de Educação Física da rede Estadual	Valeria Ferreira Correia* Audri Ieger Gruba Jean Damião Goloiuh** jheanpg@hotmail.com (Brasil)
	Resumo O xadrez como interface curricular e meio de aprendizagem pelo jogo é um dos métodos mais estudados nas aulas de Educação Física para possível auxílio do desenvolvimento interdisciplinar. Este estudo teve como pressuposto analisar e discutir quais são as interfaces do xadrez no auxílio da matemática e como esse jogo pode intervir diretamente na educação dos alunos. Essa pesquisa é de cunho qualitativo e recebe um olhar antropológico para melhor compreensão do mundo enxadrista. Participaram do estudo seis indivíduos dos quais praticam o jogo tanto fora quanto dentro do âmbito escolar. Esta pesquisa busca contribuir para uma maior compreensão de como o xadrez na escola pode contribuir no desenvolvimento integral dos alunos nas disciplinas curriculares. Unitermos: Jogo de xadrez. Matemática. Escola. Artigo apresentado como Trabalho de Conclusão de Curso, no Curso de Metodologia de Educação Física da Faculdade Internacional de Curitiba. FACINTER, 1-2010.
	EFDeportes.com, Revista Digital. Buenos Aires, Año 17, Nº 178, Marzo de 2013. http://www.efdeportes.com/

1 / 1

1.     Introdução

    Há mais de dois séculos, o alemão Johann Wolfgang Goethe (1749-1832) definiu o xadrez como sendo um “excelente exercício mental” e, desde então, vários estudos têm se ocupado de investigar a relação existente entre este jogo e o desenvolvimento da inteligência humana. Pelo fato da existência da natureza lúdica do homem, criou-se e desenvolveram-se diversos jogos que se assemelham aos aspectos da realidade social. Dentre todos os jogos, o xadrez tem certo prestígio por ser um jogo voltado para o desenvolvimento do raciocínio lógico, concentração e atenção (Rezende, 2005).

    Muito se fala sobre o jogo de xadrez e seus usos na educação, mas sua introdução no âmbito escolar exige a criação de algumas condições ainda não existentes em boa parte das escolas. Isso porque, muitas o têm utilizado como aparato extracurricular ou atividades ludo-terápicas nas aulas de Educação Física. Sem desconsiderar tais práticas, pretendo aqui apresentar a sua utilização sob outro prisma.

    Edward Lasker no seu livro História do Xadrez relata a mais conhecida história do surgimento desse jogo. A invenção é atribuída a Sissa, um brâmane da corte do rajá Balhait. Assim, essa história teria sido contada, pela primeira vez há mais de mil anos e dizia que certo rei pediu a um de seus sábios que criasse um jogo capaz de mostrar o valor de qualidades como a prudência, a diligência, a visão e o conhecimento, como forma de se opor aos sentidos fatalistas de outro jogo, o nard (gamão), cujos resultados eram decididos pela sorte. Sissa então apresentou ao rei Kaíde um tabuleiro de xadrez, não muito diferente do que conhecemos hoje, com quatro elementos que representavam o exército indiano, explicando-lhe que havia escolhido a guerra como modelo para o jogo porque ela era a escola mais eficiente no ensino e aprendizado de determinados valores, tais como: o valor da decisão, do vigor, da persistência, da ponderação e da coragem.

    O rei, diante de tanta complexidade, ficou encantado com o jogo e ordenou que fosse preservado nos templos, considerando seus princípios como o fundamento de toda justiça e sustentando que ele era o melhor treinamento na arte da guerra.

    A partir daí, o rei teria lhe oferecido uma recompensa que ela escolheria de livre arbítrio e Sissa teria pedido, diante da insistência do rei, a retribuição em grãos de milho distribuídos sobre o tabuleiro de xadrez da seguinte forma: “na primeira casa, um grão; na segunda, dois; na terceira, quatro; na quarta o dobro de quatro; e assim por diante, até a última casa”. (Lasker, 1999, p. 30). Contudo, ao ordenar que o pedido fosse realizado o rei se surpreendeu, afinal não seria possível realizar o pedido de Sissa, pois, antes mesmo de chegar à trigésima casa, todo milho da Índia teria se esgotado, cobrindo a camada da Terra com uma espessura de 9 (nove) polegadas. O número exato seria 18.446.744.073.709.551.615 (Dezoito Quintilhões, Quatrocentos e Quarenta e Seis Quatrilhões, Setecentos e Quarenta e Quatro Trilhões, Setenta e Três Bilhões, Setecentos e Nove milhões, Quinhentos e Cinqüenta e Um Mil, Seiscentos e Quinze) grãos de milho, ou 64 2 - 1. Desse modo, o rei ficou confuso, porque não sabia o quê exatamente tinha que admirar, a invenção do jogo ou a engenhosidade do pedido de Sissa. (op. cit., p. 30).

    De qualquer modo, e independente de suas origens, o jogo de xadrez tem múltiplos usos na educação escolar, entre as suas possibilidades, pode-se acrescentar a sua apresentação aos alunos como tema transversal, enriquecendo suas aprendizagens e permeando a prática educativa em diversas áreas ou mesmo inserindo-o como disciplina desde as séries iniciais. Em 20 de dezembro de 1996, a Lei n. 9.394, estabeleceu as diretrizes e bases da educação nacional, cujos artigos 26 e 27, incluem o xadrez nas escolas, na parte diversificada dos currículos e também na parte consagrada à promoção do desporto.

    O artigo 32 dispõe que o ensino fundamental terá por objetivo a formação básica do cidadão a partir do desenvolvimento de sua capacidade de aprender, tendo como meios básicos o pleno domínio da leitura, escrita e do cálculo, com vistas a:

II - a compreensão do ambiente natural e social, do sistema político, da tecnologia, das artes e dos valores em que se fundamenta a sociedade;

III - o desenvolvimento da capacidade de aprendizagem, tendo em vista a aquisição de conhecimentos e habilidades e a formação de atitudes e valores;

IV - o fortalecimento de vínculos de família, dos laços de solidariedade humana e de tolerância recíproca em que se assenta a vida social.

    Acredito que estes objetivos podem ser plenamente alcançados por meio da inserção do jogo de xadrez como disciplina escolar, desde que implantada no currículo das séries iniciais, começando ainda na Educação Infantil. Essa eficácia do jogo de xadrez e a influência que tem sobre o desenvolvimento e comportamento estudantil é algo que pode ser mensurado por pesquisas utilizadas no campo das ciências cognitivas.

    Essa pesquisa levou a campo um olhar antropológico e visa compreender como o xadrez (ferramenta pedagógica) auxilia nas multidisciplinaridades escolares, principalmente seu uso na matemática; estabelecer uma relação de aprendizagem entre alunos praticantes do jogo e não-praticantes; e demonstrar novas metodologias de inserção do xadrez como praticas pedagógicas.

2.     Desenvolvimento

2.1.     Métodos

2.1.1.     A pesquisa

    Seguindo os subsídios teóricos de Lüdke e André (1986, p. 13), que fazem uma discussão sobre a pesquisa em educação, dentro de uma vertente qualitativa, apresento aqui a base teórica da pesquisa desse tema voltado para um olhar antropológico seguido da pesquisa etnográfica. O uso dessa terminologia deve ser feito de maneira apropriada. De acordo com as referidas autoras, isso ocorre pelo fato de o termo etnografia ter se distanciado do seu sentido próprio – “é a descrição de um sistema de significados culturais de um determinado grupo” (LÜDKE E ANDRÉ, 1986, p. 13-4) – no processo de adaptação para a área de educação, sofrendo modificações.

    Um estudo voltado para questões educacionais que se utilize da etnografia deve ter o cuidado em refletir sobre o processo de ensino aprendizagem, situando-o dentro de um contexto sócio-cultural mais amplo. Deve haver a preocupação em não reduzir a pesquisa somente ao ambiente escolar, mas também promover uma relação entre o que se aprende na escola e o que se passa fora dela.

2.1.2.     Sujeitos

    Participaram da pesquisa 6 (seis) alunos, 4 (quatro) do sexo feminino e 2 (dois) do sexo masculino, devidamente matriculados no ensino fundamental correspondendo de forma alternada do 6º ao 9º ano (Lei nº 11.274). A faixa etária dos participantes é de 11 (onze) a 17 (dezessete) anos. Todos os participantes praticavam o xadrez a mais de um ano e faziam uso dessa ferramenta além do ambiente escolar.

2.1.3.     Técnica da pesquisa

    Fez-se uso da ótica antropológica através da interação e vivencia com a população pesquisada. Dentro dos objetivos a serem alcançados utilizou-se uma entrevista estruturada com questões fechadas relativas a dados pessoais. O acompanhamento multidisciplinar foi o ponto precípuo da pesquisa, pois relatou-se quais eram as formas em que o xadrez poderia auxiliar na matemática. A relação entre praticantes e não-praticantes da modalidade foi de suma importância para que algumas relações vinculadas a essa ferramenta metodológica pudesse ficar de forma mais clara. Para que a pesquisa se concretizasse foram realizadas aulas em que o xadrez era a ferramenta chave dos exercícios de matemática, com isso, o acompanhamento das aulas no decorrer do ensino estabeleceu de forma clara o avanço e desenvolvimento da disciplina.

2.1.4.     Local

    A pesquisa foi realizada em uma escola pública situada no Município de Teixeira Soares - Paraná. Essa Instituição adere o ensino fundamental e médio e tem por característica a formação de diversos enxadristas. A maioria deles aprendem o próprio jogo dentro desse ambiente. O xadrez como prática pedagógica nessa escola recebe atenção especial, pois o auxilio disciplinar e nas interações sociais é bem vista.

2.2.     Fundamentação teórica

2.2.1.     Maturação pelo xadrez

    O desenvolvimento da criança é um processo muito complexo. Verifica-se que na fase de estruturação da sua personalidade, a necessidade de tomar decisões, é um processo perturbador, gerador de inúmeras dúvidas e incertezas. A prática do Xadrez poderá contribuir de forma decisiva, para consolidar o nível de maturação, preparando os alunos para analisarem com rigor as implicações das suas decisões.

    A dinâmica da cooperação com os outros é outro dos benefícios do xadrez, tanto no seu estudo como na sua prática. O jovem é compelido a escolher as ações favoráveis ao êxito pessoal e do grupo, admitindo as indicações que o monitor ou professor lhe dirige e aceitando as opções e falhas dos seus colegas. A criança e o jovem têm de conhecer o objetivo do jogo, a função e o modo de execução das principais ações e as suas regras. Se o jovem adquire gosto pelo xadrez simultaneamente começa a desenvolver o raciocínio lógico e também a desenvolver habilidades de observação, reflexão, análise e síntese. A avaliação do processo de desenvolvimento da criança é sempre uma questão chave no contexto educativo em geral e no contexto da aprendizagem do xadrez em particular.

2.2.2.     O xadrez educativo

    O atual sistema de apoios educativos e mecanismos de recuperação de alunos revelam-se pouco funcionais e muitas vezes improdutivos. “De certo modo, dificuldades passam de uma geração a outra e constituem o pano de fundo da desculpabilização social e individual para o fenómeno do chamado ‘insucesso’ da matemática escolar” (Ponte, 1997). Existem competências e habilidades associadas à prática educativa do jogo de xadrez, que podem ser benéficas e (ou) transferíveis ao conjunto dos processos inerentes à formação integral dos alunos e professores nos níveis do ensino básico, secundário e até superior.Estudos teóricos e experiências realizadas em muitos países evidenciam que, em aulas educativas com base no xadrez, para além do sentido lúdico estrito do jogo, diversos aspectos podem ser explorados e trabalhados.

    O professor poderá recorrer a:

Aspectos históricos, culturais e artísticos: estudo da origem do xadrez, história, lendas e povos; biografias de personalidades praticantes do xadrez; o significado histórico e o sentido simbólico das peças e do tabuleiro; o designer das peças, o sentido estético de uma partida.

Socialização: o sentido democrático do xadrez considerando que pessoas diferentes em todos os sentidos (idade, sexo, condição social ou física, raça, religião, ideologia) podem interagir através do xadrez.

Matemática: princípios matemáticos de consistência, suficiência, e independência estão presentes na concepção das regras do xadrez. Também podem ser elaborados problemas associados a conteúdos como probabilidade, combinatória, geometria e álgebra.

Comportamento e conduta ética: a experiência de perder fomenta a reflexão do aluno sobre o erro e o modo de chegar ao acerto; saber ganhar e perder promovem a auto-estima; o crescimento só é possível pelo próprio mérito do aprendiz.

Criatividade: os desafios e diversidade presentes numa partida de xadrez estimulam a criatividade; simulações com problemas também podem ser feitas.

3.     Resultados e discussão

    De modo a estabelecer os resultados, verificou-se ao longo do ensino do xadrez que a melhora na disciplina de matemática foi evidente em todos os aspectos, como visto na Tabela de características pessoais dos participantes (Tabela 1).

Tabela 1. Dados pessoais e resultado da aplicação dos exercícios de xadrez

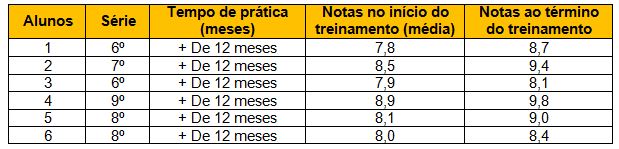
    A tabela acima demonstra alguns aspectos a serem considerados quanto às individualidades de cada participante. As notas de início foram consideradas pela média dos dois primeiros bimestres do ano letivo. As notas após a aplicabilidade dos exercícios são por meio da média dos dois outros bimestres. Não só as médias das notas demonstram que os alunos tiveram uma melhora, mas, a conversa informal com os professores de matemática adjuntos da pesquisa também levou a crermos que a melhora nas aulas foi significante.

    Para chegar a esses resultados, fez uso do método de ensino de PENA (2010) onde:

    O xadrez e a matemática são ciências exatas, ambas ricas em interdisciplinaridade, no qual, diversos conceitos enxadrísticos podem ser aplicados à matemática. Alguns deles são: estimativa, coordenadas cartesianas, valores absolutos, noções espaciais e de lateralidade, geometria, área e perímetro, probabilidade, estatística, problemas de lógica, progressão geométrica (PG), e vários outros. Nessa concepção, as aulas de xadrez na escola foram voltadas a exercícios de matemática. Com isso, houve o acompanhamento do aluno na disciplina de matemática e sua possível melhora. A seguir está descrita a programação de aula de xadrez na escola, que conta com uma sistematização.

Contagem e comparação de quantidades.

As quatro operações:

Adição: quando há ganho de material através das trocas.

Subtração: quando há perda de material através das trocas.

    Veja o diagrama à cima, por exemplo: Pretas jogam..... d5 x e4 - B x e4 B x e4 - C x e4 T x e4 (?) - T x e4

    E brancas possuem considerável vantagem material.

Multiplicação: quando uma peça aumenta o poder de outra, como por exemplo: dobrar as torres numa coluna aberta.

    No diagrama a cima branca joga: T(f1) d1 ..., dobrando as torres na coluna “d” e visando a casa d7 numa ameaça para as pretas, posicionando na 7ª fileira uma das torres brancas.

Divisão: quando as peças estão mal posicionadas ocorre a divisão de forças no tabuleiro. No diagrama ao lado, as peças brancas estão melhor posicionadas e as peças pretas “dividiram-se”, pois não dominam tantas casas como as peças brancas.

Figuras e movimentação geométricas das peças.

Quadrado.

Triângulo.

Várias figuras geométricas.

    Exemplos:

Bispos: diagonais

Torres: perpendicularismo/ortogonalidade

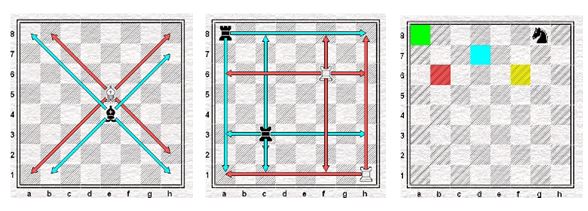
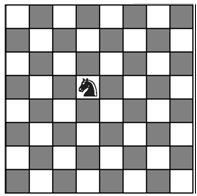
Caso interessante: o cavalo e o problema do seu percurso em todas as casas do tabuleiro. Este exercício consiste em percorrer utilizando o movimento do cavalo, todas as casas do tabuleiro sem repetir nenhuma já utilizada. No diagrama ao lado: f6, d7, b6, a8, depois pode continuar com c7, e6 (passando sobre a casa d7) o interessante é respeitar a regra: não repetir as casas que já foram utilizadas. Grandes pensadores matemáticos utilizaram este problema para ensinar probabilidades e análise combinatória.

Coordenadas algébricas sobre um plano cartesiano. Localização espacial em um plano

    Todos os diagramas utilizam “eixos cartesianos”. O eixo “x” é das fileiras numeradas. E o eixo “y” é o das colunas nomeadas da esquerda para a direita da letra “a” até “h” minúsculas.

Noção de tempo através do cálculo de lances

    Para um aluno realizar esta conta: 12 + 31 + 11 + 27 + 21 = ?, O aluno utiliza a calculadora para facilitar e utilizar menos tempo. Está correto? Mais ou menos. O ideal é o aluno trabalhar o cálculo mental para desenvolver o raciocínio. Por isso é bom evitar a utilização da calculadora ao realizar contas do dia a dia. No xadrez os cálculos ocorrem a todo o momento. Um exemplo comum que utilizamos a matemática para calcular lances, é nos finais de partida, principalmente nos finais de peões. Às vezes o enxadrista em um lance tem a possibilidade de ganhar a partida, mas depende de fazer um cálculo de vários lances para descobrir a linha vencedora.

Lateralidade

    Muitos alunos, especialmente nas fases introdutórias do ensino fundamental, possuem dificuldades na lógica e na compreensão sobre a lateralidade (sentido de direito e esquerdo). No jogo de xadrez a criança consegue aprender através do lúdico e do movimento das peças (especialmente torres, bispos e dama) os conceitos de horizontalidade, verticalidade, diagonais, bem como “esquerdo-direito”. Numa aula prática de xadrez, com o tabuleiro e as torres, os bispos e dama, rapidamente conseguem visualizar e traçarem os “caminhos” através de obstáculos.

    Vejamos um exemplo:

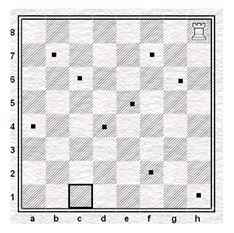
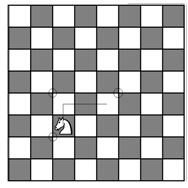
    Exercício com Torre: Respeitando o movimento da Torre, qual é o menor número de lances possíveis serão necessários para que a torre branca chegue a casa c1, sem passar por cima dos pontos pretos já indicados?

    Resp.: 3 lances (h3-c3-c1) Neste pequeno exemplo consegue-se visualizar alunos que possuem dificuldades de encontrar o melhor caminho para a torre, sendo assim gastarão maior número de lances possíveis. A solução proposta indica que o aluno possui os sentidos de horizontalidade e verticalidade aprendidos e aplicados no problema proposto.

Equações e problemas

    Grande parte do fracasso escolar em matemática deve-se a incompreensão de uma situação problema. Como transformar em linguagem matemática um enunciado e aplicar os conhecimentos de álgebra, geometria e aritmética como ferramentas na busca de uma solução? O xadrez podemos dizer que é um grande problema a ser resolvido. O enunciado é o seguinte: “Temos um exército branco e outro preto. Cada qual com 32 peças com seus movimentos e particularidades. Como dar xeque-mate no rei adversário?” Este é o problema central do xadrez e o desenvolvimento, o desenrolar do jogo dirige-se única e exclusivamente para este fim. Os jogadores elaboram planos, estratégias e metas a serem alcançadas para no fim conquistarem o seu objetivo maior: xeque-mate no rei adversário.

    Se alunos conseguem visualizar estes planos e estratégias, o jogo de xadrez pode e deve oferecer os passos para a solução de situações problemas do dia-a-dia utilizando os conceitos matemáticos para resolvê-los.

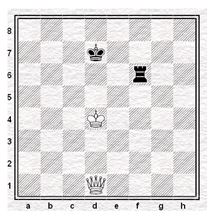
    Situação-problema: pretas movem e vencem. Análise da situação: as brancas possuem larga vantagem e facilmente vencem as pretas. Mas as pretas possuem um lance decisivo que mudará o fim deste jogo. Qual é o melhor lance? E com qual peça deverá mexer o condutor das peças pretas? Esta decisão é de extrema importância para a compreensão não somente do jogo, mas de situações matemáticas em que envolvem conceitos para a encontrar a solução dos mesmos. A resposta deste exercício é 1.... Td6 + (torre preta move-se para a casa d6 e dá xeque ao Rei branco). E porque este lance é o vencedor? Pois pela análise descobre-se a impossibilidade de o Rei branco sair do xeque e capturar a Torre preta que por sua vez capturará seguramente a Dama branca.

4.     Conclusão

    Durante muito tempo o ensino de matemática caracterizou-se por apresentar regras e procedimentos mecânicos, sem apelar para compreensão dos porquês de tais regras e procedimentos. Infelizmente, isso não é um fato apenas do passado; ainda hoje, o aluno tem que memorizar informações e resolver exercícios de forma mecânica, cuja função é a de reproduzir um conhecimento sem compreensão, não oportunizando a ele a construção de seu próprio saber. Pensando nestas questões, procura-se aqui apresentar subsídios para construção do conhecimento matemático de forma prazerosa, utilizando o jogo de xadrez. O jogo de xadrez para a matemática pode ser explorado convidando o aluno a participar, emitir opiniões e, ao mesmo tempo, o encorajar a usar uma variedade de habilidades, como classificação, seriação, levantamento de hipóteses, interpretação e formulação de problemas. O Xadrez e a Matemática são ciências exatas, ambas ricas em interdisciplinaridade.

    Na matemática identifica-se uma conexão intrínseca com todas as demais áreas do conhecimento humano, proporcionando ao aluno a capacidade de resolver problemas genuínos, gerando hábitos de investigação e propiciando uma visão ampla e científica da realidade. Diversos são os conceitos e relações entre o jogo de xadrez e a Matemática. Pode-se citar, por exemplo: reconhecer e apreciar a presença das formas na natureza e nos objetos produzidos pelo homem, a compreensão espacial para interpretar, compreender e apreciar o nosso mundo, o qual é intrinsecamente geométrico. A prática do jogo de xadrez pode colaborar diretamente para o aperfeiçoamento e melhoria do processo ensino-aprendizagem da Matemática.

    Seguindo o pressuposto desse trabalho, verificou-se longo do ensino do xadrez que a melhora na disciplina de matemática foi evidente em todos os aspectos. Isso foi alcançado tanto pela análise dos professores adjuntos da pesquisa quanto às avaliações aplicadas ao final da pesquisa com os exercícios. Por mais que os alunos já praticavam o xadrez antes, ficou evidente que os métodos e exercícios acima demonstrados fizeram a diferença para que a aprendizagem da disciplina de matemática e a melhora no entendimento da mesma pudessem ocorrer. Isso se deu pela análise das notas comparativas entre o início e o término das atividades.

Programa de exercícios aplicados nas aulas de xadrez para possível auxilio na matemática

    Estes exercícios de matemática que envolvem o tema ”Xadrez” têm por objetivo utilizar o xadrez na matemática visando trabalhar o interesse dos alunos e dessa forma, contribuir para o aprendizado despertando o fascínio pelas aulas de matemática. Os exercícios mostram além de tudo, como a matemática e o xadrez fazem uma parceria de sucesso. Ao elaborar os exercícios, os professores deverão substituir os nomes adequando-os aos seus alunos nos casos, fazendo assim, com que desperte ainda mais o interesse destes na resolução daqueles.

Exercícios de cálculo de áreas.

Calculando áreas em um tabuleiro de Xadrez.

OBS: Os exercícios envolvendo um tabuleiro de xadrez serão utilizados a medida oficial (40/40 cm).

1)     Calcule a área total de todas as casas brancas de um tabuleiro de Xadrez.

2)     Observe o diagrama abaixo e calcule a área total de todas as casas ocupadas por peças.

3)     Calcule a área total da parte mais importante do tabuleiro, conhecido como o

“quadrado central”.

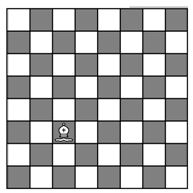
4)     No diagrama abaixo, temos um peão localizado na casa “e2”, observe as casas onde este peão ataca e calcule a área total das casas atacada pelo peão.

5)     Neste diagrama abaixo, observe que temos uma determinada posição. Calcule a área total de todas as casas que os peões das brancas atacam.

6)     Temos neste diagrama abaixo uma torre localizada na casa “e4”, calcule a área total das casas onde esta torre ataca.

7)     Observe que temos um bispo localizado na casa “c3”. Calcule a área total das casas atacadas pelo bispo.

8)     Vejamos no diagrama abaixo a peça mais poderosa do Xadrez (dama) que está localizado na casa central “e4”. Calcule a área total de todas as casas onde ela ataca.

9)     Veja no digrama abaixo a peça mais importante do Xadrez (rei ) que está localizada na casa “d4”. Observe e calcule a área total de todas as casas onde este rei ataca.

10)     Temos na casa “d5” o cavalo. Observe o diagrama abaixo, quais são as casas que este cavalo ataca. Calcule a área total das casas atacadas pelo cavalo.

11)     Qual é a área total das casas b3, c8, f7, h1 e a2.

12)     Descubra nesta posição mostrada no diagrama abaixo, qual é a área em metros quadrado das casas onde se encontram as torres?

13)     Neste diagrama abaixo, todas as peças estão em suas casas de origem, descubra quais são as possibilidades que as brancas têm para jogar em seu 1º lance e depois calcule a área total destas casas.

14)     Calcule a área total do triângulo formado pelo movimento do cavalo que estava na casa”c3” e foi movimentado para casa “e4”, Observe no diagrama que os círculos mostram os vértices do triângulo das casas por onde o cavalo passou em seu movimento.

Vértice A, esta localizado na casa “c3”

Vértice B, esta localizado na casa “c4”

Vértice B, esta localizado na casa “e4”

Exercícios de Razão e Proporção:

18)     O enxadrista Gérson durante o ano de 2004, ganhou 2 torneios dos 7 disputados. Já o enxadrista Molina no mesmo ano ganhou 8 torneios de “x” torneios disputados Qual é a Razão entre o numero de torneios disputados entre os dois enxadristas?

19)     O enxadrista Rui disputou 12 torneios no ano de 2005 e obteve 48 vitórias. Qual a razão entre o número de vitórias para o número de torneios disputados por Rui?

20)     Em um torneio de xadrez na cidade de Varginha, participaram os 12 enxadristas convidados pela organização (Torneio fechado), onde apenas 4 se classificariam para disputar o título de Campeão Absoluto da cidade de Varginha do ano de 2000. Qual é a Razão entre o número de enxadristas pelo número de vagas para final?

Exercícios de Porcentagem.

21)     João Paulo disputou no ano de 2005, 74 partidas em torneios. João obteve 49 vitórias, 18 empates e 7 derrotas. Qual foi o aproveitamento de João Paulo em 2005?

22)     A Federação Mineira de Xadrez no ano de 2004, fechou o ano com 360 enxadristas com Rating FMX. A Federação observou que 25% desses enxadristas tinham Rating

FIDE. Dos restantes dos jogadores, 11 enxadristas tinham Rating CBX. Quantos jogadores tinham apenas Rating FMX?

23)     Na loja virtual do Clube de Xadrez o tabuleiro e peças oficiais são vendidos no valor de R$ 40 reais. Na compra de 10 jogos de peças o desconto é de 15% no total da compra. Ao fazer o pagamento o comprador Alexandre pagou 40% do pedido e o restante foi pago pela Academia de Xadrez. Qual foi o valor pago pela Academia?

Exercício que envolve Porcentagem e Áreas.

24)     O enxadrista Arthur pegou um tabuleiro de papelão durante a aula de Matemática que tinha as medidas oficiais (40/40 cm) e cortou em 4 partes iguais. Arthur mostrou para sua Professora de Matemática o tabuleiro cortado em 4 partes. A Professora pegou uma parte deste tabuleiro e pediu para que todos os alunos calculassem 75% da área total das casas brancas. Qual é a área em cm²?

Exercícios de Inequações.

26)     Em um torneio realizado em Uberaba, Francisco sagrou-se Campeão diante de “X” jogadores inscritos A organização do evento retirou 50 enxadristas que fizeram a inscrição, mas não estavam em dia com a LUX. A quantidade de enxadristas que restaram no torneio é menor que ¾ do total inscritos. Qual é a sentença matemática que podemos escrever para expressar esse fato? Quantos enxadristas participaram deste torneio?

Exercícios de lógicas.

27)     Em um torneio realizado em Araxá arbitrado pela Professora Andrea, classificarão três enxadristas para disputa do título. Márcio, Alexandre e Marco Antonio. Os três enxadristas confrontaram entre eles em apenas um turno. Após o termino do evento Márcio sagrou se campeão com 0.5 pontos a frente de Alexandre e Marcos terminou em 3° lugar com apenas 0.5 ponto. Nesta disputa tivemos apenas um único empate. Independente de cor, quais foram os três resultados do torneio?

Referências bibliográficas

BRASIL. Ministério da Educação e do Desporto. Secretaria da Educação Fundamental. Referencial Curricular Nacional para a Educação Infantil. Brasília. MEC/SEF, 2000; 3V.

BRASIL. Ministério da Educação e do Desporto. Secretaria da Educação Fundamental. Parâmetros Curriculares Nacionais. Brasília. MEC/SEF, 2000.

LÜDKE, Menga e ANDRÉ, Marli E. D. A. Pesquisa em educação: abordagens qualitativas. São Paulo: EPU, 1986.

LASKER, Eduard.Historia do xadrez. IBRASA. 1999. São Paulo.

PENA, A. Interdisciplinaridade do xadrez com a matemática. 2010. São Paulo

REZENDE, Sylvio. Xadrez pré-escolar: uma abordagem pedagógica. Rio de Janeiro: Editora Ciência Moderna Ltda. 2005.

Outros artigos em Portugués

	Búsqueda personalizada
EFDeportes.com, Revista Digital · Año 17 · N° 178 \| Buenos Aires, Marzo de 2013 © 1997-2013 Derechos reservados