Introducción
La educación actual se considera como un proceso que se inicia y continúa por
el propio esfuerzo del educando, y requiere de instrumentos y técnicas idóneas
para la actividad natural del aprendizaje no se atrofie. El maestro con guía
debe desarrollarle habilidades tanto físicas como mentales que lo preparen para
la vida que le corresponde vivir en el nuevo siglo.
En consecuencia, la formación es el proceso y el resultado cuya función es
preparar al hombre en todos los aspectos de su personalidad. La instrucción es
el proceso y el resultado cuya función es formar a los hombres en una rama del
saber humano, de una profesión. Requiere además y como resultado de esa misma
apropiación, que desarrolle todas sus facultades o potencialidades funcionales,
tanto espirituales como físicas.
En el estudiante hay que lograr además del proceso de la instrucción, la
formación de valores y sentimientos propios del hombre como ser social. La
sociedad es un devenir histórico acumulado valores morales, religiosos,
políticos y jurídicos, entre otros, que forman parte de los elementos más
preciados de su cultura.
Los avances de la ciencia y la tecnología en la actualidad reclaman
constantemente como necesidad del desarrollo de las tendencias sintéticas del
conocimiento una imbricación tal, que pueda vertebrar en un todo único, siendo
sólo posible asimilarlos cuando en el proceso de producción de conocimientos
está incorporada, de manera intencionada, una preparación actual capaz de
enfrentar el desafío de los nuevos tiempos.
La elevación de la calidad del aprendizaje de los estudiantes constituye un
objetivo fundamental de la educación en el socialismo y es, por tanto una de
las más importantes tareas que deben impulsar y desarrollar todos los
educadores en nuestro país.
Como es conocido, el proceso de enseñanza requiere de una gran organización y
capacidad del colectivo pedagógico para lograr atender eficientemente las
inclinaciones y potencialidades individuales de los estudiantes, sin que afecte
el carácter social de nuestra escuela que da iguales posibilidades a todos los
estudiantes. Para ello es preciso tratar en detalles las principales
características y principios que regulan la actividad cognoscitiva de los
alumnos y, lo más importante, profundizar en las múltiples oportunidades que
en este sentido tiene el profesor para realizar una labor afectiva que le
permite brindar una atención científicamente concebida a las diferencias
individuales, a la afectiva formación de hábitos y habilidades.
La relación interdisciplinaria ha sido definida por varios autores, entre ellos
Piaget la define como un intercambio mutuo y recíproco entre varias ciencias y
da como resultado un enriquecimiento recíproco.
Durante el Tercer Congreso de la FEU nuestro Comandante en Jefe Fidel Castro,
trazó las líneas estratégicas para el desarrollo de la Educación Superior y
donde señaló como objetivo central de este subsistema para la etapa venidera,
lo relativo a la calidad en la formación de los profesionales que demanda el
país y donde apuntó:
“Para ello será necesaria la adecuada integración de la enseñanza, la
ciencia y la producción, basándonos en nuestras propias realidades y
experiencias, sin desconoces la experiencia universal”.
Desarrollo
Este trabajo en el primer y segundo año de la carrera de Cultura Física en
todas las modalidades, tomando como base el objetivo de las asignaturas que
prepara a los estudiantes para resolver problemas sencillos y parciales de la
carrera donde los estudiantes deben ser capaces de aplicar las técnicas y
procedimientos relacionados con la organización, presentación e
interpretación de los datos primarios vinculados con un problema de la Cultura
Física con principios científicos, que le permita organizar, escribir y
analizar la información estadística para tomar decisiones, utilizando las
técnicas computarizadas.
Por todo lo antes expuesto se determinó que existen limitaciones como:
-
Aún
se evidencian insuficiencias en la preparación científico-metodológica de
los profesionales para el uso de la aplicación de la Matemática y el
Análisis de Datos.
-
Los
materiales elaborados por al Universidad de Ciencia y el Deporte en la
Cultura Física para la organización y desarrollo del proceso de enseñanza
aprendizaje y consultas no cuenta con un glosario de los términos
matemáticos –estadísticos.
Teniendo en cuenta el análisis realizado anteriormente de deriva el problema
científico: ¿Cómo favorecer la interpretación de los términos técnicos
de las asignaturas Matemática y Análisis de Datos para los profesionales de la
Cultura Física? En correspondencia del problema planteado se propone como objetivo:
Elaborar un glosario de los términos matemáticos y estadísticos para su
interpretación por parte de los profesionales de Cultura Física de la Facultad
Holguín.
Se emplearon métodos teóricos: el histórico-lógico, análisis-síntesis, la
inducción-deducción y empíricos: la entrevista y la encuesta.
El glosario está estructurado por los diferentes términos de las Asignaturas
Matemática y análisis de Datos con su significado interpretación y forma de
aplicación.
A continuación relacionamos algunos ejemplos de cada asignatura:
Glosario
de términos estadísticos
Al
Azar o Aleatorio:
randomness, random
Son todos aquellos eventos fortuitos o productos de la suerte.
Aleatoriamente:
randomly
Actividades o métodos producidos o llevados a cabo simulando un comportamiento
al azar.
Clase:
class
Subdivisión de escala de datos.
Correlación:
correlation
Cuando dos fenómenos sociales, físicos o biológicos crecen o decrecen de
forma simultánea y proporcional debido a factores externos, se dice que los
fenómenos están positivamente correlacionados. Si uno crece en la misma
proporción que el otro decrece, los dos fenómenos están negativamente
correlacionados. El grado de correlación se calcula aplicando un coeficiente de
correlación a los datos de ambos fenómenos. Una correlación positiva perfecta
tiene un coeficiente + 1, y para una correlación negativa perfecta es -1. La
ausencia de correlación da como coeficiente 0. Por ejemplo, el coeficiente 0,89
indica una correlación positiva grande, -0,76 es una correlación negativa
grande y 0,13 es una correlación positiva pequeña. (Correlación)
Cuartiles,
Deciles y Percentiles: quartile,
decile, percentile
Si un conjunto de datos está ordenado por magnitud, el valor central (o la
media de los dos centrales) que divide al conjunto en dos mitades iguales, es la
mediana. Extendiendo esa idea, podemos pensar en aquellos valores que dividen al
conjunto de datos en cuatro partes iguales. Esos valores denotados Q1,
Q2, y Q3, se llaman primer
cuartíl, segundo cuartíl
y tercer cuartíl, respectivamente.
EL Q2 coincide con la mediana.
Análogamente, los valores que dividen a los datos en 10 partes iguales se
llaman deciles, y se le denotan D1, D2,..., D9,
mientras que los valores que lo dividen en 100 partes iguales se llaman
percentiles, denotados por P1, P2,..., P99. El
5º decil y el 50º percentil coinciden con la mediana. Los 25º y 75º
percentiles coinciden con el primer y tercer cuartiles.
Colectivamente, cuartiles, deciles y percentiles se denominan cuartiles.
Curva
Normal: normal,
Bell curve
La forma prevista de la distribución normal.
Datos:
data
Son los valores cualitativos o cuantitativos mediante los cuales se miden las
características de los objetos, sucesos o fenómenos a estudiar.
Desviación:
deviation
Diferencia entre un valor y otro valor medio o típico. (Desviación
Media)
Desviación
Típica:
standard deviation
La desviación de un elemento del conjunto es su diferencia con respecto a la
medida; por ejemplo, en sucesión x1, x2, ..., xn
la desviación de x1 es x1-x, y el cuadrado de la
desviación es (x1- x )2. La varianza es la medida del
cuadro de las desviaciones. Por último, la desviación típica, representada
por la letra griega sigma (s), es la raíz cuadrada de la varianza, y se calcula
de la siguiente manera:
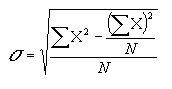
Si la desviación típica es pequeña, los datos están agrupados cerca de la
media; si es grande, están muy dispersos.
Es una mediada de dispersión expresada por el espacio de la curva normal
comprendido entre la media y 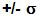 .
.
Entrevista
y Encuesta: interview, survey, poll
Son métodos de recolección de datos, la entrevista es una serie de preguntas
realizadas personalmente y la encuesta es llevada a cabo generalmente a través
de algún formulario que la persona debe llenar.
Estadística:
statistics
La Estadística estudia los métodos científicos para recoger, organizar,
resumir y analizar datos, así como para sacar conclusiones válidas y tomar
decisiones razonables basadas con tal análisis.
En un sentido menos amplio, el término estadística se usa para denotar los
propios datos, o número derivados de ellos, tales como los promedios. Así se
habla de estadística de empleo, estadística de accidentes.
Estadístico:
statistic
Unidad de medida referente a la muestra. Se le llama estadístico también a la
persona que trabaja con la estadística.
Frecuencia:
frequency
Número de veces en que se repite un dato.
Frecuencia
Acumulada: cumulative frequency
Es el número de estudiantes con calificaciones iguales o menores que el rango
de cada intervalo sucesivo. (Frecuencia)
Frecuencia
Relativa: relative frequency
Es la proporción entre la frecuencia de un intervalo y el número total de
datos.
Histograma:
histogram
Es una serie de rectángulos con bases iguales al rango de los intervalos y con
área proporcional a sus frecuencias.
Inferir:
to infer
Es emitir juicios o conclusiones basados en algún conocimiento o experiencia
sobre un evento o suceso.
Inferencia
Estadística: statistical inference
Es aplicar resultados de estudios de una muestra a las poblaciones y emitir
juicios o conclusiones sobre esa población en general. (Estadística)
Ejemplo:
Causas de la deserción estudiantil
en la Universidad.
Población:
4000 alumnos.
Muestra:
10% de la población.
Resultados
del Estudio de la Muestra: La situación económica, dificultad en el
aprendizaje.
Conclusiones:
Se puede
inferir que las causas de deserción de los alumnos de la Universidad son la
situación económica y la dificultad en el aprendizaje
Intervalo
de Clase: class interval
Pequeña sección de la escala según la cual se agrupan las puntuaciones de una
distribución de frecuencia. Tamaño o rango de la Clase.
Límites
del Intervalo: interval limits
Son los valores extremos que tiene el intervalo de clase, inferior y superior,
entre los cuales van a estar los valores de los datos agrupados en ese intervalo
de clase.
Media
Aritmética: arithmetic mean
La media de un conjunto de N números, X1, X2, X3,
.. XN. Se define por:
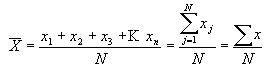
-
(Propiedades
de la Media Aritmética)
-
(Relación
Empírica entre Media, Mediana y Moda)
-
(Media
Armónica H)
-
(Media
Geométrica G)
-
(Relación
entre las Medias Aritmética, Geométrica y Armónica)
Media
Aritmética Ponderada: weighted
arithmetic mean
A veces asociamos con los números X1, X2, X3,
.. Xk ciertos factores peso (o pesos) W1, W2, W3,
.. WK dependientes de la relevancia asignada a cada número. En tal
caso,
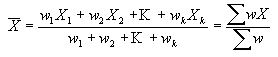
Se llama la media aritmética ponderada con pesos f1, f2,
..., fk.
Ejemplo: Si el examen final de un curso cuenta tres veces más que una
evaluación parcial, y un estudiante tiene calificación 85 en el examen final y
70 y 90 en los dos parciales, la calificación media es:
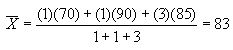
Propiedades
de la Media Aritmética
-
La suma algebraica de las desviaciones de un conjunto de números respecto
de su media aritmética es cero.
-
La suma de los cuadrados de las desviaciones de un conjunto de números
Xj
respecto de un cierto número "a" es mínima si y sólo si 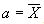
SI f1
números tienen media m1, f2 números tiene m2,...,fk números tienen media
mk,
entonces la media de todos los números es,
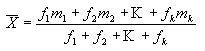
Es
decir, una media aritmética ponderada de todas las medias.
-
Si
A es una media aritmética supuesta o conjeturada (que puede ser cualquier
número) y si dj= Xj- A son las desviaciones de Xj respecto de A, las ecuaciones
(1) y (2) se convierten, respectivamente, en
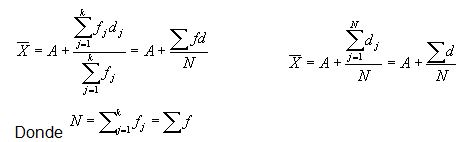
Mediana:
median
La
mediana de un conjunto de números ordenados en magnitud es o el valor central o
la media de los dos valores centrales.
Ejemplo:
El conjunto de números 3,4,4,5,6,8,8,8 y 10 tiene mediana 6. Ejemplo: El
conjunto de números 5,5,7,9,11,12,15 y18 tiene mediana.
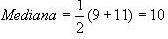
Para
datos agrupados, la mediana obtenida por interpolación viene dada por:

Geométricamente
la mediana es el valor de X (abscisa) que corresponde a la recta vertical que
divide un histograma en dos partes de igual área. Ese valor de X se suele
denotar por
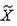 .
(Relación
Empírica entre Media, Mediana y Moda)
.
(Relación
Empírica entre Media, Mediana y Moda)
Medidas
de la Dispersión: measures of
dispersion
Normalmente
la estadística también se ocupa de la dispersión de la distribución, es
decir, si los datos aparecen sobre todo alrededor de la media o si están
distribuidos por todo el rango. Una medida de la dispersión es la diferencia
entre dos percentiles, por lo general entre el 25 y el 75. El percentil r es un
número tal que un r por ciento de los datos son menores o iguales que r . En
particular, los percentiles 25 y 75 se denominan cuartiles inferior y superior
respectivamente. La desviación típica es otra medida de la dispersión, pero
más útil que los percentiles, pues está definida en términos aritméticos
como se explica a continuación.
Medidas
de Tendencia Central: measures of
central tendency
Un
promedio es un valor típico o representativo de un conjunto de datos. tales
valores suelen situarse hacia al centro del conjunto de datos ordenados por
magnitud.
Una
vez que los datos han sido reunidos y tabulados, comienza el análisis con el
objeto de calcular un número único, que represente o resuma todos los datos.
Dado que por lo general la frecuencia de los intervalos centrales es mayor que
el resto, este número se suele denominar valor o medida de la tendencia
central.
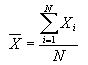
Sean X1,X2,...,Xn los datos de un estudio estadístico. El valor utilizado mas a
menudo es la media aritmética o promedio aritmético que se escribe X, y que es
igual a la suma de todos los valores dividida por n.
El
símbolo 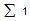 o sumatoria, denota la suma de todos los datos. Si las X se
agrupan en K intervalos, con puntos medios m1,m2,..., mk y frecuencias
f1,f2,...,fk, la media aritmética viene dada por:
o sumatoria, denota la suma de todos los datos. Si las X se
agrupan en K intervalos, con puntos medios m1,m2,..., mk y frecuencias
f1,f2,...,fk, la media aritmética viene dada por:
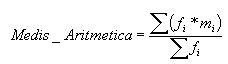 donde
i=1,2,...,k.
donde
i=1,2,...,k.
La
mediana y la moda son otros dos valores de la tendencia central. Si las x se
ordenan según sus valores numéricos, si n es impar la mediana es la x que
ocupa la posición central y si n es par la mediana es la media o promedio de
las dos x centrales. La moda es la x que aparece con mayor frecuencia. Si dos o
más x aparecen con igual máxima frecuencia, se dice que el conjunto de las x
no tiene moda, o es bimodal, siendo la moda las dos x que aparecen con más
frecuencia, o es trimodal, con modas las tres x más frecuentes.
Glosario
de términos matemáticos
-
Adición
: Operación matemática en la que se unen dos o más Cantidades
-
Acutángulo:
Triángulo que tiene sus tres ángulos agudos.
-
Álgebra:
Rama de la Matemática en la que se usan símbolos, letras y números para
expresar relaciones entre expresiones que representan números.
-
Algoritmo:
Descripción paso a paso de una solución de un problema
-
Aritmética
Es la parte de la Matemática que estudia los números y las operaciones hechas
con ellos.
-
Binomio:
Expresión algebraica de dos términos. Ejemplo, 5a - 2b.
-
Catetos:
Lados que forman el ángulo recto de un triángulo rectángulo.
-
Cero
de una función: Todo punto para el cual f(x) = 0.
-
Cifra
Significativa: Todas las cifras excepto el cero.
-
Conjunto
Infinito: Conjunto de un número ilimitado de
elementos.
-
Congruencia
(de figuras): Dos figuras son congruentes si tiene sus lados homólogos
congruentes.
-
Conmutativa:
Propiedad que no cambia el resultado de una operación al alterar el orden de
los elementos que operan.
-
Demostración:
Proceso por el cual, mediante una serie de razonamientos lógicos, se llega a
establecer la verdad de una proposición o teorema a partir de cierta
hipótesis.
-
Denominador:
Parte de una fracción que indica en cuántas partes está dividido un todo o la
unidad.
-
Descomposición
Factorial: Descomponer un número en sus factores primos.
-
Desigualdad:
Relación matemática que indica que dos expresiones no son iguales.
-
Diagonal:
Segmento rectilíneo que une dos vértices no consecutivos de una figura
geométrica.
-
Ecuación:
Es toda igualdad válida sólo para algún(nos) valor(es) de la(s)
variable(s). Ejemplo, 6x = 18; x - y = 7
-
Ecuación
cuadrática: Ecuación de segundo grado o cuadrática se expresa mediante
la relación ax2 + bx + c = 0, donde a es distinto de 0.
-
Ecuación
Trigonométrica: La ecuación trigonométrica es aquella cuyas
incógnitas son el asunto principal de las funciones trigonométricas.
-
Ecuaciones
equivalentes: Ecuaciones que tienen las mismas soluciones.
-
Equilátero:
Triángulo que tiene sus tres lados iguales.
-
Elemento:
Cada uno de los objetos pertenecientes a un conjunto.
-
Fracciones
Equivalentes: Aquellas que tienen el mismo valor.
-
Función
Lineal: Se define una función lineal con dos variables como una
expresión de la forma f(x, y) = ax + by. Su representación gráfica es una
recta.
-
Infinito:
Magnitud mayor que cualquier cantidad dada.
-
Inscrito
(Ángulo): Ángulo cuyo vértice está sobre una circunferencia y vale la
mitad del arco que subtiende.
-
Intersección:
Elementos comunes a dos o más conjuntos.
-
Líneas
Perpendiculares: Líneas que la cortarse forman un ángulo de 90°.
-
Logaritmo:
El logaritmo de un número, respecto de otro llamado base, es el exponente a que
hay que elevar la base para obtener dicho número.
-
Lugar
geométrico: Conjunto de puntos que cumple con una determinada
condición.
-
Número
complejo: Número de la forma a + ib con a y b, números
reales e i2 = -1.
-
Número
entero: El que consta exclusivamente de una o más unidades, por
oposición a los quebrados y los mixtos.
-
Número
fraccionario: Número que expresa una o varias partes de la unidad.
-
Número
imaginario: Número que resulta de extraer la raíz cuadrada de un
número negativo.
-
Número
impar: Número que no es divisible exactamente por dos.
-
Número
mixto: Número compuesto de entero y fracción.
-
Número
negativo: Número menor que 0.
-
Pirámide:
Cuerpo geométrico que tiene como base un polígono cualquiera y como caras
laterales triángulos con un vértice común.
-
Planos
Paralelos: Planos que no tienen ningún punto en común.
-
Raíz
Cúbica: Expresión radical de índice tres.
-
Razón:
Comparación entre dos cantidades por cuociente. Ejemplo, si un niño tiene 5
años y otro 3 años, decimos que sus edades están, respectivamente, en la
razón 5:3.
-
Recíproco:
Corresponde al valor inverso de un número, de manera tal que al efectuar el
producto entre ambos, resulta 1.
-
Recta:
Es la representación gráfica de una función de primer grado. Toda función de
la forma y = ax + b de IR en IR representa una línea recta.
Conclusiones
Una vez culminado el proceso investigativo se arriban a las conclusiones
siguientes:
-
Aunque existen varios autores que han realizado glosarios, hasta el momento
no se ha encontrado un trabajo completo que trate el tema, hecho que a
través de los mismos se hará el aporte de la investigación, por la
necesidad que presentan los profesionales de la Cultura Física de
identificarse con las asignaturas Matemática Básica y Análisis de Datos.
-
En el proceso enseñanza aprendizaje de la Matemática y el Análisis de
Datos en el primer y segundo año de la carrera de Cultura Física existen
posibilidades reales para que los profesionales logren familiarizarse con
los términos básicos de estas asignaturas.
Bibliografía.
-
Egaña Morales, E. La estadística herramienta fundamental en la investigación
pedagógica.
-
Glosario de Términos Matemáticos (2011) Soporte digital.
-
Guerra Bustillo. C. y col. (1987) Estadística. Ciudad de la Habana. Editorial
Pueblo y Educación.
-
Hoel, Paul G. Estadística elemental moderna.
-
Instituto Superior de Cultura Física. (2008)
Programa de la asignatura
Análisis de Datos. Versión 1. (En base de datos).
-
Jhon, E.F. (1977)
Estadística Elemental y Moderna. Ciudad de la Habana.
Editorial Pueblo y Educación.
-
Zatsiorki, V. M. (1989)
Metrología Deportiva. Ciudad de la Habana, Editorial
Pueblo y Educación.
Otros artículos sobre Educación
Física
 |
|
|
EFDeportes.com, Revista
Digital · Año 17 · N° 176 | Buenos Aires,
Enero de 2013
© 1997-2013 Derechos reservados
|

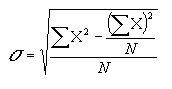
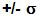 .
.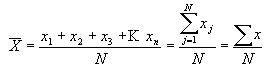
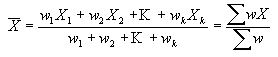
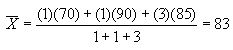
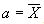
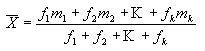
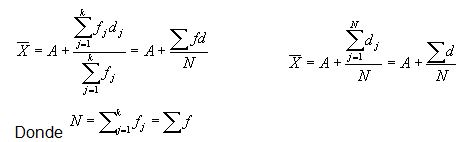
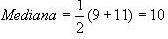

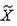 .
(Relación
Empírica entre Media, Mediana y Moda)
.
(Relación
Empírica entre Media, Mediana y Moda)
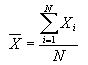
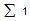 o sumatoria, denota la suma de todos los datos. Si las X se
agrupan en K intervalos, con puntos medios m1,m2,..., mk y frecuencias
f1,f2,...,fk, la media aritmética viene dada por:
o sumatoria, denota la suma de todos los datos. Si las X se
agrupan en K intervalos, con puntos medios m1,m2,..., mk y frecuencias
f1,f2,...,fk, la media aritmética viene dada por: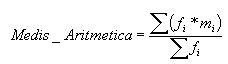 donde
i=1,2,...,k.
donde
i=1,2,...,k.