1 / 1

Introducción

    El hombre es una estructura dinámica que ocupa un lugar en el espacio y por ello es necesario localizarlo, situarlo de manera eficiente y rápida, utilizando planos y ejes (Hernández Corvo, 1990). “El sistema de referencia será necesario para especificar la posición del cuerpo, de un segmento o de un objeto, así como para describir si ocurren cambios en su posición” (Izquierdo, 2008). Se acepta universalmente un sistema cartesiano espacial con tres ejes de rotación denominados transversal, sagital y vertical, que permiten respectivamente el movimiento en tres planos denominados sagital, frontal y transversal (Guillen y Linares, 2002).

    Las articulaciones son los fulcros o apoyos principales de nuestras palancas anatómicas, a través de los cuales se puede considerar que pasan líneas rectas imaginarias que sirven de ejes de rotación de los diferentes segmentos anatómicos. Según Gardner (1971), la articulación es “la conexión existente en el esqueleto entre cualquiera de sus componentes rígidos, sean huesos o cartílagos”.

    En el codo, la articulación intermedia del miembro superior, se conectan tres elementos rígidos, los huesos húmero, cúbito y radio uniendo los segmentos anatómicos del brazo y del antebrazo. Es una estructura compleja, formada realmente por tres articulaciones separadas que comparten una cavidad sinovial común (Draque et al., 2007), estas son la húmero-cubital, la húmero-radial y la radio-cubital proximal. Las dos primeras permiten los movimientos de flexo-extensión en el plano sagital alrededor del eje transversal. El objetivo del presente trabajo es ofrecer una perspectiva analítica básica del movimiento de la articulación del codo, discusión que se plantea con fines didácticos en un sistema biaxial cartesiano en el que se conviene que su origen está ubicado en el punto de inserción del músculo bíceps braquial en el hueso radio, músculo que es el motor principal de la flexión cuando el antebrazo está supinado. Para facilitar el enfoque analítico de su movilidad, el plano cartesiano utilizado corresponde al plano sagital, el eje X de las abscisas corresponde al eje transversal y, el eje Y de las ordenadas corresponde al eje sagital.

Desarrollo

    Los huesos del codo y la flexión-extensión: “Las superficies del húmero se articulan con el conjunto cúbito-radio, permitiendo movimientos únicamente en el plano sagital” (Calais-Germain, 2004). La disminución de la relación espacial entre los segmentos anatómicos del brazo y del antebrazo, se denomina flexión y, está a cargo de las fuerzas que puedan efectuar tres músculos dependiendo de la actitud que asume el antebrazo: el bíceps braquial es el principal flexor en supinación, el braquial anterior en pronación y, el braquiorradial en posición neutra. El aumento de la relación espacial se denomina extensión y, está a cargo de la fuerza que puede efectuar el músculo tríceps braquial. En ambos casos se hace referencia a un gesto activo debido a la contracción del músculo agonista.

    Ángulo en posición normal: Es la relación espacial entre dos segmentos rectilíneos o rayos, denominados inicial y terminal. En la figura №1 se observa como el origen o vértice del “rayo inicial” (Ri) coincide con el origen del sistema de coordenadas y, su extremo está orientado positivamente sobre el semieje X positivo. A partir de este se mide el ángulo en el sentido contrario al movimiento de las agujas del reloj (antihorario) y se construye el rayo terminal (Rt) (Zill, Dennis y Dewar, 1999). La utilización conveniente de los rayos permite trasladar y orientar ángulos en otras zonas del plano cartesiano para hacer comparaciones. A continuación se representan ángulos en posición normal en los diferentes cuadrantes del plano cartesiano convencional:

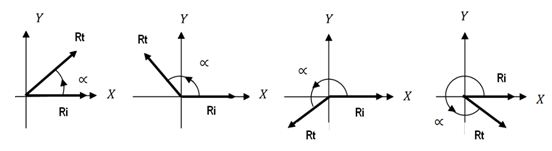
Figura 1. Ángulos en posición normal en los diferentes cuadrantes

    Para los movimientos articulares, el rayo terminal puede representar un vector denominado fuerza muscular y, representa el ángulo de tensión muscular que es simplemente la dirección en que se aplica dicha fuerza. Para el desplazamiento de las palancas anatómicas, los rayos pueden representar segmentos óseos que rotan alrededor de una articulación desde una posición a otra, describiendo un ángulo en posición normal denominado ángulo articular.

    La orientación de los ejes coordenados al considerar una posición específica del gesto articular puede ser muy diferente a la orientación de los ejes en el sistema cartesiano convencional (eje X horizontal y positivo hacia la derecha, eje Y vertical y positivo hacia arriba). Es así como el sentido antihorario podría generar confusión en la ubicación del ángulo en posición normal, razón por la que es conveniente de manera general ubicar positivamente el ángulo partiendo del semieje X positivo (sobre el cual se ubica el rayo inicial) y buscando por el camino más corto el semieje Y positivo hasta encontrar el vector (rayo terminal) que bien puede representar la fuerza muscular. Veamos dos ejemplos:

Figura 2. Ángulos en posición normal para diferentes orientaciones de los ejes

    Medición de ángulos: Los ángulos pueden medirse en grados o en radianes. “Un radián es un ángulo cuya longitud de arco es igual al radio del círculo” (Gutiérrez, 1999). Esto significa que si sobre una circunferencia tomamos una medida de longitud igual al radio, los rayos inicial y terminal determinan una relación angular igual a un radián (Figura №3a).

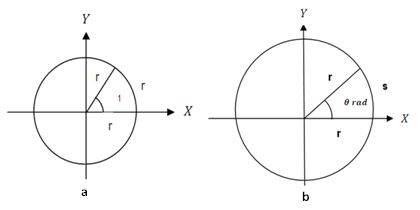
Figura 3. Referencia para la medición de ángulos: a. Un radián, b. Un ángulo genérico de θ radianes

    Sabiendo que radianes corresponden a una medida angular de 180°, utilizando una regla de tres simple se encuentra que 1 radian equivale aproximadamente a 57,3°. De modo que para convertir radianes a grados, basta con multiplicar por 57,3 y, para convertir grados a radianes, basta con dividir por 57,3.

    Como la longitud de la circunferencia es generada por un ángulo de , entonces por una regla de tres simple se puede determinar la fórmula general para calcular la longitud de arco s generado por un ángulo de (Figura 3b):

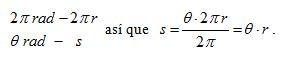
    La fórmula es muy importante en el movimiento articular humano porque refleja la optimización de los desplazamientos para realizar en forma eficaz las actividades cotidianas que requieren el concurso de las extremidades. Se conviene que en el gesto articular, representa el desplazamiento angular de todos los puntos de la palanca anatómica cuando el hueso pasa de una posición a otra y, s representa el desplazamiento lineal de un punto de la palanca ubicado exactamente a una distancia de unidades respecto al centro articular de rotación. Así, cuando un hueso efectúa una rotación alrededor de una articulación, desde una posición a otra, todos los puntos de la palanca anatómica realizan el mismo desplazamiento angular, pero diferente desplazamiento lineal, siendo mayor el desplazamiento lineal de los puntos más alejados de la articulación. Este concepto es de la mayor importancia en los gestos de locomoción para los miembros inferiores y superiores, donde se requiere aplicar una fuerza de mayor magnitud pero consiguiendo un desplazamiento lineal importante. “Estas palancas no ahorran la fuerza del que las utiliza…, sin embargo, incrementan la amplitud y la velocidad de movimiento del que las utiliza” (Pineda, 1997).

    Eje mecánico de un hueso: Es una línea recta imaginaria que pasa por los puntos medios de las superficies articulares del hueso. Esta definición se cumple para un hueso bi-articulado. No debe confundirse con el eje longitudinal del hueso, que se define como una línea curva imaginaria que pasa por las mitades de infinitos cortes transversales del hueso. Tampoco debe confundirse con el eje diafisiario que se orienta a lo largo de la diáfisis ósea.

    Cuando se trata de un hueso mono-articulado como en el caso de un segmento distal, el eje mecánico corresponde a una línea recta imaginaria que pasa por el punto medio de la superficie articulada y por el punto ubicado en el vértice de su extremo distal.

    En la figura №4 se esquematizan los ejes mecánicos de los tres huesos que componen la articulación del codo:

Figura 4. Ejes mecánicos de los huesos del codo: a. EM del húmero, b. EM del cúbito, c. EM del radio

    Se suele mencionar también el eje mecánico de un segmento anatómico, como por ejemplo el eje mecánico del brazo y el eje mecánico del antebrazo, por lo que se asume en este caso que se trata de una línea recta imaginaria que pasa por las mitades de las articulaciones que abarcan el segmento. Sin embargo, es más práctico considerar el eje mecánico del hueso, que es propiamente la palanca rígida que desea moverse en el gesto articular. Cuando se hable de eje mecánico del brazo, en realidad se hará referencia al eje mecánico del húmero y, cuando se hable de eje mecánico del antebrazo, se hará referencia al eje mecánico del radio.

    Nótese además que, como en el caso del húmero, el eje mecánico no tiene que cruzar por toda la diáfisis del hueso. Incluso en otros huesos como el fémur, el eje mecánico pasa casi completamente por fuera de la diáfisis.

    Ángulo articular: Es la relación espacial que hay entre los ejes mecánicos de dos huesos (o segmentos anatómicos) que se articulan. Se trata de un ángulo que forman instantáneamente dos huesos, por lo que no debe confundirse con el rango angular de movimiento, que es el conjunto de valores angulares que va describiendo una palanca anatómica desde su posición inicial o de referencia hasta una nueva posición de análisis.

    Los ángulos articulares o ‘joint angles” forman parte de un sistema que es utilizado por fisioterapeutas, anatomistas, y la comunidad médica, para definir las posiciones anatómicas de las articulaciones (Robertson et al., 2004). En este sentido, es razonable utilizar estos métodos para diagnosticar patologías del sistema locomotor y calificar la evolución de un paciente que se está rehabilitando.

    Amplitud de movimientos de la articulación del codo: Para Miralles (2002) el complejo articular del codo puede realizar dos movimientos, la flexoextensión y la pronosupinación, en asociación con la articulación radiocubital distal, donde asume como posición de referencia aquella en la cual el ángulo de 0° corresponde al momento en el que el eje del antebrazo está situado en la prolongación del brazo. Para una flexión activa generada por acción de los músculos agonistas, el rango de movilidad va, según Boone (1979) desde 0° hasta 141±4,9°, y según Petherick (1988), va desde 0° hasta 146±6,3°. En cambio, para una flexión pasiva, en la que la musculatura está relajada, el movimiento es causado por la acción de una fuerza externa, logrando un rango de movilidad que va desde 0° hasta 140-160°. Es claro entonces, que “el movimiento activo está limitado por el contacto de las masa musculares del brazo” (Molano, 2008). Para una extensión activa generada por la acción del músculo tríceps braquial, se considera el rango de movimiento a partir de un punto extremo de flexión hacia la posición de referencia, que en promedio es 150° a 0° (Hislop et al., 2002).

    Para mayor facilidad en el análisis, se recomienda hacer un esquema como el que aparece a la derecha de la figura №5, en el cual se utiliza una forma rectangular, que es la barra rígida representativa del segmento anatómico.

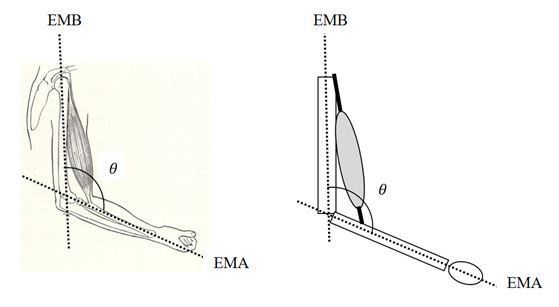
Figura 5. Ángulo articular en la flexión de codo por acción del músculo bíceps braquial. EMA: Eje mecánico del antebrazo, EMB: Eje mecánico del brazo, : Ángulo articular

    Línea de acción muscular: También llamada “línea de tensión muscular”, es una línea recta imaginaria que pasa por el punto de inserción muscular siguiendo la dirección del tendón. Sobre esta línea se representa el vector Fuerza Muscular. La línea de acción muscular no atraviesa necesariamente el centro del vientre muscular, incluso puede no tocarlo, como en el caso de la rodilla en una posición de flexión previa al gesto de extensión, en la que la línea de acción muscular del cuádriceps pasa por su punto de inserción en la tuberosidad tibial y se dirige a lo largo del tendón rotuliano sin tocar el músculo.

    Sobre esta línea se representa gráficamente el vector fuerza muscular del músculo o grupo muscular que con su contracción genera el gesto. La fuerza máxima que puede ejercer depende del área de su sección transversal, es decir, depende de dimensiones cuadráticas, su valor es aproximadamente (Cromer, 1992). 

    Esto significa que para ejercer una fuerza muscular de 30 kp durante una flexión de codo en supinación, el músculo bíceps braquial debe conseguir una sección transversal de .

    Ángulo de acción muscular: También llamado “ángulo de tensión muscular”, es la relación espacial que hay entre el eje mecánico y la línea de acción muscular (Figura №6). Este ángulo representa la dirección de la fuerza muscular en el sistema de coordenadas elegido para analizar el gesto articular, lo que permite discutir el significado de las componentes rectangulares de la fuerza. “En caso de participación muscular, el tamaño del ángulo de tensión muscular cambiará en cada grado del movimiento articular, y consecuentemente los tamaños de las componentes horizontal y vertical” (Luttgens y Wells, 1982).

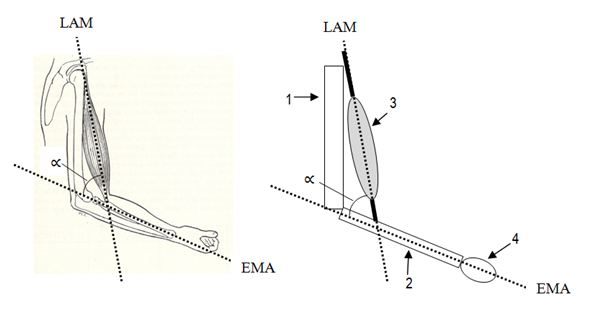
Figura 6. Ángulo de tensión muscular en la flexión de codo por acción del músculo bíceps braquial: 1. Palanca anatómica del brazo (Hueso Húmero) 2. Palanca anatómica del antebrazo 

(Huesos Cúbito y Radio) 3.Músculo Bíceps Braquial 4.Mano con la palma hacia arriba, : ángulo de tensión muscular, LAM: Línea de acción muscular del bíceps braquial, EMA: Eje mecánico del antebrazo

Sistema de coordenadas para el movimiento del codo

    Utilizaremos la siguiente convención (Ver Figura 7):

• Eje X: Es un eje paralelo al eje mecánico de la palanca anatómica del antebrazo (se asume el eje mecánico del hueso radio) que pasa por el punto de inserción muscular. Es positivo en el sentido que va desde el punto de inserción pasando por la articulación del codo.

• Eje Y: Es un eje perpendicular al eje mecánico de la palanca anatómica del antebrazo, por lo que también es perpendicular al eje X. Es positivo en el sentido del movimiento.

    Ambos ejes se cruzan en un punto que se caracteriza por tres perspectivas:

1. Anatómica: Punto de inserción muscular en el hueso de la palanca anatómica de la cual se estudia su desplazamiento. Específicamente, en la flexión del codo por acción del músculo bíceps braquial, su tendón se inserta en la tuberosidad bicipital del radio o, simplemente tuberosidad radial.

2. Matemática: Punto de intersección de los ejes X e Y, de coordenadas (0,0) que representa el origen del sistema.

3. Física: Punto de aplicación de la fuerza muscular que representa la potencia de la palanca anatómica.

    El vector Fuerza Muscular se representa sobre la línea de acción muscular haciendo coincidir su origen con el origen del sistema. En general se trata de un vector oblicuo (no paralelo a ninguno de los ejes) y por tanto, posee dos componentes rectangulares:

    Fmx: Componente de la fuerza muscular paralelo al eje mecánico de la palanca. No produce efecto rotatorio porque la prolongación de su línea de acción pasa por la articulación. Puede producir un efecto estabilizador con la tendencia a mantener articulado el hueso cuando se orienta positivamente (hacia la articulación), o un efecto luxador con la tendencia a desarticular el hueso cuando se orienta negativamente (alejándose de la articulación). En adelante, se hará referencia a Fmx como el “componente estabilizador” en el primer caso y, “componente luxador” en el segundo caso.

    Fmy: Componente de la fuerza muscular perpendicular al eje mecánico de la palanca. Produce efecto rotatorio que desplaza la palanca anatómica. En adelante, se hará referencia a Fmy como el “componente rotatorio agonista”. Cuando se analice el efecto negativo de una Fmy debido a la oposición de un músculo contra la acción principal, se llamará “componente rotatorio antagonista”.

    El ángulo de tensión muscular se mide como un ángulo en posición normal, partiendo del semieje positivo X y buscando el vector fuerza muscular por la trayectoria más corta (lo que corresponde en este sistema al sentido antihorario).

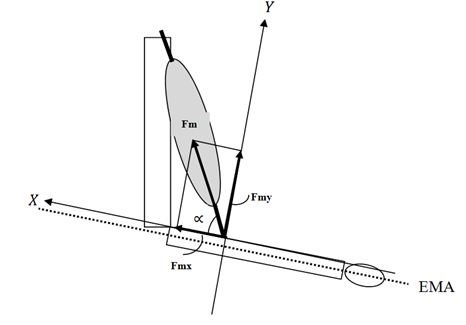
Figura 7. Sistema de coordenadas para el movimiento del codo: X = eje de las abscisas, Y = eje de las ordenadas, Fm = fuerza muscular, Fmx = componente 

de Fm paralelo al EMA, Fmy = componente de Fm perpendicular al EMA, = ángulo de tensión muscular, EMA: Eje mecánico del antebrazo

    Tomando el triángulo rectángulo auxiliar, observamos que:

Figura 8. Polígono de fuerzas: la fuerza muscular y sus componentes rectangulares

    Por la ley del polígono, podemos escribir vectorialmente:

    Por el Teorema de Pitágoras, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos y, podemos escribir escalarmente:

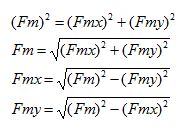
    Ecuaciones que sirven para calcular el valor de un lado, cuando se conocen los otros dos. Así, con la segunda ecuación puede calcularse el valor de la fuerza muscular cuando se conocen los valores de sus componentes, con la tercera puede calcularse el valor del componente paralelo al eje mecánico cuando se conocen los valores de la fuerza muscular y el del componente perpendicular al eje mecánico y, finalmente, con la cuarta puede calcularse el valor del componente perpendicular al eje mecánico, cuando se conocen los valores de la fuerza muscular y del componente paralelo al eje mecánico.

    En el mismo triángulo auxiliar, al ser rectángulo pueden aplicarse las funciones trigonométricas elementales:

    Dependiendo de los valores de cada par de parámetros conocidos, puede utilizarse una de estas ecuaciones para determinar el valor del parámetro desconocido. Por ejemplo: la primera de estas ecuaciones sirve para calcular el valor del componente perpendicular al eje mecánico cuando se conocen los valores de la fuerza muscular y su dirección, la segunda sirve para calcular el valor del componente paralelo al eje mecánico cuando se conocen los valores de la fuerza muscular y su dirección y, la tercera sirve para calcular la dirección cuando se conocen los valores de los componentes de la fuerza muscular, por medio de la función tangente inversa.

    Valores de la fuerza muscular: Varios factores determinan la acción gradual del músculo, de tal forma que pueda ejercer en diferentes momentos magnitudes distintas de fuerzas. González (1974) plantea tres argumentos: 1) el músculo para aumentar su fuerza, recluta más unidades motoras que sinergizan la fuerza total. 2) la frecuencia de impulsos que llegan a las unidades motoras aumentan la fuerza pero sin llegar a una respuesta tetánica. 3) en caso de requerir un valor máximo de fuerza, varias unidades motoras deben llegar a frecuencias tetánicas.

    Es recomendable que en el músculo se generen respuestas contráctiles de diferentes magnitudes dependiendo de las cargas que deba vencer, pero de manera gradual dentro de los límites elásticos de deformación transitoria.

    Momento de torsión (Torque): El efecto rotatorio de una fuerza se representa por la letra griega τ y, se define matemáticamente como el producto de la fuerza por la distancia perpendicular entre la línea de acción de dicha fuerza y el punto que representa el centro de rotación. También puede definirse como el producto del componente de la fuerza que es perpendicular al eje mecánico de la palanca y la distancia entre el punto de aplicación de dicha fuerza y el punto que representa el centro de rotación. “En lo que respecta a los movimientos de rotación o moción, el momento o momento de torsión desempeña la misma función que lleva a cabo la fuerza para un movimiento en una línea recta: es el tamaño del momento lo que aumenta o disminuye la velocidad angular de un cuerpo, y de este modo produce aceleración o deceleración del movimiento rotatorio’ (Gowitzke, 1999).

    El torque es un vector perpendicular al plano formado por la fuerza F y la distancia d, cuyo signo obedece a la regla de la mano derecha o, simplemente, asumiendo como positivo el sentido antihorario en el que el vector busca el centro de rotación por la vía más corta y, como negativo el sentido horario en el que el vector busca el centro de rotación por la vía más corta (Figura №9). En general, para una fuerza oblicua ocurre lo siguiente:

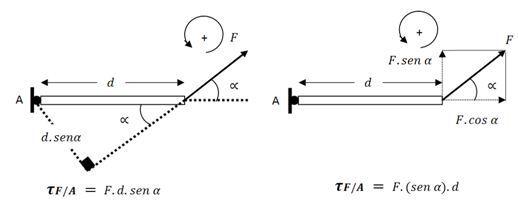
Figura 9. Torque de una fuerza respecto a un punto por donde pasa el eje de rotación

    El torque de una fuerza oblicua se puede calcular de dos formas:

1. Determinando el signo según lo convenido y multiplicando el valor de la fuerza por la distancia perpendicular que hay desde el centro de rotación hasta la línea de acción de la fuerza.

2. Determinando el signo según lo convenido y multiplicando el valor del componente de la fuerza perpendicular al eje mecánico por la distancia que hay entre el centro de rotación y el punto de aplicación de la fuerza.

    El símbolo τF/A se lee “el torque de la fuerza F respecto al centro de rotación A”.

    Cuando la fuerza F es perpendicular al eje mecánico de la palanca, se tiene y , por lo que

    Observe que cuando la fuerza F es oblicua, el torque es el mismo torque de su componente perpendicular al eje mecánico.

    Cuando la fuerza F está sobre el eje mecánico de la palanca, se tiene α = 0° y sen 0° = 0, por lo que τF/A = 0. Así que, todas aquellas fuerzas cuyas líneas de acción pasen por el centro de rotación, no producen torque.

Condiciones de equilibrio

    Diferentes problemas biológicos relacionados con el movimiento de las articulaciones, se consideran dentro de la estática cuando la fuerza total y el torque total sobre el sistema son nulos, es decir, “cuando el sistema no presenta aceleración lineal ni aceleración angular” (Herrera, 2001). Las condiciones de equilibrio o estaticidad se pueden expresar matemáticamente como sigue:

1. Primera condición de equilibrio: La sumatoria de todas las fuerzas que actúan sobre el cuerpo es nula. Simbólicamente: 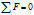, lo que equivale a la sumatoria nula de las fuerzas en los tres ejes coordenados del espacio

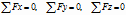
2. Segunda condición de equilibrio: La sumatoria de todos los torques de las fuerzas que actúan sobre el cuerpo con respecto a un punto específico del sistema, es nula. En nuestro caso se elige el punto correspondiente al centro de rotación articular:

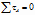
    Modelación: Se presenta el siguiente modelo vectorial para una flexión de codo en una situación en la cual el antebrazo está supinado (Figura 0):

    El agonista o motor principal de la flexión de codo con antebrazo supinado es el músculo bíceps braquial, el cual posee dos porciones. La porción corta se origina en la apófisis coracoides de la escápula y, la porción larga se origina en la tuberosidad supraglenoidea del mismo hueso. Ambas convergen distalmente para insertarse en la tuberosidad bicipital del radio y en la aponeurosis del antebrazo por la expansión aponeurótica del bíceps.

    Todo el segmento anatómico antebrazo-muñeca-mano más la carga sostenida, puede considerarse como un cuerpo rígido en equilibrio bajo la acción de varias fuerzas.

    La fuerza muscular Fm realizada por el bíceps braquial actúa sobre el punto de inserción de dicho músculo en el hueso radio, llamado tuberosidad radial y ubicado a una distancia a de la articulación del codo. La línea de acción de Fm forma un ángulo con el eje X (o con el eje mecánico del antebrazo), este es el ángulo de tensión muscular que representa la dirección de Fm en el sistema cartesiano elegido.

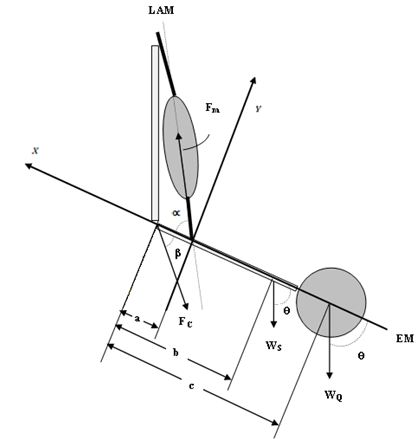
Figura 10. Modelo vectorial de la flexión de codo

    Otras fuerzas que actúan en el sistema son las de atracción que ejerce la Tierra hacia su centro, las cuales son fuerzas a distancia. Según Viladot (2001), de acuerdo a la tercera ley de Newton, “la reacción del peso, es decir, la fuerza que realiza el cuerpo sobre la Tierra, está evidentemente aplicada en la Tierra”. Así, los diferentes segmentos anatómicos del cuerpo humano, son atraídos hacia el centro de la tierra por fuerzas que son precisamente los pesos segmentarios, representados por vectores que se aplican en sus correspondientes centros de gravedad.

    El peso Ws del segmento anatómico actúa en el centro de gravedad Cg o baricentro del segmento ubicado a una distancia b de la articulación del codo. En general para un adulto promedio, este punto está ubicado en la unión de los dos tercios proximales con el tercio distal del antebrazo.

    El peso WQ de la carga actúa a una distancia de la articulación del codo.

    Ambos pesos WS y WQ actúan verticalmente formando un ángulo con el eje mecánico de la palanca anatómica del antebrazo.

    Durante la flexión de codo se producen fuerzas de reacción articular, ya que el cúbito se traslada posteriormente a medida que se produce el contacto con la apófisis coronoides (Nordin y Frankel, 2001). Estas fuerzas con o sin un objeto en la mano, se pueden calcular por medio de la técnica simplificada del cuerpo libre que aquí se analiza para fuerzas coplanares. Nicol et al. (1977), por medio de análisis biomecánico tridimensional, demostraron que la fuerza de reacción generada en el codo puede llegar a ser igual hasta tres veces el peso corporal, es decir, hasta 180 kp para una persona que pesa 60 kg.

    La fuerza de contacto FC es una reacción del húmero sobre los huesos del antebrazo, aplicada en la articulación formando un ángulo con el eje mecánico del antebrazo y es necesaria para garantizar el equilibrio en una posición determinada.

    Condiciones de equilibrio: 

    La primera ecuación representa un equilibrio de traslación en el plano sagital para los movimientos de flexo-extensión del codo y se puede expresar respecto a los dos ejes de la siguiente manera: , 

ecuaciones que incluyen respectivamente los componentes rectangulares de las fuerzas que son paralelos y perpendiculares al eje mecánico del antebrazo.

    La segunda ecuación representa un equilibrio de rotación respecto a la articulación y más específicamente respecto a un punto llamado centro instantáneo de rotación del codo.

    Desarrollando la parte operacional matemática de tales ecuaciones:

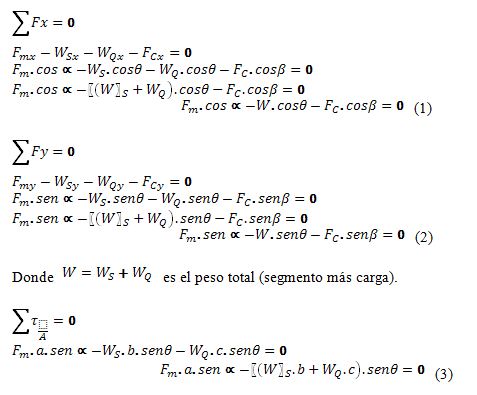
    Despejando en la ecuación (3) se obtiene una fórmula general para calcular el valor de la fuerza muscular en cualquier posición haciendo los ajustes necesarios de los parámetros que intervienen en el problema:

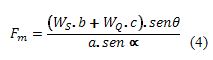
    Como cuando varía en el rango , entonces en ese rango y, teniendo en cuenta que es mucho menor que y que , el numerador de la expresión (4) es mucho mayor que su denominador, lo que significa que la fuerza muscular aplicada es mucho mayor que la carga sostenida incluyendo el peso del segmento anatómico.

    Si se realiza una pequeña flexión de hombro aumentando el ángulo del eje mecánico del brazo respecto a la vertical, pero sin rotar el segmento anatómico antebrazo-muñeca-mano, solo trasladándolo, ocurre que el ángulo de tensión muscular disminuye y el músculo bíceps braquial ha de ejercer una fuerza Fm mayor para compensar la disminución de la función trigonométrica .

    Experimentalmente se sabe que en el gesto analizado, la Fm del bíceps alcanza un valor 6 a 8 veces mayor que la carga que se levanta, la cual incluye el peso del segmento y la resistencia externa adicional. El ser desfavorable a la aplicación de la fuerza pero favorable a la producción de movimiento es característico de este tipo de palanca, que como las de tercer género abundan en las acciones locomotoras del cuerpo humano (Fucci et al., 1998).

    Si en el sistema de ecuaciones (1), (2), (3) expresadas en las condiciones de equilibrio, conocemos los valores de la fuerza Fm, los pesos WS y WC, el ángulo y las distancias y , podemos calcular el valor y la dirección de la reacción articular Fc.

    Reescribiendo las ecuaciones (1),(2),(3) respectivamente, como sigue:

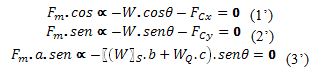
    Al despejar respectivamente FCx, FCy y de las ecuaciones (1’),(2’),(3’) obtenemos:

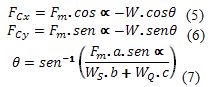
    Sustituyendo (7) en (5) y (6) obtenemos:

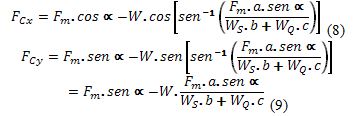
    Luego se calcula el módulo de Fc aplicando el Teorema de Pitágoras:

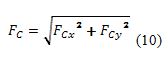
    Y su dirección se encuentra por medio de la expresión:

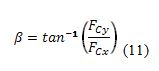
    Aplicación 1: Utilizando métodos radiológicos se ha evidenciado que la línea de acción muscular del bíceps braquial forma un ángulo de 15º con el eje mecánico del brazo (Serway, 1997) cuando el ángulo articular del codo es 90º, situación en la que los ejes mecánicos de brazo y antebrazo son perpendiculares (Figura 11). Así, la fuerza muscular es oblicua y posee dos componentes rectangulares. Entonces, en una situación estática de equilibrio, la fuerza de contacto debida a la reacción de húmero sobre el antebrazo, también debe ser oblicua de tal forma que posea un componente FCx paralelo al eje mecánico del antebrazo que equilibre el componente Fmx de la fuerza muscular, también paralelo al eje mecánico del antebrazo.

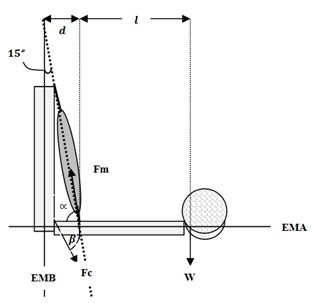
Figura 11. Análisis vectorial de la flexión de codo para un ángulo articular de 90º

    En estas condiciones el ángulo de tensión muscular es (la suma de los ángulos internos de un triángulo es 180°). Al asumir por ejemplo que el peso total W del segmento más la carga es 50 N y se aplica a una distancia del codo, y además, la fuerza del bíceps se aplica en la tuberosidad radial a una distancia del codo, entonces puede calcularse completamente las fuerzas Fm y Fc.

    Ajustando los datos de este problema a la ecuación (4) del modelo:

    Ahora tenemos en cuenta la ecuación (9) del modelo para calcular :

    Ahora se calcula la dirección de con la ecuación (11):

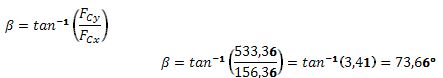
    con el eje mecánico del antebrazo.

    Aplicación 2: Cuando la disposición de los segmentos anatómicos del brazo y del antebrazo es tal que el hueso húmero está ligeramente inclinado hacia delante y la línea de acción muscular del bíceps braquial es perpendicular al eje mecánico del antebrazo, el ángulo de tensión muscular vale 90º (Figura 12).

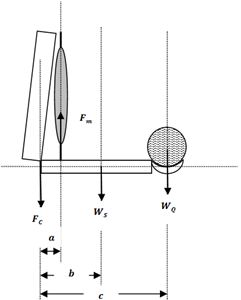
Figura 12. Análisis vectorial de la flexión de codo para un ángulo de tensión muscular de 90º

    Observamos qua las fuerzas son perpendiculares al eje mecánico del antebrazo, por tanto la fuerza de contacto debida a la reacción del húmero sobre el antebrazo, también debe ser perpendicular en condiciones de equilibrio.

    Si se conocen los valores , se pretende calcular el valor de .

Condición de equilibrio rotacional:

Observación: El resultado del cociente 

 

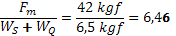
resulta coherente con la situación conocida de que en el gesto de flexión de codo estudiada, el músculo bíceps braquial debe realizar una fuerza 6 a 8 veces la carga levantada (peso del segmento más resistencia externa), pero esto se compensa por el importante desplazamiento de la carga frente al pequeño desplazamiento del músculo generado por su contracción muscular.

    En este ejercicio de aplicación se pudo haber utilizado directamente las ecuaciones (4) y (9) del modelo:

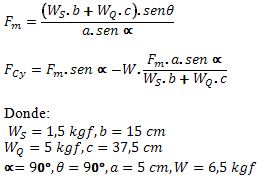
    Nótese que como todas las fuerzas son perpendiculares al eje mecánico del antebrazo, el valor de viene dado por .

    La discusión de este problema permite comprender el porqué de las inmovilizaciones del miembro superior con cabestrillo en esta posición. Para un ángulo de tensión muscular de 90° se minimiza el componente paralelo al eje mecánico de la palanca, atenuando las fricciones articulares, ayudando a disminuir la inflamación y favoreciendo la consolidación de una eventual fractura.

Conclusiones

    La modelación físico-matemática es una herramienta muy útil para el análisis del gesto articular. El uso de algoritmos, ecuaciones y propiedades elementales de las ciencias exactas aplicadas en contexto ayudan a la interpretación de los fenómenos del movimiento humano. Se hizo un tratamiento sistemático para el gesto de flexión de la articulación del codo, pero puede hacerse una verificación para los demás movimientos de esta articulación (extensión, pronación, supinación) y de manera general para las demás articulaciones diartrósicas del cuerpo humano.

    La distancia entre las ciencias exactas y las ciencias humanas se reduce vertiginosamente y, el análisis vectorial es uno de sus principales hilos conductores.

Bibliografía

• Boone DC, Azen SP. Normal range of motion of joints in male subjects. J Bone Joint Surg, 1979; 61A: 756-759.

• Calais-Germain, Blandine. Anatomía para el movimiento. Tomo I. 2ª ed. La liebre de Marzo: Barcelona. 2004.

• Cromer, Alan H. Física para las ciencias de la vida. 2ª ed. Reverté, S.A. Barcelona. 1992.

• Draque, Richard; Vogl, Wayne; Mitchell, Adam. Anatomía para estudiantes. 1ª ed. Elsevier: Madrid. 2007.

• Fucci, Sergio; Benigni, Mario y Vittorio Fornasari. Biomecánica del aparato locomotor aplicada al acondicionamiento muscular. 3ª ed. Harcourt Brace: Madrid. 1998.

• Gardner, Ernest; Gray, Donald; O’Rahilly, Ronan. Anatomía. 2ª ed. Salvat Editores, S.A. Barcelona. 1971.

• González Ibeas, J. Introducción a la Física y Biofísica. Alhambra: Madrid. 1974.

• Gowitzke, Barbara A. El cuerpo y sus movimientos, bases científicas. 1ª ed. Paidotribo: Barcelona. 1999.

• Guillén del Castillo, M. y Linares Girela, D. Bases biológicas y fisiológicas del movimiento humano. Médica Panamericana, S.A. Madrid. 2002.

• Gutiérrez Dávila, Marcos. Biomecánica deportiva. 1ª reimpresión. Síntesis: Madrid. 1999.

• Hernández Corvo, Roberto. Enciclopedia general del ejercicio. Tomo III: El sistema locomotor. Paidotribo, S.A. Barcelona. 1990.

• Herrera, Miguel Ángel. Biofísica, Geofísica, Astrofísica. Para que sirve la Física. Ediciones Científicas Universitarias: México. 2001.

• Hislop J., Helen y Montgomery, Jacqueline. Pruebas funcionales musculares. Daniels – Worthingham’s. 6ª ed. Marban: Madrid. 2002.

• Izquierdo, Mikel. Biomecánica y bases neuromusculares de la actividad física y el deporte. Médica Panamericana S.A. Madrid. 2008.

• Luttgens, Kathryn y Wells, Katharine. Kinesiología. Bases científicas del movimiento humano. 7ª ed. Saunders College Publishing. Pila Teleña: Madrid. 1982.

• Miralles Marrero, Rodrigo. Biomecánica clínica del aparato locomotor. 1ª ed. 2ª reimpresión. Masson: Barcelona. 2002.

• Molano Tobar, Nancy. Manual de examen muscular y valoración de la movilidad articular. Kinesis: Armenia. 2008.

• Nicol, A.C., Berme, N. y Paul J.P. (1977). A biomechanical analysis of elbow joint function. In Joint Replacement in the Upper Limb (pp. 45-51). London: Institution of mechanical Engineers.

• Petherick M, Rheault W, Kimble S, Lechnerc C, Senear V. Concurrent validity and intertester reliability of universal and fluid-based goniometers for active elbow range of motion. Phys Ther 1988; 68: 966-969.

• Pineda, Fabio. Kinesiología. Publicaciones Politécnico Colombiano “Jaime Isaza Cadavid”: Medellín. 1997.

• Robertson, Gordon; Caldwell, Graham; Hamill, Joseph; Kamen, Gary y Saunders Whittlesey. Research methods in Biomechanics. Human Kinetics: Champaign (United States). 2004.

• Serway, Raymond. Física. Tomo I. 4a ed. McGraw Hill Interamericana: México. 1996.

• Viladot Voegeli, Antonio. Lecciones básicas de biomecánica del aparato locomotor. Springer: Barcelona. 2001.

• Zill, Dennis y Dewar, Jacqueline. Álgebra y trigonometría. 2a ed. McGraw Hill Interamericana S.A. Bogotá. 1999.

Otros artículos sobre Biomecánica

	Búsqueda personalizada
EFDeportes.com, Revista Digital · Año 17 · N° 171 | Buenos Aires, Agosto de 2012   © 1997-2012 Derechos reservados