Nuevo modelo mecánico del músculo
	*Profesor/a de Biomecánica Deportiva Facultad de Cultura Física de Pinar del Río **Especialista de I Grado en Medicina Deportiva Centro Provincial de Medicina Deportiva de Pinar del Río **Especialista de II Grado en Neurofisiología Centro Nacional de Neurología y Neurocirugía (Cuba)	Omar Iglesias Pérez* Zelma Quetglas González* Razel Martínez Quetglas** Isvan Álvarez Herrera*** zelmaqg@inder.cu
	Resumen           Actualmente el conocimiento de la composición muscular y su relación con el aparato contráctil ha tomado hoy día una primordial importancia para entender los mecanismos de elasticidad y su influencia en la fuerza muscular. Los modelos mecánicos del músculo no tienen en cuenta las características viscoelásticas del mismo, que toman fundamental importancia en el momento de absorber eficientemente los movimientos, y la disipación de energía mecánica cuando termina la contracción muscular, además la imposibilidad de los modelos existente de explicar diferentes hechos experimentales ha puesto en crisis los modelos mecánicos actuales. La imposibilidad de explicar los diferentes valores de la capacidad elástica reactiva durante un salto en profundidad y los diferentes valores de la elasticidad hace necesario la proposición de otro modelo mecánico del músculo, que tengan en cuenta sus características viscoelásticas y pueda explicar de una forma coherente las evidencias experimentales.           Palabras clave: Modelos mecánicos. Contracción muscular. Biomecánica. Ecuación de la contracción muscular. Componente viscoelástico.
	EFDeportes.com, Revista Digital. Buenos Aires - Año 17 - Nº 170 - Julio de 2012. http://www.efdeportes.com/

1 / 1

Introducción

    El músculo consta de un componente activo contráctil y de un componente pasivo no contráctil. El primero consiste en un sistema de fibras entrelazadas cuyo propósito se basa en movilizar unas en relación con las otras y producir una contracción global. El segundo comprende una serie de diferentes tipos de tejido conectivo como los tendones, ligamentos y vainas alrededor de las fibras musculares. Estos proporcionan un marco de referencia estructural para los músculos y una red de conexiones entre las partes del sistema musculoesquelético, que estabilizan y transmiten las fuerzas por todo el cuerpo. Funcionalmente, tienen un papel importante en la absorción y liberación de la energía elástica para mejorar la eficacia de la acción muscular.

Un modelo muscular simplificado

    Los modernos avances en el entrenamiento hacen necesario modificar el modelo muscular de Hill (1938) (figura 1). Resulta demasiado simplista referirse al complejo muscular incluyendo solamente los elementos contráctil y elástico, ya que sus componentes muestran otras propiedades mecánicas como el frenado y la deformación. El hecho que varios componentes incluyendo el tejido conectivo y los líquidos intersticiales, del complejo muscular sean viscoelásticos sugiere inmediatamente que el frenado debe ser importante en el moldeado de cualquier músculo.

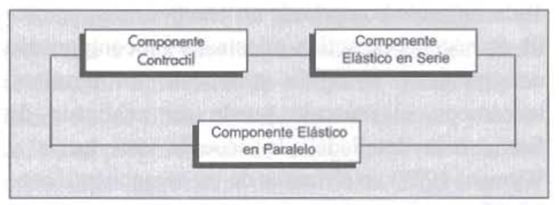
Figura 1. Modelo Mecánico de Hill

    Por ejemplo un análisis con plataforma de fuerza reveló que las vibraciones del complejo muscular se disipan en forma de un movimiento decreciente armónico simple, lo cual indica que el componente elástico en serie (CES) y el componente elástico en paralelo (CEP) están asociados con unos mecanismo de frenado eficientes que absorben la energía y suavizan los movimientos, protegiendo, por tanto, de lesiones relacionadas con cargas resonantes a determinados niveles. Además, el tejido conectivo dentro del complejo muscular tiene una razón específica de frenado y un valor determinado de rigidez mecánica que es diferente en sujetos de diferente sexo, estado de lesión e historial deportivo.

    Por otra parte, la rigidez mecánica tiende a disminuir o a permanecer aproximadamente constante después del ejercicio, mientras que la razón de frenado aumenta siempre después del ejercicio lento, sostenido o explosivo en hombres y mujeres. Este cambio tiene lugar posiblemente para lograr que los potenciales peligros de la fatiga muscular local o neuromuscular estén compensados por un frenado satisfactorio a través de tensiones subsiguientes. La relación de frenado y de rigidez tienden ambas a aumentar en los sujetos cargados con una masa adicional, de nuevo una respuesta adaptativa que tiende a mantener la estabilidad bajo un amplio abanico de condiciones del ejercicio. La razón de frenado tiende a aumentar con la masa corporal y a ser más elevada en las mujeres. Todo lo anteriormente propuesto sirvió de base para la construcción de un modelo mecánico del músculo propuesto por Levin-Wyman y modificado posteriormente por Verjoschanky (2004) (figura 2) donde no solo tiene los elementos elásticos en serie y paralelo , sino también un elemento de frenado y un elemento deslizante con la opción de poder explicar las evidencias experimentales anteriormente expuestas.

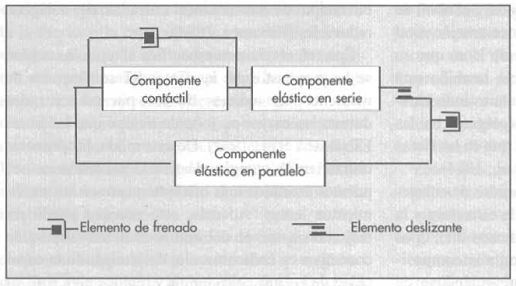
Figura 2. Modelo mecánico de Levin-Wyman modificado por Verjoschansky

    Un trabajo similar realizado por Greene y McMahon sobre sujetos que saltaban con diferentes grados de flexión de la rodilla en una tabla flexible a diferentes frecuencia reveló que la rigidez mecánica del tejido blando esta determinada por el ángulo articular.

    Es importante destacar que la vida de los puentes cruzados entre los filamentos de actina y miosina es limitada, variando de 15 a 120 milisegundos. Por lo tanto, la utilización de la energía elástica almacenada, es vital que el periodo de estiramiento y el periodo de transición entre el estiramiento y el subsiguiente acortamiento sean cortos. Un estiramiento largo simplemente provoca un deslizamiento entre los componentes del complejo muscular, desperdiciándose el potencial elástico de los puentes cruzados. Sin embargo, un tiempo de emparejamiento corto provocado por un pre-estiramiento de poca amplitud evitara la rotura de los puentes cruzados y facilitara el mejor uso de la energía elástica almacenada durante la fase de acortamiento, que es de particular importancia en actividades como el salto, la halterofilia y la pliometría.

    Parece también que las fibras de contracción lenta (ST) y la de contracción rápida (FT) tienen diferentes propiedades viscoelásticas, que le permiten hacer uso diferente del ciclo estiramiento-acortamiento. Por ejemplo, los test de salto vertical muestran que una ejecución rápida, con una fase de estiramiento de poca amplitud, optimiza el rendimiento de los músculos vastos medios, que son ricos en fibras FT. Los músculos extensores de la rodilla en los sujetos con una mayor proporción de fibras ST obtuvieron mejores resultados en saltos lentos, con una mayor amplitud y con un periodo de transición entre el estiramiento y el acortamiento más largo. Bosco y otros (1982) consideran que esta diferencia es una consecuencia de las distintas vidas de los puentes cruzados entre las fibras FT y las ST.

    Esta investigación sugiere que el modelo de Levin-Wyman debe modificarse para incluir elementos de frenado no lineales (ya que los componentes musculares se mueven en un fluido) y un elemento deslizante (elemento este que permite la no espiralización del tejido conectivo en reposo cuando la tensión alcanza valores críticos en el sistema.

    Además, la variación del nivel de rigidez en relación con el ángulo articular demuestra que las características mecánicas del CES y del CEP no son lineales. En otras palabras, estos no obedecen simplemente a la ley de Hooke. El elemento de frenado no ha sido asociado al CEP, ya que existe un movimiento mínimo entre estructuras como el sarcolema y las vainas alrededor de las fibras musculares que se considera que comprenden al CEP.

    Los modelos musculares presentados destacan que el entrenamiento de la condición física no solo debería centrarse en el desarrollo muscular, sino también en el acondicionamiento de todos los tejidos conectivos asociados con la estabilidad y la movilidad. Recientes descubrimientos confirman este hecho cuando establecen que un aumento de la fuerza puede no estar únicamente relacionado con un incremento de la densidad de los elementos proteicos contráctiles del músculo, sino también con una mejora de la transmisión de la fuerza de las fibras musculares al sistema esquelético. A este respecto un aumento de la fuerza del tejido conectivo y una mejor rigidez del complejo muscular pueden disminuir la disipación de al fuerza generada por los sarcómeros individuales y los tejidos vecinos. La investigación en este aspecto fue instigada para explicar porque la fuerza muscular puede aumentar sin aumento del tamaño muscular o de la densidad de los filamentos musculares.

    La hipertrofia producida por el acondicionamiento de la fuerza y por la mejora de la eficacia neuromuscular a través de un adecuado entrenamiento de velocidad-fuerza y por impulsión puede también afectar el almacenamiento y la utilización de energía elástica. Puesto que la hipertrofia se asocia con un aumento de la cantidad y la fuerza del tejido conectivo, así como con un incremento del número de puentes cruzados, el potencial para el almacenamiento de la energía elástica también aumenta, especialmente si el entrenamiento incluye una adecuada estimulación neuromuscular. Este hecho puede ser de gran importancia para mejorar el rendimiento en deportes de potencia acíclicos como la halterofilia, los saltos y lanzamientos en el atletismo, así como en especialidades de resistencia cíclicas como las carreras de fondo y el ciclismo.

    Con todo lo anteriormente descrito nos podemos percatar que los modelos existentes no recogen las características viscoelásticas del músculo mecanismo muy importante a la hora de explicar cómo se disipa la energía en la contracción muscular, también poseen la imposibilidad de explicar los diferentes valores de la capacidad elástica reactiva manifestada en saltos en profundidad en dependencia del tiempo de contacto. Los modelos existentes no explican la forma de la curva de fuerza velocidad de inclinación de la rodilla reportado por Bosco[], debido a todo lo anteriormente expuesto nos propusimos en proponer un modelo mecánico del músculo que a su vez se apoyara en un modelo matemático, con la idea de darle respuesta a todas las incongruencias anteriormente explicadas, este posee un elemento elástico en serie, un elemento elástico en paralelo, el elemento contráctil está separado para las fibras de contracción lenta y las fibras de contracción rápidas, así como un elemento viscoelástico para cada tipo de fibra debido a las diferencias que existe entre las fibras de contracción rápida y las fibras de contracción lenta, de esta forma se le da respuesta a muchas de las incongruencias anteriormente planteadas (ver figura 3).

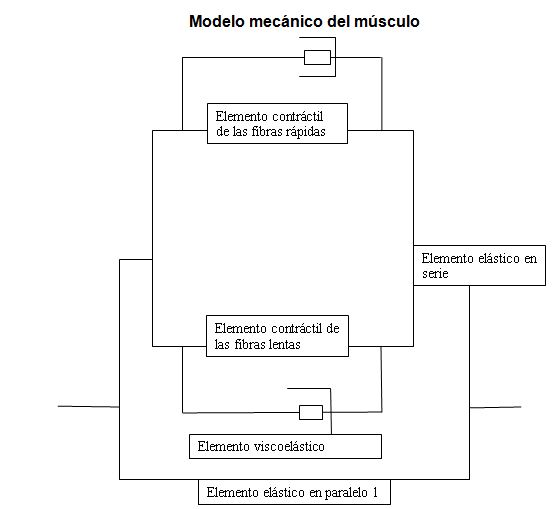
Figura 3. Modelo mecánico del músculo

    La ecuación diferencial que caracteriza el movimiento en el músculo, tienen las siguientes formas, teniendo en cuenta el carácter viscoelástico del músculo.

    La forma corriente de la solución complementaria es:

    Este es un movimiento sobreamortiguado, debido a las características del músculo, y a la rapidez de la pérdida de la energía potencial elástica almacenada en los componentes elásticos, tanto en serie como en paralelo, se puede deducir que este es un sistema sobre amortiguado.

    Un término que surge debido al sistema es la energía de disipación cuya expresión matemática es:

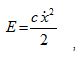
    este término está ligado fuertemente con la capacidad elástica almacenada en el músculo en los gestos explosivos.

    Si se tiene en cuenta que Hill llego a la ecuación fundamental de la contracción muscular mediante consideraciones energéticas sin tener presente las características viscoelásticas propiamente del músculo.

    De la ecuación de movimiento se tiene:

    De las características del modelo biomecánico planteado se obtiene

    Donde Q es la cantidad de calor y P el peso

    Si se gráfica las variaciones de Q en el tiempo, presenta un comportamiento lineal, esto está en similitud a todo lo planteado por Hill, de aquí que derivando dicha ecuación en el tiempo se llega a:

    Como puede verse esta es la ecuación fundamental de la contracción muscular teniendo en cuenta las características viscoelásticas del músculo

Donde v es la velocidad de contracción del músculo

    Si en la ecuación propuesta se elimina el término viscoelástico llegamos a la ecuación de Hill.

Conclusiones

1. En el siguiente trabajo se propuso un nuevo modelo mecánico del músculo donde se tiene en cuenta las características viscoelásticas del músculo, tanto en su forma estructural como en su parte matemática.

2. La solución del régimen subamortiguado explica la forma en que se disipa la energía después que desaparece la contracción muscular, y el termino de cómo se disipa la energía dependiendo de los valores de la constante viscoelástica.

3. Se obtuvo la ecuación fundamental de la ecuación la contracción muscular teniendo en cuenta las características viscoelásticas del músculo, la cual si se hace cero la constante viscoelásticas se reduce a la ecuación de Hill.

Bibliografía

• Bosco, C. y col. (1982). Combined effect of elastic energy and mioelectrical potentaiation during streth-shortening cycle exercise. Acta Physiol Scand 114, 557- 565.

• Bosco, C., Cardinale, M., y Tsarpela, O. (1999). Influence of vibration on mechanical power and electromyogram activity in human arm flexor muscles. European Journal of Applied Physiology 79, 306 – 311.

• Bosco, C., Tarkka, I., y Komi P. (1982). The effect of elastic energy and mioelectrical potentiation triceps surae during strech-shortening cycle exercise. Int J Sports Med 3, 137-140.

• Bosco, C., Tihanyi, J., Komi, P., Fekete, G., y Apor, P. (1982). Store and recoil of elastic energy in slow and fast types of human skeletal muscles. Acta Physiol Scand 116, 343 – 349.

• Coyle EF, Costill DL, Lesmes GR. Leg extension power and muscle fiber composition. Med Sci Sport 11:12-15, 1979.

• Cronin, J.B., y MacNair, P.J. (2000). The role of maximal strenght and load on initial power production. Medicine and Science in Sport and Exercise 3, 1763 – 1769.

• Herzog, W. (1997). What is the series elastic component in skeletal muscle? J. Appl. Biomechanics 13 (4), 443 – 448.

• Hill, A.V. (1938). The heat of shortening and the dynamic constants of muscle.

• Hochmuth, G. (1973). Biomecánica de los movimientos deportivos. Madrid, España: Ed. Doncel.

• Huxley HE. The mechanism of muscular contraction. Science 164(3886): 1356-1366, 1969.

• Información general y documentos Universidad de León. (2007). Pruebas. Fuerza explosiva del tren superior. Obtenido el 6 de Noviembre del 2009 de http://www.fcafd.unileon.es/pruebas.htm

• Komi, P. (1973). (1984). Physiological and biomechanical correlates of muscle function. Exerc and Sports Sciences 14, 81 – 121.

• Komi, P., y Buskirk, E. (1970). Effect of eccentric and concentric muscle conditioning on tension and electrical activity of human muscle. Ergonomics 15, 417-434.

• Komi, P., y Hakkinen, K. (1986). Training – induced changes in neuromuscular performance under voluntary and reflex conditions. Eur. J. Appl. Physiol. Occup. Physiol. 55 (2), 147 – 155.

• Verkhoshansky, Y. (2004) La fuerza explosiva y el ciclo excéntrico-concéntrico. Ed. Paidotribo, Barcelona.

Otros artículos sobre Actividad Física y Salud

	Búsqueda personalizada
EFDeportes.com, Revista Digital · Año 17 · N° 170 | Buenos Aires, Julio de 2012   © 1997-2012 Derechos reservados