Introducción
Las tendencias actuales en la enseñanza de la Matemática abogan por la
utilización de los ejercicios vinculados a la práctica, como vía para
adquirir sólidos conocimientos, el desarrollo de las posibilidades
intelectuales y del pensamiento lógico. Los profesores tienen la obligación de
formar hombres preparados, con un alto nivel de conocimientos; pero también
preparados para la vida, con una interpretación interdisciplinaria de los
procesos y los fenómenos. También tiene como misión investigar cómo mejorar
la enseñanza de la disciplina, y tener presente al estudiante, desde distintos
puntos de vista, siempre con la claridad de que en él, debe estar el proceso de
enseñanza aprendizaje, es decir, saber si aprende determinados contenidos,
cómo los aprende, cómo interioriza y aplica propiedades.
Relacionar los espacios deportivos con los contenidos geométricos constituye
una vía importante para la adquisición de conocimientos, hábitos y
habilidades para el desarrollo intelectual del futuro profesional de la Cultura
Física. No hay dudas de que esta forma de enseñar y aprender despierta mayor
interés cognoscitivo ya que el estudiante comprende su importancia y su
utilidad, y cómo pueden utilizarse de una manera concreta y específica los
conocimientos matemáticos adquiridos.
Existen diferentes criterios acerca de ¿qué enseñar en Geometría?, ¿cómo
enseñarla?, ¿a quiénes va dirigida?, ¿en qué orden se debe enseñar? Pero
lo que sí está claro es que la enseñanza es necesaria y de gran importancia
en todos los niveles de estudio, pues la Geometría es la rama que más
interviene en el aprendizaje de las demás ramas de la Matemática (Álgebra y
Análisis Matemático), debido a que aporta la "interpretación
geométrica" de muchos resultados, a través de la "representación
visual", que en la Geometría es una necesidad y en las demás partes de la
Matemática, una valiosa ayuda. Además, con esta disciplina se puede lograr,
entre otros aspectos, el desarrollo del pensamiento lógico de los estudiantes y
el desarrollo del pensamiento geométrico-espacial. (Flores, 1990)
Desde la Enseñaza Primaria, Secundaria Básica y Preuniversitaria se profundiza
sobre todos los contenidos geométricos, se estudian nuevas propiedades de los
polígonos, problemas prácticos de cálculo geométrico, elaboración de
esbozos de figuras planas a partir de un modelo; no obstante, es frecuente
encontrar en estas escuelas, estudiantes que no pueden resolver determinados
ejercicios, pues no tienen dominio de estas propiedades.
Con
estas deficiencias transitan por todas las enseñanzas y al llegar a la
universidad, no están suficientemente preparados para enfrentarse a situaciones
de la práctica, como es por ejemplo construir un campo para jugar Fútbol con
los requisitos técnicos específicos que debe cumplir. Jesús Ignacio Benítez
Llanes realizó una investigación acerca de los requerimientos a la hora de
construir un área deportiva y la importancia que tiene el conocimiento de las
mismas por todos los entrenadores, el mismo plantea: “...Se
debe garantizar que todo espacio donde se realice una actividad física
deportiva esté en perfecto estado y en óptimas condiciones, para que el
individuo pueda hacer gala de sus facultades atléticas sin preocuparse por las
lesiones. Para ello, todos los relacionados con la Cultura Física deben estar
bien preparados para dar respuesta a esta necesidad del hombre”.
Por lo que se puede apreciar en la Facultad de Cultura Física de Holguín es
que, de forma general los estudiantes no reciben conocimientos sobre ejercicios
geométricos relacionados con el deporte, que en la mayoría de los casos se
desconocen las posibilidades que brindan las disciplinas deportivas; los
problemas son tomados, en su mayoría, de libros de textos y folletos, algunos
elaborados por los docentes. Es evidente que existe un número elevado de
dificultades objetivas y subjetivas que influyen en el proceso enseñanza -
aprendizaje de la asignatura Matemática Básica.
Se considera que cuando el estudiante descubre la necesidad del conocimiento
matemático para la solución de problemas concretos del medio donde se
desenvuelve, el aprendizaje se hace más sólido y los conceptos, teoremas y
procedimientos que se necesitan retener se logran con mayor facilidad.
Los profesores que imparten la asignatura Matemática Básica en la Facultad de
Cultura Física “Manuel Fajardo” de Holguín, Cuba, le conceden gran
importancia a la realización de ejercicios geométricos para el desarrollo de
la independencia cognoscitiva en los estudiantes, no obstante, en la revisión
bibliográfica y observaciones que se han realizado, se pudo comprobar que
existen las siguientes insuficiencias:
-
Aún
se evidencian insuficiencias en la preparación científico-metodológica de
los docentes para el diseño de ejercicios geométricos contextualizados con
el deporte.
-
Los
métodos que se utilizan son reproductivos y no existe específicamente un
libro de texto para esta enseñanza.
-
Los
materiales elaborados por la universidad para la organización y desarrollo
del proceso de enseñanza- aprendizaje de la asignatura, no cuenta con
suficientes contenidos, que constituyan elementos de referencia para que el
profesor trabaje en este sentido.
-
Las
potencialidades que ofrecen los contenidos de la asignatura Matemática
Básica no se explotan para el logro de una perspectiva interdisciplinaria.
-
El
protagonismo de los estudiantes en las clases es de nivel bajo; la
motivación, en relación con la necesidad de consolidar e integrar lo que
han aprendido, de forma que se modifique su conducta es casi nula.
-
En
las clases prácticas prevalecen las actividades del nivel reproductivo.
Sin dejar de reconocer el extraordinario y brillante valor de las referencias
bibliográficas estudiadas, no se de forma general no se detectan propuestas
científicas que contribuyan a la solución de dicho problema; es importante
destacar además los trabajos que han constituido el principal soporte de la
tarea. (Álvarez, 2004; Cruz R, 2001; Cuenca, 2002; Torres, 1998; Velásquez,
2005; Cala, 2002; Fiallo, 2000; Labarrere, 1988; Llivina, 1999; Sigarreta, 2001;
Palacio, 2003; Campistrous y Riso, 1996)
También se puede constatar del análisis de la bibliografía especializada que
la problemática del vínculo del contenido de la enseñanza de la Geometría
con los espacios deportivos, mediante tareas docentes, no ha sido solucionada
satisfactoriamente; es decir la bibliografía que está al alcance no ha sido
confeccionada específicamente para este tipo de estudiantes; no se ofrece una
metodología a seguir, en torno a la vinculación del contenido de la enseñanza
de la geometría con el deporte.
Teniendo en cuenta el análisis realizado anteriormente se deriva el problema
científico: ¿Cómo favorecer la resolución de ejercicios geométricos a
través de tareas docentes de la asignatura Matemática Básica en los
estudiantes de primer año de la carrera de Cultura Física, de la Facultad de
Holguín, Cuba? En correspondencia con el problema planteado se propone como objetivo
de la investigación la elaboración de un sistema de
tareas docentes para favorecer el aprendizaje de los ejercicios geométricos
contextualizados con los espacios deportivos en los estudiantes del primer año
de la carrera de Cultura Física, de la Facultad de Holguín, Cuba.
Se emplearon métodos teóricos: el histórico-lógico, análisis-síntesis, la
inducción-deducción, la modelación; y empíricos como la observación,
entrevista, encuesta.
Desarrollo
La Geometría nació gracias a necesidades prácticas que tuvo el hombre al
enfrentarse a los problemas que la naturaleza y su quehacer diario le
impusieron, está considerada parte de la geometría euclidiana, pues ésta
estudia los elementos geométricos a partir de dos dimensiones. Tiene por objeto
estudiar la extensión, forma y posición de los cuerpos y de los elementos que
los constituyen. Esta rama de la Matemática tuvo su origen muchos siglos antes
de nuestra era, en Egipto, donde las periódicas inundaciones del Nilo hacían
desaparecer los límites o linderos de los terrenos, lo que obligó a aquel
pueblo a resolver problemas sobre fijar los límites de tierra. Los monumentos,
inscripciones y papiros revelan que, efectivamente, tenían bastantes
conocimientos prácticos de Geometría, los cuales aplicaban fundamentalmente al
objeto mencionado.
Son los griegos los que inician el estudio de la Geometría racional, como
ciencia pura, despejándola de su finalidad meramente práctica y utilitaria.
Tales de Mileto y Pitágoras de Samos, sabios griegos de la antigüedad, bien
pueden llamarse los padres de la Geometría.
Los problemas de construcción han sido siempre un aspecto interesante de la
Geometría, mediante la realización de construcciones geométricas, se puede
contribuir, de modo efectivo al cumplimiento de los objetivos de la enseñanza
de la Matemática.
La importancia de las construcciones geométricas se refleja en los programas de
Matemática desde los primeros grados en la escuela cubana. Así, al saber y
poder lograr con las construcciones geométricas, la realización de
construcciones mediante homotecias y movimientos del plano, y las construcciones
geométricas fundamentales: transportar segmentos y ángulos; trazar paralelas;
bisecar un segmento; bisecar un ángulo; trazar la perpendicular a una recta por
un punto dado de éste; trazar la perpendicular a una recta por un punto dado
exterior a ésta y trazar la perpendicular por el extremo de una semirrecta.
Así afirmar que as construcciones geométricas juegan un papel importante entre
los ejercicios de aplicación en la enseñanza de la Matemática. En el
tratamiento de contenidos geométricos, como por ejemplo: triángulos,
cuadriláteros, polígonos y circunferencia, los estudiantes aplican teoremas,
definiciones y las construcciones básicas ya conocidas; contribuyéndose a un
mejor figuración del saber y poder de los alumnos.
Con las construcciones, se hace un aporte también al desarrollo de una correcta
imaginación espacial, así como a la formación y desarrollo de habilidades en
los alumnos al realizar algunas construcciones determinadas, así se contribuye
al logro de los objetivos en el campo del desarrollo intelectual.
A los técnicos deportivos se les presenta sistemáticamente la necesidad de
construir las áreas deportivas, cumpliendo los requisitos técnicos
específicos de cada deporte, para impartir sus clases con la calidad requerida.
Para acometer esta tarea es necesario que, sepan aplicar los conocimientos
adquiridos en las clases de Matemática, relativos a las propiedades que cumplen
las figuras planas, la mayoría de los terrenos están trazados utilizando
figuras planas.
El contenido de la asignatura Matemática Básica que se introduce en el Plan de
Estudios “D”, en el primer año de la carrera de Cultura Física no es nuevo
para los estudiantes, por lo que él debe ser el protagonista principal en cada
actividad, de forma tal que se involucre activamente en la búsqueda de los
procedimientos de solución, en la discusión y el análisis de los resultados
encontrados. Por lo antes expuesto, el rol del profesor está llamado a crear
ejercicios geométricos para potenciar el pensamiento lógico, de modo tal que
se sienta la fuerte vinculación de la asignatura con las disciplinas deportivas
que recibe en el transcurso de sus estudios; para además resolver una de las
problemáticas del futuro egresado que es la falta de creatividad, aspecto
esencial en un investigador a este nivel para enfrentar los retos de la sociedad
del siglo XXI.
La Matemática, como asignatura, proporciona conocimientos a partir de
soluciones tomadas de la vida; necesidad imperiosa para desarrollar en los
alumnos el conocimiento de propiedades para utilizarlos en la práctica.
Al investigar acerca del desarrollo del pensamiento a través de la enseñanza
de diversas disciplinas, queda demostrado que se dedican en el mundo, equipos de
trabajo y el fin que se persigue es perfeccionar el proceso de enseñanza
aprendizaje para que los estudiantes obtengan los conocimientos esenciales,
desarrollen habilidades y capacidades para lograr el cambio de su medio social.
En este sentido, Glaser (1982) visualizó tres elementos de suma importancia
(también visto por Vigostky, 1985):
-
El estudiante como centro del proceso
-
La organización del conocimiento
-
La solución de problemas.
Dentro
de la misión como profesor, está: investigar cómo mejorar la enseñanza de la
disciplina, y tener presente al alumno, desde distintos puntos de vista, siempre
con la claridad de que en él debe estar el proceso de enseñanza aprendizaje,
es decir, saber si aprende determinados contenidos, cómo los aprende, cómo
interioriza y aplica propiedades.
A
los profesionales del deporte se les presenta sistemáticamente la necesidad de
construir las áreas deportivas, cumpliendo los requisitos técnicos
específicos de cada deporte, para impartir sus clases con la calidad requerida.
Para acometer esta tarea es necesario que, sepan aplicar los conocimientos
adquiridos en las clases de Matemática Básica, relativos a las propiedades que
cumplen las figuras planas, la mayoría de los terrenos están trazados
utilizando figuras planas. En su práctica deportiva, no todos los profesionales
cuentan con las instalaciones deportivas para impartir sus clases, viéndose en
la necesidad de construir áreas deportivas rústicas; teniendo en cuenta los
requisitos técnicos del deporte; al tener un buen dominio de las propiedades
que cumplen las figuras planas y su aplicación en la práctica se les facilita
ser creativos y objetivos a la hora de la construcción.
La
geometría plana es una parte de la geometría que trata aquellos elementos,
cuyos puntos están contenidos en un plano. Es importante que los estudiantes de
la Facultad dominen cada concepto, que interpreten cada propiedad o teorema, que
analicen las representaciones gráficas para que puedan aplicarlas con calidad a
su práctica profesional a la hora de construir un área de la actividad
física.
No
es primordial que un profesor de Cultura Física posea profundos conocimientos
sobre la construcción de los espacios para la actividad física deportiva, con
sus respectivas complejidades de estructuras y espacios que los conforman, o
esté calificado para distinguir los reglamentos de las federaciones de más de
100 deportes, lo que sí es importante es que el profesor de Cultura Física
domine las características de las instalaciones deportivas donde ejerce su
actividad.
Las
medidas para la proyección y construcción de los campos y áreas deportivas
son aspectos que deben formar parte del currículo docente de los profesores y
entrenadores. Las mismas deberán estar en correspondencia con los reglamentos
de cada deporte. El cumplimiento de los objetivos y tareas de la Educación
Física y los deportes depende de las medidas de los campos y áreas deportivas
existentes.
Con
el objetivo de ampliar los conocimientos de los profesionales de la Cultura
Física en relación a la construcción de los espacios para la actividad
física deportiva, se dan a conocer las medidas reglamentarias de un numeroso
grupo de instalaciones e implementos deportivos a partir de una revisión
actualizada, además de la inclusión de las relativas a otros deportes, cuyo
reglamento sólo aparece en manos de los comisionados o representantes a nivel
provincial.
Análisis
de los resultados de la aplicación
Con la
aplicación de la experiencia se desarrollaron habilidades en la resolución de
ejercicios geométricos a través de tareas docentes, en los estudiantes de
primer año en tres semestres, con un total de 25 brigadas donde se incluyeron
cursos para trabajadores y cursos regulares teniendo en cuenta los atletas,
donde se generalizó el trabajo de investigación, esto se evidencia mediante la
aplicación del diagnóstico inicial en cada semestre con un resultado general
de 19,48 % de aprobados y en el examen final del mismo un 89,77 % de promoción,
corroborando el planteamiento anterior en los estudiantes de primer año de la
carrera de Cultura Física en la asignatura Matemática Básica.
No
sólo el estudiante quedó en el saber hacer, sino crearon sus propios
ejercicios geométricos contextualizados con las áreas deportivas que hasta el
momento dominan dentro de su quehacer como futuros profesionales.
Se
creó como parte de la experiencia un Grupo Científico Estudiantil: “La
Matemática y el Béisbol” con los estudiantes escogidos para el
estudio. Se encuentra en fase final para publicar un material de apoyo a la
docencia. La experiencia constituye una de las exigencias del programa de
estudio de la asignatura objeto de investigación. La experiencia revolucionó
la forma de pensar y actuar de profesores y estudiantes.
A
continuación se proponen ejemplos de tareas docentes, donde se relacionan
ejercicios geométricos contextualizados con el deporte. Las tareas tienen una
estructura novedosa, se presentan tres situaciones docentes en cada tarea, la
primera para retroalimentar el contenido a tratar y dos situaciones relacionadas
con los espacios deportivos y situaciones similares objeto de estudio en las
esferas de actuación del profesional de Cultura Física.
Se
parte del objetivo general de la asignatura:
Poner
en práctica en la solución de situaciones y problemas propios de la
Matemática, en especial en sus aplicaciones a la Cultura Física, los métodos
y procedimientos propios del trabajo en la asignatura haciendo uso de los
significados asociados a su sistema de conocimientos, de manera consciente y con
una ética acorde con los valores que esta carrera aspira a desarrollar en sus
futuros egresados.
Tema:
Relaciones Geométricas
elementales
Objetivo
general
Activar
los conocimientos de conceptos y de relaciones geométricas en figuras planas
elementales, especialmente de igualdad y de semejanza entre sus elementos, y sus
aplicaciones al cálculo de áreas y perímetros de figuras planas y de volumen
y área lateral en las del espacio, así como aplicarlos en la solución de
problemas geométricos en general y en especial en su empleo en la cultura
física.
Objetivo:
Resolver ejercicios geométricos
aplicados a los espacios deportivos; a través de tareas docentes.
Ejemplo
de tarea docente:
-
Calcula el área y el perímetro de un cuadrado cuyo lado mide 15,0 dm.
-
La
instalación para la práctica del deporte Boxeo posee una zona de protección
de 8,0m de largo y 8,0m de ancho.
-
¿Cuántos metros de cuerda se necesitan para cercarla con cuatro vueltas?
-
Calcule la cantidad de lona que se necesitará para cubrir el cuadrilátero.
-
Si
se quiere cercar con alambre, el terreno que se utiliza para entrenar Hockey
cuya forma es rectangular, se sabe que mide 15 m de ancho y tiene un área de
300 m2. ¿Cuántos metros del material se necesitarán para cercar dicho
terreno?
Sugerencias
metodológicas
Interpretar
la aplicación de la geometría plana en la resolución de ejercicios
geométricos vinculados con espacios deportivos, para ello se debe hacer un
estudio de los conceptos y procedimientos que se relacionan a continuación:
Tema:
Aplicaciones de la trigonometría
Objetivo
general
Activar
los conocimientos y relaciones trigonométricas básicas y su aplicación en el
cálculo en el triángulo rectángulo y en la resolución de triángulos
cualesquiera así como en la demostración de identidades y en la
representación de las funciones trigonométricas fundamentales y en la
identificación de sus propiedades respectivas y de su posible utilización en
el campo de la cultura física.
Ejemplo
de tarea docente:
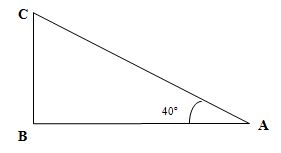
1.
Sea
ABC un triángulo rectángulo en B, si AC = 15 cm y α= 40o.
Calcula la longitud de los catetos AB y BC.
2.
Una escalera para entrenar en el tatami de Judo mide 6,5 m de largo y está
apoyada a una pared. Si el pie de la escalera está separada de la misma a 1,9
m. Halle el ángulo formado entre la escalera y la pared.
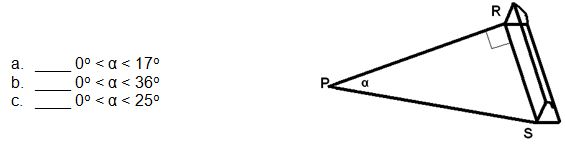
3.
Renay Malblanch, líder goleador del equipo Cuba sub-23 se encuentra en un punto
P del terreno a una distancia de 20 y 25 metros respectivamente de los extremos
R y S de la portería. ¿Qué valores de los que te relacionamos a continuación
puede tomar el ángulo de tiro α para que Renay anote un gol?
Sugerencias
metodológicas
Interpretar
la aplicación de la trigonometría en la resolución de ejercicios geométricos
vinculados con espacios deportivos, para ello se debe hacer un estudio de los
conceptos y procedimientos que se relacionan a continuación:
Conclusiones
Una vez culminado el proceso investigativo se arriban a las conclusiones
siguientes:
-
Aunque existen varios autores que tratan el tema de los ejercicios
geométricos a través de tareas docentes y dentro de ellos de los
contextualizados, hasta el momento no se ha encontrado un trabajo completo que
trate el tema de la contextualización con los espacios deportivos, hecho que
a través de los mismos se realizó el aporte de la investigación, por la
necesidad que presenta este tipo de estudiante de identificarse con la
asignatura Matemática Básica, o sea, qué utilidad le encuentran para su
futura profesión.
-
En el proceso enseñanza aprendizaje de la Matemática en el primer año de la
carrera de Cultura Física existen posibilidades reales para que los
estudiantes logren la vinculación del contenido de la enseñanza de la
asignatura con los diferentes espacios deportivos.
-
Además de un aprendizaje sólido de los contenidos matemáticos permitirá
cultivar una serie de valores y habilidades tales como:
-
Facilitar la comunicación a través de la resolución problemas
geométricos contextualizados con los diferentes espacios deportivos.
-
Aprender a estimar, calcular, proyectar y otras habilidades apoyadas
siempre en factores objetivos vinculados con el deporte.
-
Se desarrolla la laboriosidad, la responsabilidad, la perseverancia y el
amor al trabajo.
Bibliografía
-
ÁLVAREZ
DE ZAYAS, C. M. (1999). La escuela en la vida. Editorial Pueblo y Revolución.
Ciudad de La Habana. Cuba
-
ÁLVAREZ,
C (1996). Hacia una escuela de excelencia. Editorial Academia, Ciudad de La
Habana.
-
ANDREIEV,
I. (1984): Problemas Lógicos del Conocimiento Científico. Editorial Progreso,
Moscú.
-
ARTEAGA
VALDÉS, E. (2001). El sistema de tareas para el trabajo independiente creativo
de los alumnos en la enseñaza de la Matemática en el nivel Medio Superior.
Tesis en opción al título en Doctor en Ciencias Pedagógicas. Cienfuegos.
-
BENÍTEZ
LLANES, J. (2004). Espacios para la actividad Físico Deportiva. Editorial
Deporte. Ciudad Deportiva, Vía Blanca y Boyeros, Cerro, Ciudad de La Habana.
-
CAMPOS,
A. (1981): La Educación Geométrica. Universidad de Colombia, Vol. 1, Imprenta
Nacional, Bogotá.
-
CHÁVEZ,
J.A. DÍAZ PÉREZ, H. Cómo enseñar a confeccionar esquemas lógicos. Ed.
Pueblo y Educación, Ciudad de la Habana.
-
CONCEPCIÓN,
M.R. (1989). El sistema de tareas como medio para la formación y desarrollo de
los conceptos relacionados con las disoluciones en la Enseñanza General Media,
Tesis en opción al grado científico de Doctor en Ciencias Pedagógicas,
Holguín.
-
CORO
RODRÍGUEZ, F. (2005). Una propuesta metodológica para el tratamiento de la
Geometría Analítica en onceno grado. Trabajo de diploma, ISP “Enrique José
Varona”.
-
Diagnóstico
y caracterización. Consideraciones teóricas-metodológicas para su
realización. Departamento de Formación Pedagógica General, marzo 2001.
-
ESTRADA
DOALLO, M.R. (1997). Modelo didáctico dirigido a desarrollar el procedimiento
lógico de demostración.
-
FERIA
VELÁSQUEZ, F. (2002). Metodología para la formación de modos de actuación
del profesor de Matemática en la disciplina MEM. Tesis de Doctorado en Ciencias
Pedagógicas ISPH José de la Luz y Caballero, Holguín.
-
FERRÁS
FERRÁS, M. (2003). Una alternativa didáctica para el desarrollo de la
competencia en la traducción del lenguaje común al algebraico y viceversa, en
los alumnos de séptimo grado de la Secundaria Básica. Tesis en opción al
título de Master en Didáctica de la Matemática, Holguín.
-
GÁMEZ
GARCÍA, J.A. (1998). Una propuesta didáctica para incidir en el desarrollo de
la habilidad lógica “Deducción de propiedades” en la enseñanza de la
Matemática. Tesis en opción al título de Master en Didáctica de la
Matemática, Holguín.
-
GARCÉS
CECILIO, W. (2003). Desarrollo de modo de actuación para el trabajo con sistema
de tareas en la formación inicial del profesor de Matemática. Tesis Doctoral.
-
GARCIA,
M. (1989). Metodología para el logro de un aprendizaje significativo, pp.33-46.
Revista Tecnología y Comunicación Educativas, Nº 13, Julio, México, D.F.
-
La
interdisciplinariedad en la escuela: de la utopía a la realidad (2002) 16h.
Instituto Central de Ciencias Pedagógicas. Ciudad de La Habana, 2002. p9.
-
SUJOMLINSKI,
V. (1986) Entrego mi corazón a los niños. Editorial Progresó, Moscú.
-
TURNER,
L. y otros. (1988). Se aprende a aprender. Ed. Pueblo y Educación, Ciudad
Habana.
Otros artículos sobre
Educación Física
 |
|
|
EFDeportes.com, Revista Digital · Año 17 · N° 168 | Buenos Aires,
Mayo de 2012
© 1997-2012 Derechos reservados
|



