Fundamentos mecánicos del salto con pértiga


	Fundamentos mecánicos del salto con pértiga Pole vault mechanics
	Doctor en CC. de la Actividad Física y el Deporte Entrenador de club de atletismo. Nivel II *Doctor en CC. de la Actividad Física y el Deporte Universidad de Murcia. Entrenador nacional de atletismo. Nivel III (España)	Javier Bermejo Frutos* javier_bermejo_frutos@hotmail.com José Manuel Palao** palaojm@gmail.com
	Resumen En el presente trabajo se describen consideraciones técnicas de la prueba de salto con pértiga. Esta descripción se realiza desde el punto de vista de la biomecánica deportiva y se aborda tanto a nivel cualitativo como a nivel cuantitativo. El análisis de la mecánica del salto parte de una visión global de la prueba y de las características del implemento (la pértiga), hasta el establecimiento del modelo biomecánico de rendimiento, las diferentes divisiones temporales y mecánicas del movimiento, y los parámetros cinemáticos que más influencia tienen sobre el rendimiento del salto. Este trabajo busca incrementar la cantidad de información de la que disponen los entrenadores y atletas de la especialidad de salto con pértiga para así mejorar la evaluación de la técnica de la prueba y la mejora del rendimiento. Palabras clave: Salto con pértiga. Atletismo. Biomecánica. Técnica. Abstract This paper describes technical considerations of the pole vault. It is made from a sport biomechanics point of view, from both qualitative and quantitative perspectives. First of all, it gives an overview of the discipline and the characteristics of the implement (the pole). Next, it determines the biomechanical model of performance, it presents different time and mechanical divisions of the movement, and it discusses the kinematic parameters that influence jump performance the most. This document can help to increase the amount of information available to coaches and athletes specializing in pole vault in order to improve the technical evaluation of the discipline and performance improvement. Keywords: Pole vault. Track and field. Biomechanics. Technique
	EFDeportes.com, Revista Digital. Buenos Aires - Año 17 - Nº 168 - Mayo de 2012. http://www.efdeportes.com/

1 / 1

1.     Introducción

1.1.     Definición y objetivos

    El salto con pértiga es una prueba atlética de gran complejidad técnica (Gros y Terauds, 1983; Houvion, 1984; Russomanno, Rossetto, y Barros, 2009; Schiffer y Hommel, 1993; Wang, 2000) en la que un sistema biológico (el saltador) interactúa con un implemento de capacidades mecánicas elásticas (la pértiga) (Arampatzis, Schade, y Bruggmann, 2004; Ekevad y Lundberg, 1997; Frère, Chollet, y Tourny-Chollet, 2009; Hubbard, 1980; Linthorne, 2000; Schade, Arampatzis, y Bruggmann, 2000). El objetivo del saltador es superar un listón ubicado a una determinada altura, mediante la realización de una carrera de aproximación por una calle de 1.22 m de ancho, portando una pértiga, y utilizándola para batir apoyándola sobre un cajetín de 0.20 m de profundidad para proyectarse verticalmente tras la batida (Ruf, 2003).

1.2.     Consideraciones sobre la pértiga

    Debido a la interacción atleta-pértiga, el rendimiento de la prueba depende en gran medida de las características físicas del implemento y de sus propiedades mecánicas (Locatelli, 1987; Tenke, 1991; Tidow, 1989). En este sentido, el reglamento de la Asociación Internacional de Federaciones Atléticas (IAAF) especifica que la pértiga puede ser de cualquier material o combinación de materiales y que puede tener cualquier longitud y diámetro (IAAF, 2012). Esta reglamentación ha hecho que a lo largo de la historia se hayan buscado elementos materiales y longitudes que permitan la mejora del rendimiento.

    En relación a los materiales, estos han evolucionado desde las antiguas pértigas de madera hasta las actuales fabricadas en fibra de vidrio (Bosen, 1972), pasando por las pértigas de bambú y por las pértigas de aleación de duralumino. Las pértigas actuales no están construidas en fibra de vidrio en su totalidad, sino que la estructura de sus extremos está elaborada en fibra de carbono. Esto le otorga unas características de menor peso y mayor resistencia en las partes del agarre y apoyo en el cajetín y una mayor ligereza y flexibilidad en la parte central (Ruf, 1999). En relación a la longitud de la pértiga, es la evolución en los materiales lo que ha permitido incrementar su longitud (Carr, 1999).

    La introducción de las pértigas construidas en fibra de vidrio supuso una mejora anual en la marca de casi 4 cm, lo que anteriormente a su aparición sólo permitía progresiones de 1.63 cm de media (Anderson, 1997). Sin embargo, las superación de las marcas no se debe a que la pértiga proporcione mayor impulso, sino porque influye sobre la técnica (Bruggemann, Schade, y Arampatzis, 1999): a) aumentando la altura y anchura del agarre (Jagodin, 1973) y b) permitiendo un ángulo de batida menor (Frère et al., 2010). La mayor altura del agarre se relaciona con menor pérdida de energía durante la batida (Armbrust, 1993; Linthorne, 1994), mientras que la mayor anchura del agarre y el menor ángulo de batida se relacionan con una mejor conservación de la velocidad horizontal durante la batida y un mayor doblamiento de la pértiga, respectivamente.

    Son diversas las investigaciones que se han llevado a cabo teniendo como objetivo estudiar la contribución de la pértiga sobre el impulso final del atleta (Burgess, 1998; Dapena y Braff, 1993; Ekevand y Lundberg, 1997; Hubbard, 1980; Launder y Linthorne, 1990; Linthorne, 1994; Morlier y Mesnard, 2007). Las principales conclusiones de estos estudios son: a) que existe una longitud y dureza óptima en función de las características mecánicas de la técnica utilizada por cada saltador y b) que para conseguir el mayor aprovechamiento del impulso de la pértiga, las fases de clavada y despegue del pie de batida deben coincidir. Con esto se logra un mayor ángulo de la pértiga al contactar con el cajetín en la clavada, una mayor cantidad de velocidad horizontal del atleta, y permite utilizar pértigas más duras.

2.     Biomecánica del salto con pértiga

2.1.     Definición del modelo biomecánico

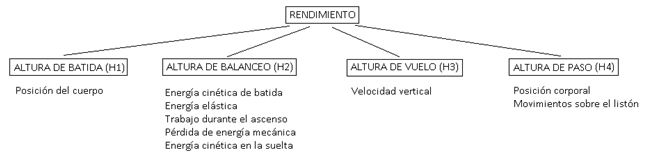
    El resultado del salto es la suma de diferentes alturas que componen el modelo mecánico del salto con pértiga (Hay, 1993): altura del centro de masas (CM) del saltador en el instante de la batida (H1), altura del CM cuando la pértiga está estirada (H2), altura del CM cuando el atleta suelta la pértiga (H3), y diferencia entre la máxima altura del CM y la altura en la suelta (H4). Las características morfológicas y la técnica determinan H1, la longitud de la pértiga y la capacidad para transferir la energía cinética determinan H2, la velocidad vertical en la suelta determina H3, y la técnica de paso determina H4 (figura 1). La contribución de las alturas sobre el rendimiento se fija en unos valores del 28-37% para H1, 63-72% para H2, y un 0% para H3 (Grabner, 1997; Liu, Li, y Wang, 2002). Algunos autores (Frère et al. 2010) critican este modelo porque limita el análisis de los parámetros cinemáticos.

Figura 1. Modelo biomecánico del salto con pértiga (Hay, 1993).

2.2.     División del gesto en fases

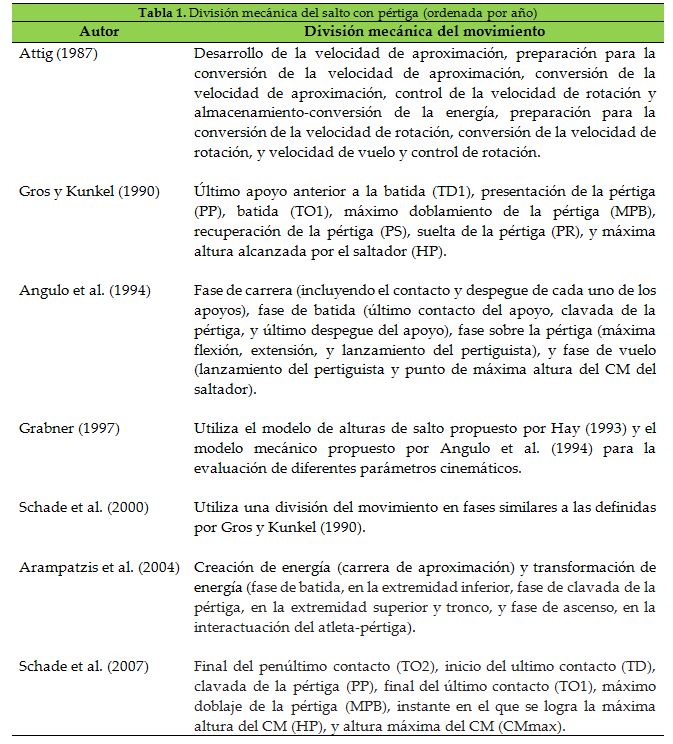
    En la bibliografía existen divisiones del gesto técnico en fases mecánicas (Attig, 1987; Angulo, Kinzler, Balius, Turro, Caubet, Escoda, y Prat, 1994; Arampatzis et al., 2004; Grabner, 1997; Gros y Kunkel, 1990; Schade et al., 2000; Schade, Isolehto, Arampatzis, Bruggmann, y Komi, 2007) y en fases temporales (Frère et al., 2010; Ruf, 1992; Schiffer y Hommel, 1993; Petrov, 2004; Sloan, 1993; Tidow, 1989; Jagodin, 1993). La división del movimiento en fases temporales es utilizada por los entrenadores para el análisis/evaluación de la técnica en términos cualitativos y para planificar el entrenamiento, mientras que la división del movimiento en fases mecánicas es utilizada por los investigadores para evaluar la interacción del sistema saltador-pértiga en términos cuantitativos (cinemática y cinética).

2.3.     Fases mecánicas del salto con pértiga

    Desde el punto de vista de la mecánica, durante un salto con pértiga se distinguen dos fases. En una primera fase, el deportista transfiriere energía cinética acumulada en la carrera de aproximación (velocidad horizontal) a la pértiga durante la batida. Esta energía se convierte en energía potencial de la pértiga durante el ascenso del saltador, mientras se produce el doblaje del implemento. En una segunda fase, el deportista recibe esta energía para superar el listón (Arampatzis, Schade, y Bruggemann, 2002).

    A diferencia de otras disciplinas de saltos, la transformación de velocidad de carrera a velocidad de batida se lleva a cabo con una mínima pérdida de energía (Linthorne, 2000), fijada en torno al 6-10% del total transferida (Schade, Arampatzis, y Bruggemann, 2006), o incluso con ganancias de energía (Arampatzis, Schade, y Bruggemann, 1997; Gros y Kunkel, 1993). Esta característica se debe a las propiedades elásticas de las pértigas (Ekevad y Lundberg, 1997). Por este motivo, para compensar esta pérdida el saltador debe maximizar la cantidad de energía cinética (velocidad de carrera) antes del momento de realizar la batida y desarrollar elevados nivel de fuerza en la musculatura de los hombros, los brazos, y el tronco (Frère et al., 2010).

    A continuación se exponen diferentes divisiones del gesto en fases mecánicas (tabla 1) y una representación gráfica (figura 2) del modelo técnico del salto.

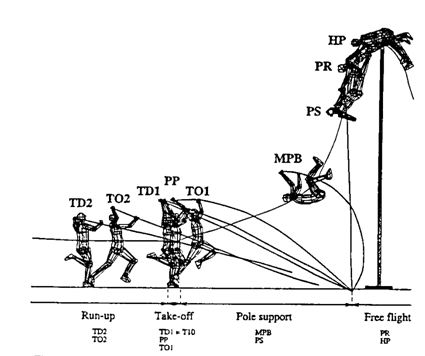
Figura 2. Fases del salto con pértiga y criterios de división de las fases en los estudios realizados a nivel biomecánico (Tomado sin modificaciones de Angulo el al., 1994).

Leyenda: TD2 = Penúltimo aterrizaje; TO2 = Penúltimo despegue; TD1 = Ultimo aterrizaje; PP = Presentación pértiga;

TO1 = Batida; MPB = Máxima doblaje pértiga; PS = Recuperación pértiga; PR = Suelta pértiga; HP = Pico de altura.

2.4.     Fases temporales del salto con pértiga

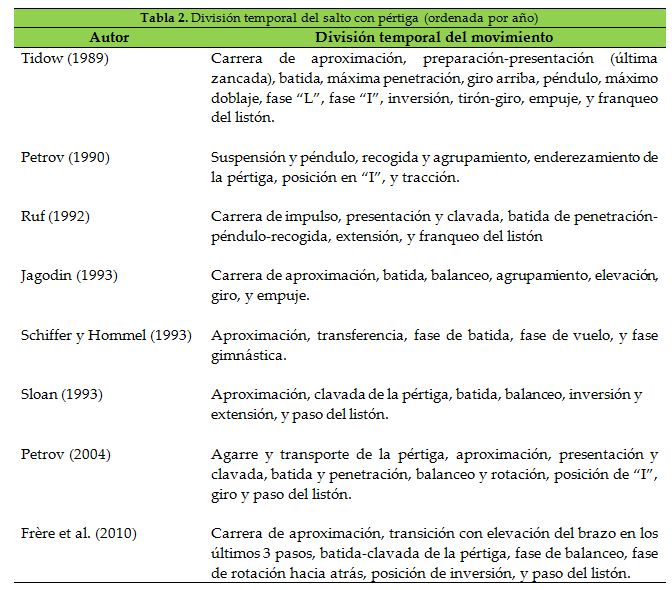
    La división del salto con pértiga en fases temporales es el modelo para la observación de la técnica que utilizan los entrenadores. En la bibliografía existen diversas propuestas (tabla 2), que aunque su denominación de las fases es diferente, a nivel temporal coinciden en gran medida.

    A pesar de la aparición de diferentes propuestas de dividir el gesto técnico para facilitar su análisis, en la actualidad parece que tiene una mayor aceptación la realizada por Tidow (1989) y Petrov (1990) al ser la más empleada en la bibliografía (figura 3).

Figura 3. Secuencia del salto con pértiga (modificado a partir de Petrov, 1990)

3.     Aspectos clave de rendimiento

    En la revisión realizada, existe diversidad de opiniones al respecto. Hay autores que consideran importantes las características antropométricas del saltador referidas al peso y al somatotipo (Liu, Nquanq, y Zhang, 2011; Sullivan, Knowlton, Hetzler, y Woelke, 1994). Otros autores consideran importantes aquellos aspectos relacionados con las características físicas de la pértiga: su longitud y dureza (Dilman y Nelson, 1968; Ekevad y Lundberg, 1995; Grabner, 1997; Linthorne, 2000; Schmolinsky, 1983, en Katsikas et al., 2003; Tidow, 1989), la anchura del agarre (Petrov, 2004, en Zagorac, Retelj, y Katic, 2008) o la altura del agarre (Angulo et al., 1994; Boiko y Nikonov, 1990; Grabner, 1997; Sullivan et al., 1994).

    Por otro lado están los autores que consideran importantes las variables referidas a las diferentes fases temporales del salto. En relación a la fase de carrera de aproximación, la velocidad horizontal de carrera destaca como una variable cinemática determinante en la altura de salto (Adamczewski y Pert, 1997; Armbrust, 1993; Boiko y Nikonov, 1990; Angulo et al., 1994; Christensen y Zebas, 2000; Gros, Adamczewski, y Wolf, 1995; Hay, 1993; Liu y Zhou, 2000; McGinnis, 1997a, 2004; Risk, 2000; Schulek, 1991; Steinacker, 1991; Sullivan et al., 1994), siendo más importante la velocidad que se logra en la parte final de la carrera (Linthorne, 2000).

    En relación a la fase de batida, esta fase es considerada como la más importante de todo el movimiento (Falk, 1993, 1997; Launder, 1989; Linthorne, 1994; Liu, Li, y Wang, 2002; McGinnis, 1997b, 2000; Staveley, 1983; Zhou y Liu, 2000), destacando la cantidad de velocidad horizontal y vertical del CM al final de la batida como los aspectos más importantes de esta fases (Angulo et al., 1994). Estas variables están influenciadas por la velocidad en la carrera de aproximación (Falk, 1993; Tenke, 1991).

    Existen referencias que destacan la importancia del trabajo del atleta en la pértiga tras la batida (Arampatzis et al., 2004; Armbrust, 1993; Botcharnikov, 1996; Dilman y Nelson, 1968; Ekevad y Lundberg, 1995; Gros y Kunkel, 1990; Hubbard, 1980; Jagodin, 1993; Linthorne, 1994; Liu y Wu, 1993; Schade, Arampatzis, y Bruggemann, 1998, 2006; Stepp, 1977; Zagorac et al., 2008). Estas acciones que realiza el pertiguista tras la batida se basan en la teoría de conservación de la energía (Armbrust, 1993; Linthorne, 1989) y permiten incrementar el rendimiento final, otorgándole un impulso extra que permite transformar la energía cinética de carrera (velocidad horizontal) en energía potencial (Ekevad y Lundberg, 1995; Linthorne, 2000) y que permite utilizar pértigas más rígidas (Jagodin, 1993). Esto se debe (teoría de conservación de la energía) a que: cuando la pértiga comienza a doblarse se produce una reducción en la energía mecánica que es causada por la reducción en la energía cinética, que alcanza su mínimo en el momento de máximo doblamiento de la pértiga (cuando el saltador se encuentra agrupado con la espalda paralela al suelo). A partir de este momento y hasta la posición de “I” se produce un incremento progresivo de la energía mecánica que es causado por el incremento en la energía potencial (Frère et al., 2010).

    En relación a la fase de vuelo tras la suelta de la pértiga al realizar el empuje final, existen referencias que defienden la importancia de esta fase en la eficacia del salto (Huffman, 1996). Por último hay autores que consideran importantes la relación entre varios parámetros sobre el rendimiento. McGinnis (1997b) afirma que la máxima altura del salto se logra: a) cuanto más alto y rápido se mueva el CM hacia arriba, b) cuanto mayor sea el empujé-tirón hacia arriba, y c) cuanto menor sea la pérdida de energía. Locatelli (1987) concluye que la relación entre la velocidad horizontal generada durante la carrera y la velocidad vertical dada al CM al final de la batida determinan la altura del salto.

4.     Consideraciones y valores de los aspectos clave de rendimiento

    A continuación se exponen los valores encontrados para los aspectos clave de rendimiento en la prueba de salto con pértiga y las principales consideraciones a tener en cuenta en cada uno de los siguiente apartados: a) en relación al saltador, b) en relación a la pértiga, c) en relación a la carrera de aproximación, d) en relación a la batida, y e) en relación a las fases posteriores a la batida.

4.1.     En relación al saltador

    Locatelli (1987) define las características fundamentales del saltador de pértiga. Estas características corresponden a una tipología longilínea, una estatura entre 1.80-1.90 m, y un peso entre 72-82 kg. Ruf (1992) determina que el pertiguista debe tener las siguientes características: elevada velocidad, buena batida, elevada capacidad física de fuerza, coordinación, buenas condiciones gimnásticas, gran envergadura, pies formados y grandes, columna vertebral bien formada, y valentía, paciencia, y constancia. Johnson (1986) destaca la importancia en la capacidad física de fuerza. En este sentido, Jones (1992) fija la edad de 15 años como adecuada para iniciarse en la especialización de la prueba.

4.2.     En relación a la pértiga

    En este apartado se pueden encontrar referencias a tres aspectos: a) longitud de la pértiga y dureza, b) anchura del agarre, y c) altura del agarre. En relación a la longitud de la pértiga, la bibliografía fija un valor de referencia para atletas de rendimiento de nivel internacional en torno a los 5-5.2 m para los hombres (Grabner, 1997; Linthorne, 2000) y en torno a los 4.30-4.60 m para las mujeres (Bartonietz y Wetter, 1997). Para la dureza de la pértiga se estima que su valor debería tener un valor que fuera 20 kg mayor que el peso del atleta (Tidow, 1989).

    En relación a la anchura de agarre, se trata de un aspecto importante para el desarrollo de una elevada velocidad de carrera (Petrov, 2004) y cuyo valor se fija en un rango amplio. Su valor puede oscilar desde los 0.46-0.48 m (García-Fogeda y Matas, 2005) o 0.49 m (Grabner, 1997) hasta los 0.58 m (Angulo et al., 1994), 0.60-0.70 m (Nikolov, 1986; Petrov, 2004; Tidow, 1989), o los 0.65-0.75 m (Adamczewski y Pert, 1997). Este aspecto depende del género, del nivel de desarrollo de las capacidades físicas (fuerza y velocidad), o nivel de rendimiento del deportista.

    En relación a la altura del agarre, se trata de una variable de rendimiento que debería aumentar junto con su dureza al incrementar la altura del listón (Ruf, 1999). En hombres, su valor se fija en un valor que va desde los 4.90 m (Linthorne, 2000; Locatelli, 1987; Schade et al., 2007) hasta los 5.15-5.20 m (Linthorne, 2000; Locatelli, 1987; Tidow, 1989). En mujeres, se han obtenido mediciones que van desde los 4.05-4.35 m (Bartonietz y Wetter, 1997) hasta los 4.35-4.45 m (Adamczewski y Pert, 1997). Estos valores suponen distancias entre 0.15-0.46 m desde el tope de la pértiga (Falk, 1993).

4.3.     En relación a la carrera de aproximación

    El objetivo de la carrera de aproximación es generar la mayor cantidad de velocidad horizontal (Frère et al., 2009; Linthorne, 2000; Schade et al., 2007) y preparar la clavada de la pértiga en el cajetín (Angulo et al., 1994). Estos dos objetivos se pueden cumplir con una longitud de carrera adecuada.

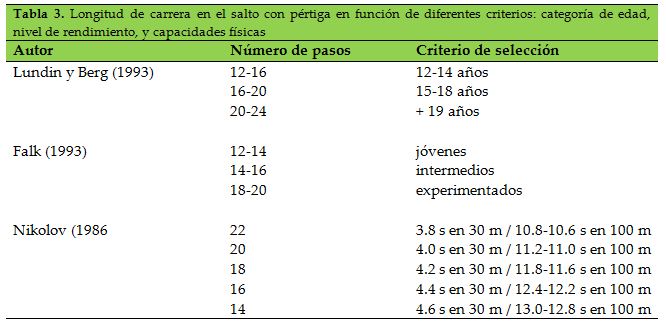
    En relación a su longitud, el número de pasos es menor en comparación con otras pruebas de salto como la longitud o el triple salto. El número de pasos de carrera oscila entre 16-22 pasos (Locatelli, 1987), estando las mujeres más próximas al valor más bajo (Bartonietz y Wetter, 1997). Para los hombres, la carrera típica está compuesta por 18-20 pasos (Bartonietz y Wetter, 1997; Grabner, 1997; Petrov, 2004; Tidow, 1989; Yagodin y Papanov, 1986). Este número de pasos se corresponde con una distancia entre 36 m (Nikolov, 1986) y 42-46 m (Nikolov, 1986; Petrov, 2004) para los hombres y 28-32 m para las mujeres (Nikolov, 1986). También se puede encontrar propuestas de longitudes de carrera en función de la categoría de edad (Lundin y Berg, 1993), del nivel de rendimiento (Falk, 1993), o de las capacidades físicas en diferentes test de velocidad de 30 y 100 m (Nikolov, 1986) (tabla 3).

    En relación a la velocidad de carrera, esta no es máxima porque: a) se transporta un implemento (la pértiga), y b) por los requerimientos propios de la batida. Sin embargo, a mayor velocidad de carrera, mayor deformación de la pértiga, y mejores disposiciones para realizar un agarre alto de la pértiga (Angulo et al., 1994). Se han medido velocidades máximas de 8.96-8.70 m/s en saltadores de nivel nacional (García-Fogeda y Matas, 2005). En saltadores de nivel internacional esta velocidad se fija en torno a los 10 m/s para hombres (Gros y Kunkel, 1990; Locatelli, 1987; Nikolov, 1986; Petrov, 2004; Tidow, 1989; Yagodin y Papanov, 1986) o algo menos 8.8-9.4 m/s (Schade et al., 2007) y 8 m/s para las mujeres (Adamczewski y Pert, 1997; Bartonietz y Wetter, 1997; Schade et al., 2007). Esta velocidad se reduce hasta los 8-8.5 m/s al clavar la pértiga (Locatelli, 1987). La máxima velocidad de carrera se alcanza 6-8 m antes de producirse la batida (Nikolov, 1986).

    En relación a la preparación para la batida, el último paso de carrera es el más corto y durante el penúltimo paso se produce un descenso en el CM del saltador (Angulo et al., 1994), provocado por un incremento en la longitud del paso (García-Fogeda y Matas, 2005), cuya longitud se fija en un valor medio de 2 m. Durante este paso, la velocidad de carrera se reduce en valores que llegan hasta los 2 m/s de media (Angulo et al., 1994; Gros y Kunkel, 1990, McGinnis, 1987; Tidow, 1989), lo que en la práctica ha dado mediciones de 8.95-9.74 m/s (Angulo et al., 1994) y 8.32-8.66 m/s (García-Fogeda y Matas, 2005).

4.4.     En relación a la batida

    Debido a las propiedades elásticas de la pértiga, en la batida se dan dos objetivos: a) incrementar el tiempo del último apoyo para resistir la fuerza de reacción de la pértiga y b) incrementar el ángulo de la pértiga con la horizontal (Morlier y Mesnard, 2007). Esto último se logra con una elevación del brazo dominante, el brazo superior (Frère et al., 2009). Además, se debe conseguir trasferir la mayor cantidad de energía acumulada durante la carrera.

    El posicionamiento del pie de batida se realiza en la perpendicular del agarre de la mano superior en el momento del contacto (Tidow, 1989) o ligeramente retrasado (Angulo et al., 1994). La distancia entre el pie de batida y el cajetín oscila entre 3.78 m (García-Fogeda y Matas, 2005), hasta 4.10-4.20 m (Adamczewski y Pert, 1997; García-Fogeda y Matas, 2005; Grabner, 1997), 4.10-4.30 m (Locatelli, 1987), o 4.20-4.40 m (Petrov, 2004). La pérdida de velocidad horizontal en este apoyo puede oscilar entre 0.5 m/s (Linthorne, 2000) hasta algo más de 1 m/s (García-Fogeda y Matas, 2005; Gros y Kunkel, 1990). Los principales factores que influyen en esta pérdida de velocidad son la necesidad de transformar la energía de carrera y el impacto de la punta de la pértiga en el cajetín (Frère et al., 2010).

    Durante la batida, la forma en la que actúan los brazos es opuesta, es decir, el brazo superior ejerce presión sobre la pértiga hacia delante hacia abajo, mientras que el brazo inferior ejerce presión hacia delante y hacia arriba (Dapena y Braff, 1983; Morlier y Mesnard, 2007).

    En relación a la velocidad horizontal al final de la batida, se han medido valores de 7.24-7.34 m/s (García-Fogeda y Matas, 2005), 8.17 y 8.6 m/s (Angulo et al., 1994; Grabner, 1997), o 8.55 m/s (Yagodin y Papanov, 1986). La cantidad de velocidad horizontal es mayor que la cantidad de velocidad vertical. Esta velocidad vertical se fija en 2 m/s (Grabner, 1997) hasta 2.61-3.35 m/s (García-Fogeda y Matas, 2005). La velocidad resultante es de 7.69-8.06 m/s (García-Fogeda y Matas, 2005) hasta los 8.8 m/s (Grabner, 1997). Esta velocidad se reduce cuando se incrementa el ángulo de batida (Linthorne, 2000). En relación al ángulo de despegue del atleta al final de la batida se fija en 16-18º (Locatelli, 1987), 18º (Linthorne, 2000). La duración de la fase de batida es de 0.115-0.140 s (Locatelli, 1987).

4.5.     En relación a las fases posteriores a la batida

    Tras el despegue y el agrupamiento, la pértiga alcanza su mayor doblaje entre 1.5-1.6 m de su longitud total (Angulo et al., 1994), lo que supone un 20.9-18.3% de acortamiento (Grabner, 1997). La velocidad horizontal y vertical del CM, que durante la batida se encontraban dispares, se igualan cuando el saltador se encuentra agrupado con la espalda paralela al suelo (máximo doblamiento de la pértiga). A partir de este momento, la velocidad vertical se incrementa hasta alcanzar la posición de inversión “I” (Angulo et al., 1994; Gros y Kunkel, 1990). Esta velocidad oscila entre 4.40-4.75 m/s (García-Fogeda y Matas, 2005) y 5.01-5.21 m/s (Angulo et al., 1994; Grabner, 1997). En la posición de “I”, la cantidad de velocidad vertical es la máxima de todo el movimiento (Hay, 1993). La fase sobre la pértiga representa el 63-71% del total de la altura de salto (Grabner, 1997). Esta acción supone una duración de 1.18-1.52 s.

    Para que el saltador aproveche al máximo el impulso de la pértiga, este debería situarse por encima de la misma al final del tirón-empuje, antes de la suelta (Angulo et al., 1994). La diferencia entre la altura del agarre y la máxima altura del CM, menos 20 cm de la caja (índice de eficacia) en hombres entre 0.80-1 m (Locatelli, 1987) hasta 1.37 m y en mujeres entre 0.15 y 0.55 m (Grabner, 1997; Adamczewski y Pert, 1997). En saltadores nacionales de 0.35-0.50 m (García-Fogeda y Matas, 2005). Durante la fase de paso del listón, la cantidad de velocidad vertical del CM es nula o próxima a cero (Angulo et al., 1994; Gros y Kunkel, 1990). La altura máxima del CM se fija entre 5.25-5.54 m (García-Fogeda y Matas, 2005) y 5.66-5.91 m (Angulo et al., 1994; Grabner, 1997).

5.     Conclusiones o aportaciones

    Este artículo puede servir de ayuda a atletas, entrenadores, e investigadores que tengan como objetivo aumentar la comprensión teórica de la prueba o la mejora del rendimiento. La información que aquí se recoge representa el resultado de un trabajo de revisión de los artículos de la bibliografía a nivel nacional e internacional con mayor relevancia. Los datos expuestos pueden servir de referencia para adaptar la forma de ejecutar la técnica a las características personales del deportista y al entrenador para realizar la tarea de observación del movimiento.

Bibliografía

Adamczewski, H. y Pert, B. (1997). Run-up velocities of female and male pole vaulting and some technical aspects of women´s pole vault. New studies in athletics, 12(1), 63-76.

Angulo, R. M., Kinzler, S. B., Balius, X., Turro, C., Caubet, J. M., Escoda, J., y Prat, J. A. (1994). Biomechanical analysis of the pole vault event. Journal of Applied Biomechanics, 10(2), 147-165.

Anderson, G. K. (1997). The limits of human performance in the pole vault. Track Coach, 138, 4412–4415, 4421.

Arampatzis, A., Schade, F., Brüggemann, G. P. (1997). Pole Vault. En: Müller, H. y Hommel, H. (Eds.), Biomechanical Research Project at the VIth World Championships in Athletics, Athens 1997: Preliminary Report. New Studies in Athletics, 12(2), 43-73.

Arampatzis, A., Schade, F., y Bruggemann, G. P. (2002). Interaction between the pole and the human body and its effect on the pole vaulting performance. XXVII Symposium of the International Society of Biomechanics in Sports. Caceres: Spain, pp. 298-301.

Arampatzis, A., Schade, F., y Bruggemann, G. P. (2004). Effect of the pole-human body interaction on pole vaulting performance. Journal of Biomechanics, 37(9), 1353-1360.

Armbrust, W. (1993). Energy conservation in pole vaulting. Track Technique, 125, 3991-3994, 4005.

Attig, R. (1987). Understanding pole vault mechanics. Track and Field Quarterly Review, 4, 25-32.

Bartonietz, K. y Wetter, J. (1997). Analysis of the International situation in women´s pole vault. New Studies in Athletics, 12(1), 15-21.

Boiko, V. y Nikonov, J. (1990). Something new in the pole vault. Modern athlete and coach, 28(4), 11-13.

Bosen, K. O. (1972). Comparison of rigid and flexible pole vaulting technique. In F. Wilt (Ed.), The jumps: Contemporary theory, technique and training (pp. 55-67). Los Altos, CA: Tafnews Press.

Botcharnikov, R. (1996). The continuous chain model in the pole vault. Track Coach, 135, 4301-4304.

Bruggemann, G. P., Schade, F., y Arampatzis, A. (1999). Pole vault. Biomechanical research project Athens 1997 (pp. 145-156). Meyer and Meyer Sport.

Burgess, S. C. (1998). The modern Olympic vaulting pole. Materials and Design, 19(5), 197-204.

Carr, G. (1999). Fundamentals of track and field, 2nd ed. Champaign, IL: Human Kinetics.

Christensen, B. y Zebas, C. (2000). A comparison of practice and competition approach velocities and the position of the top handhold at the pole plant in pole vaulters. XVIII Symposium of the International Society of Biomechanics in Sports. Hong Kong: China.

Dapena, J. y Braff, T. (1983). Use of separate hand location to calculate ground reaction force exerted on a vaulting pole. Medicine and Science in Sports and Exercise, 15(4), 313-318.

Dillman, C. J. y Nelson, R. C. (1968). The mechanical energy transformations of pole vaulting with a fibreglass pole. Journal of Biomechanics, 1(3), 175-183.

Ekevad, M. y Lundberg, B. (1995). Simulation of “smart” pole vaulting. Journal of Biomechanics, 28(9), 1079-1090.

Ekevad, M. y Lundberg, B. (1997). Influence of Pole Length and Stiffness on the Energy Conversion in Pole Vaulting. Journal of Biomechanics 30(3), 259-264.

Falk, B. (1993). The continuous chain method for improving pole vault performance. New Studies in Athletics, 8(1), 57-59.

Falk, B. (1997). Developing a dynamic pole vault takeoff. Track and Field Coaches Review, 2, 18.

Frère, J., Chollet, D., y Tourny-Chollet, C. (2009). Assessment of the influence of pole carriage on sprint kinematics: A case study of novice athletes. International Journal of Sports Science and Engineering, 3(1), 3-10.

Frère, J., Hermette, M., Slawinski, J., y Tourny-Chollet, C. (2010). Mechanics of pole vaulting: a review. Sports Biomechanics, 9(2), 123-138.

García-Fogeda, A. y Matas, S. (2005). Análisis cinemático de los tres mejores saltos en el concurso de salto con pértiga realizado en el campeonato de España al aire libre del año 2003. Kronos, 7, 33-37.

Grabner, S. (1997). Kinematic analysis of the women.s pole vault. New studies in athletics, 12(1), 47-61.

Gros, H. J. y Kunkel, V. (1990). Biomechanical analysis of the pole vault. Biomechanical Analyses of the jumping events time analysis of the sprint and hurdle events (IAAF). New Studies in Athletics (Suplement), 1, 219-260.

Gros, H. J., Adamczewski, H., y Wolf, J. (1995). Biomechanical aspects of the pole vault: analysis of the 4th IAAF World Championships. En: Barabas, A.; Fabian, G. (Eds.): Biomechanics in sports XII: Proceedings of the 12th Symposium of the International Society of Biomechanics in Sports. Budapest: International Society of Biomechanics in Sports, 1995, pp. 354-356.

Gros, H. J. y Terauds, J. (1983). Applications of biomechanics cinematography to research and coaching aspects of the pole vault. I Symposium of the International Society of Biomechanics in Sports. San Diego, California: USA, 269-277.

Hay, J. (1993). The Biomechanics of Sports Techniques. New Jersey: Prentice Hall.

Houvion, M. (1984). Perfeccionamiento de la técnica del salto con pértiga. Saltos II (pp. 41-66). Madrid: Centro de Documentación de la Escuela nacional de Entrenadores. Real Federación Española de Atletismo.

Hubbard, M. (1980). Dynamics of the pole vault. Journal of Biomechanics, 13 (11), 965-976.

Huffman, S. (1986). The spin doctor. Track and Field Coaches Review, 95 (4), 16-17.

IAAF (2012). Competition Rules 2012-2013. International Association of Athletic Federations.

Jagodin, V. (1973). Modern pole vaulting. Modern Athlete and Coach, 11(1), 27-30.

Jagodin, V. (1993). Sergei Bubka above the bar. Modern Athlete and Coach, 31(2), 22-25.

Johnson, D. (1986). Women's pole vault and triple jump. Athletics Coach, 4, 24-27.

Jones, M. (1992). The case for lowering the minimum age for female pole vaulting to 15 years. Athletics Coach, 26(2), 15-16.

Katsikas, F., Papaiakovou, G., Pilianidis, T., y Kollias, I. (2003). Pole vault as "double pendulum" and "penetration". Modern Athlete and Coach, 41(3), 17-20.

Launder, A. (1989). The pre-jump - a revolution in the Pole Vault. Modern Athlete and Coach, 27(3), 7-9.

Launder, A. y Linthorne, N. P. (1990). The pre-jump. Track Technique, 112, 3991-3995.

Linthorne, N. P. (1989). The fibreglass pole. Modern Athlete and Coach, 27(1), 15-19.

Linthorne, N. P. (1994). Mathematical model of the takeoff phase in the pole vault. Journal of Applied Biomechanics, 10(4), 323-334.

Linthorne, N. P. (2000). Energy loss in the pole vault take-off and the advantage of the flexible pole. Sports Engineering, 3(4), 205-218.

Liu, X., Li, S., y Wang, X. (2002). Biomechanical analysis of the top chinese female pole vaulters. XX Congress of the International Society of Biomechanics. Caceres: Spain, pp 141-143.

Liu, G., Nquanq, S. K., y Zhang, Y. (2011). Pole vault performance for anthropometric variability via a dynamical optimal control model. Journal of Biomechanics, 44(3), 436-441.

Liu, Y. y Wu, Y. (1993). The energy analysis of the pole vault. XIV Congress of the International Society of Biomechanics. Francia: Paris, pp 806-807.

Liu, X. y Zhou, T. (2000). Biomechanical analysis on run-up and take-off in women’s pole vault. XVIII Symposium of the International Society of Biomechanics in Sports. Hong Kong: China.

Locatelli, E. (1987). Technical and methodological considerations on the jumps. New Studies in Athletics, 2(2), 23-40.

Lundin, P. y Berg, W. (1993). Developing the approach in the jumps. New Studies in Athletics, 8(1), 45-50.

McGinnis, P. M. (1987). Performance limiting factors in the pole vault. Medicine and Science in Sports and Exercise, 19(2), 18.

McGinnis, P. M. (1997a). Approach run velocities of female pole vaulters. XV Symposium of the International Society of Biomechanics in Sports. Denton, Texas: USA, 101-105.

McGinnis, P. M. (1997b). Mechanics of the pole vault take-off. New Studies in Athletics, 12(1), 43-46.

McGinnis, P. M. (2000). Eight elements of an effective takeoff. In J. Jarver, (Ed.), The jumps: Contemporary theory, technique and training, 5th ed. (pp. 84-87). Mountain View, CA: Tafnews Press.

McGinnis, P. M. (2004). Evolution of the relationship between performance and approach run velocity in the women’s pole vault. XXII Symposium of the International Society of Biomechanics in Sports. Ottawa: Canada, pp. 531-534.

Morlier, J. y Mesnard, M. (2007). Influence of the moment exerted by the athlete on the pole in pole-vaulting performance. Journal of Biomechanics, 40(10), 2261-2267.

Nikolov, J. (1986). The pole vault run-up. Modern Athlete and Coach, 24(2), 7-9.

Petrov, V. (1990). Consideraciones sobre la técnica y el entrenamiento del salto con pértiga. Cuaderno de atletismo de la Real Federación Española de Atletismo. 29: 21-44.

Petrov, V. (2004). Pole vault – the state of the art. New Studies in Athletics, 19(3), 23-32.

Risk, B. (2000). Groundwork for the pole vault. In J. Jarver, (Ed.), The jumps: Contemporary theory, technique and training, 5th ed. (pp. 88-90). Mountain View, CA: Tafnews Press.

Ruf, H. (1992). Salto con pértiga. En Bravo, J.; Ruf, H.; Vélez, M. (Eds.) Atletismo II: Saltos (pp. 101-177). Madrid: RFEA.

Russomanno, T. G., Rossetto, N. P., y Barros, R. M. L. (2009). 3D kinematical analysis of Brazilian female pole vaulters. XXVII Symposium of the International Society of Biomechanics in Sports. Limerick: Ireland.

Schade, F., Arampatzis, A., y Bruggemann, G. P. (1998). Biomechanical analysis of the pole vault at the VIth World Championships in Athletics. XVI Symposium of the International Society of Biomechanics in Sports. Konstanz: Germany, pp. 243-246.

Schade, F., Arampatzis, A., y Bruggemann, G. P. (2000). Influence of different approaches for calculating the athlete’s mechanical energy on energetic parameters in the pole vault. Journal of Biomechanics, 33(10), 1263-1268.

Schade, F., Arampatzis, A., y Bruggemann, G. P. (2006). Reproducibility of energy parameters in the pole vault. Journal of Biomechanics, 39(8), 1464-1471.

Schade, F., Isolehto, J., Arampatzis, A., Bruggmann, G. P., y Komi, P. (2007). Biomechanical analysis of the pole vault at the 2005 IAAF World Championship in Athletics. New Studies in Athletics, 22(2), 29-45.

Schiffer, J. y Hommel, H. (1993). The XVIIth Congress of the European Athletics Coaches Association – The Jumping Events. New Studies in Athletics, 8(2), 95-103.

Schulek, A. (1991). Changing speed and technique priorities in the training of jumpers. Track and Field Quarterly Review, 91(4), 39-41.

Sloan, R. (1993). Mechanics of the pole vault. Track and Field Quarterly Review, 93(4), 38-39.

Staveley, B. (1983). The most critical phase in the pole vault. Track and Field Journal, 19, 26-28.

Steinacker, U. (1991). The run-up speed in the Pole Vault. Modern Athlete and Coach, 29(2), 14-16.

Stepp, R. D. (1977). An orderly approach to the mechanics of the pole vault. Modern Athlete and Coach, 15(2), 13-17.

Sullivan, J. J., Knowlton, R. G., Hetzler, R. K., y Woelke, P. L. (1994). Anthropometric characteristics and performance related predictors of success in adolescent pole vaulters. Journal of Sports medicine and Physical Fitness, 34(2), 179-184.

Tenke, Z. (1991). The primary importance of speed and technique in preparation for the jumps. Track and Field Journal de l'athletisme, 39, 27-29

Tidow, G. (1989). Model technique analysis sheet for the vertical jumps. Part III: The pole vault. New Studies in Atheletics, 4(4), 43-58.

Wang, D. (2000). Application of high Speedy panning on the technical analysis of pole vault. XVIII Symposium of the International Society of Biomechanics in Sports. Hong Kong: China.

Yagodin, V. y Papanov, V. (1986). Sergey Bubka - 6.01m. Modern Athlete and Coach, 25(4), 12-14.

Zagorac, N., Retelj, E., y Katic, R. (2008). Successful pole vault influenced by certain kinematical parameters. Collegium Antropologicum, 32(4), 1133-1139.

Zhou, T. y Liu, X. (2000). Biomechanical análisis of elite chinese female pole vaulters take-off techniques. XVIII Symposium of the International Society of Biomechanics in Sports. Hong Kong: China.

Otros artículos sobre Biomecánica

	Búsqueda personalizada
EFDeportes.com, Revista Digital · Año 17 · N° 168 \| Buenos Aires, Mayo de 2012 © 1997-2012 Derechos reservados