Momento angular en la fase de despegue de la barra en el levantamiento de pesas en la modalidad de arranque
	Ministerio del Poder Popular para el Deporte Laboratorio de Biomecánica (Venezuela)	Marco Gómez ttgomez2004@yahoo.com Sol Patricia Beltrán marpatt822@hotmail.com
	Resumen           El objetivo del presente análisis fue valorar, desde el punto de vista cuantitativo, la aplicación del momento angular (torque) en la fase de despegue de la barra en el levantamiento de pesas olímpico en la modalidad de arranque en la ejecución de tres (3) atletas de la categoría de 48 Kg en la mencionada disciplina deportiva. Para la videograbación se utilizaron dos cámaras digitales de 30 Hz, marca Panasonic modelo PV-GS35. Las cámaras fueron ubicadas a 45° del plano frontal en el que se realizaron las ejecuciones. Se utilizó el software Hu-m-an V.5.0, para el procesamiento de los videos y la obtención de los resultados de las diferentes variables. Se sincronizaron los videos de cada cámara y las escalas de forma tridimensional. A través de algoritmos de Transformación Lineal Directa (DLT), posteriormente, se crearon archivos 2D, en los que se despliegan cálculos cinéticos. Luego de realizar los cálculos biomecánicos referentes al torque, se concluyó que para lograr una mayor ventaja mecánica la altura de las caderas debe estar en un posición similar al de las rodillas en la posición inicial, disminuir la fuerza aplicada y vencer por tanto con mayor facilidad la inercia (masa) de la barra que se encuentra en reposo.           Palabras clave: Despegue. Torque. Arranque. Ventaja mecánica.
	EFDeportes.com, Revista Digital. Buenos Aires, Año 16, Nº 160, Septiembre de 2011. http://www.efdeportes.com/

1 / 1

Introducción

    Es necesario conocer cómo se producen los diferentes movimientos del cuerpo humano en la práctica deportiva con el fin de reconocer cuando se produce una ejecución más efectiva al cambiar alguna variable biomecánica. Resulta complejo analizar las causas que producen dichos movimientos y más aún considerar la influencia de un implemento deportivo, como lo es, en este caso específico, sobre la acción en la fase de despegue de la barra en levantamiento de pesas olímpico.

    El despegue de la barra de la plataforma de competencia se limita al instante en el que se pierde contacto, a partir de la aplicación de fuerzas internas que dan inicio al movimiento y fuerzas que se manifiestan entre otras formas como palancas para el deporte analizado en este estudio. Según Campillo, Chollet y Micallef (1997) señalan que es difícil optimizar las posiciones angulares de los segmentos de los atletas, velocidades de ejecución entre otros aspectos. Sin embargo, al hacer uso de las ciencias aplicadas al deporte, específicamente la biomecánica, se pueden realizar un modelo, por ejemplo, el despegue de los pesos del suelo con el fin de mejorar los resultados deportivos. Aguado (2001) menciona que en los diferentes movimientos del cuerpo humano se ponen de manifiesto diferentes tipos de palancas que constan de articulaciones las cuales son consideradas como los puntos de apoyo, los músculos agonistas que son aquellos que producen la fuerza que permiten mover la palanca, y la resistencia que podría ser un objeto externo, el propio peso del cuerpo o la relación de ambos, lo cual funciona según sea el objetivo que se persigue en cada movimiento. Boone y Col, (2009) explica que tres puntos determinan el tipo de palanca, el apoyo (fulcro), la resistencia y la fuerza aplicada. En el cuerpo humano se manifiestan tres tipos de palancas, como se muestra en la Figura 1 algunos ejemplos:

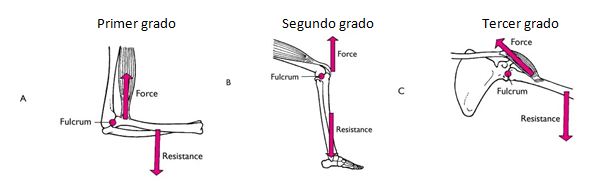
Figura 1. Tipos de palanca: Tomada de kinesiology.boisestate.edu/rvhp/KINES370/Chapter%2013.ppt (2009)

    La diferencia de clases de palancas se manifiesta en tres variables mecánicas importantes como la fuerza, velocidad y rango de movimiento. Ozkaya y Nordin (1998), explican que una fuerza aplicada sobre un objeto puede trasladar, rotar y/o deformar el mismo. Cuando la aplicación de la fuerza es a un extremo del centro de masa del objeto, esta genera un movimiento rotatorio y si se encuentra unido a un punto fijo estamos en presencia de una palanca, este efecto rotatorio se denomina torque o momento de una fuerza (T=FxD). Según Guede (2011), el torque o momento de fuerza angular en el cuerpo humano indica la cantidad de fuerza necesaria para producir un movimiento angular de una palanca; por tanto, es el producto de la magnitud de la fuerza aplicada (F) por la distancia (d) perpendicular entre la línea por donde pasa el vector de la aplicación de fuerza, y el eje de giro. Ampliando un poco más el concepto, Inzunza (2007) señala que el torque es una magnitud vectorial y, por lo tanto, se debe conocer la dirección de la aplicación de la fuerza (F). De igual forma Lopategui (2000) plantea que el torque se ve afectado por el ángulo de aplicación de la fuerza, por lo que define matemáticamente al torque de la siguiente manera: T= d * F (sen ); en donde d, es la distancia desde el punto de aplicación de la fuerza hasta el eje de giro, F es la fuerza que produciría la rotación y (sen ) es el factor que indica la dirección de la fuerza respecto del eje de coordenadas.

    Para el levantamiento de pesa olímpico y en especial para el despegue de la barra se pone de manifiesto la aplicación en los diferentes segmentos que intervienen en la acción del torque. Szklarz (2010) plantea que al aplicar una palanca de segunda clase se busca mayor ventaja mecánica, ya que, esto puede ayudar en la reducción de aplicación de la fuerza para levantar más peso (resistencia).

    Molano (2008) señala que desde el punto de vista matemático la ventaja mecánica se puede expresar a través de la siguiente fórmula: Ventaja mecánica= Brazo de Fuerza / Brazo de Resistencia. Así mismo, Thompson y Floyd (1994) proponen que la ventaja mecánica está relacionada con el momento de rotación, si la fuerza es igual a la masa y el brazo de fuerza es mayor que el de resistencia, entonces la fuerza tiene la ventaja y el objeto rotara en dirección de la fuerza. En el mismo orden de idea, Izquierdo (2008) considera que el momento de fuerza o torque se obtiene de la relación entre la fuerza aplicada y su brazo de palanca (distancia perpendicular entre el vector de fuerza aplicada y el eje de giro), el cual es el que permite que se produzca la rotación de un objeto. Así mismo, Guede (2011) señala que el momento de fuerza angular en el cuerpo humano indica la cantidad de fuerza necesaria para producir un movimiento angular de una palanca, los cuales se producen por las rotaciones de los diferentes segmentos corporales alrededor de las articulaciones del cuerpo.

    Así como en los diferentes movimientos del cuerpo humano, los aspectos biomecánicos contemplados en el área de la cinética se ponen de manifiesto en la realización de diferentes destrezas en el ámbito deportivo, las cuales pueden ser aplicadas y entrenadas para mover un gran peso con la aplicación de poca fuerza, aspecto importante a considerar en levantamiento de pesas olímpico y en especial en la fase de despegue de la barra donde la misma se encuentra en posición de reposo (inercia) y posee una velocidad inicial cero (0 m/s). En tal sentido, Schilling y Col (2008) explican que: “a medida que la velocidad se aproxima a cero, la fuerza propulsiva se acerca igualmente a cero y, por lo tanto, el movimiento lento de objetos solo requerirá de una fuerza aproximadamente igual al peso de la carga”.

    Autores como Enoka (1979), Burdett (1982), Baumann et al., (1988) y Garhammer et al., (1989) mencionan que el uso de materiales videográficos permiten observar y comparar las diferentes técnicas a emplear en el levantamiento de pesas olímpico y, a su vez, se pueden cuantificar las fuerzas que el atleta debe aplicar para levantar la barra en el plano vertical.

    Se realizó la presente investigación con el fin de analizar cuantitativamente a través de material videográfico la aplicación de torque en la fase de despegue de la barra de levantamiento de pesas olímpico, de tres (3) atletas de la categoría de 48 Kg, sexo femenino, en esta disciplina deportiva.

Método

Sujetos

    Los sujetos fueron tres (3) atletas de sexo femenino que compiten en la categoría de 48 Kg de peso corporal. Sujeto 1 ocupó el segundo lugar en los Juegos Olímpicos Beijing 2008 y también en el Campeonato Mundial de Antlanya (Turquía) de 2010, el intento analizado obtuvo el primer lugar en el podio con 84 kg de peso en la barra. El Sujeto 2 obtuvo la medalla de oro tanto en el Campeonato Panamericano de 2010 como en los Juegos Centroamericanos y del Caribe realizado el mismo año; se seleccionó el levantamiento de 77 kg. El Sujeto 3 obtuvo el primer lugar en los Juegos Sudamericanos de 2010, el levantamiento analizado fue de 70 kg.

Videograbación

    Se utilizaron dos cámaras digitales de 30 Hz, marca Panasonic modelo PV-GS35. Las cámaras fueron ubicadas a 45° del plano frontal en el que se realizaron las ejecuciones.

Procesamiento

    Se empleó el software de análisis de movimiento Hu-m-an V 5.0, utilizando el protocolo de procesamiento tridimensional. Fue utilizado para la sincronización de las cámaras la Transformación Directa Lineal (DLT).

    Las variables calculadas fueron: Fuerza, Torque, brazo momento (fuerza y resistencia).

    Los valores de fuerza aplicada por los grupos musculares que componen la cadena biocinemática de miembros inferiores, cabe mencionar, los segmentos con los cuales se debe realizar el despegue y segundo halón para evitar lesiones en la región lumbosacra de la espalda.

    Se consideró la articulación de la rodilla como eje de giro.

    La magnitud de la fuerza aplicada por el Centro de Gravedad del sistema atleta-barra, con la cual se conoce cual es la resistencia a vencer.

Resultados

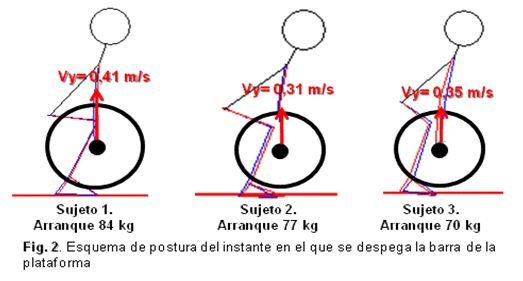
Discusión

    En la Figura 2 se visualiza el esquema de postura en el instante cuando se despega la barra de la plataforma de competencia, momento en el cual se calcula la fuerza de resistencia (de pesos segmentales del cuerpo de la atleta sumado al peso de la barra) y la aplicación de la fuerza muscular que se debe emplear para vencer la resistencia.

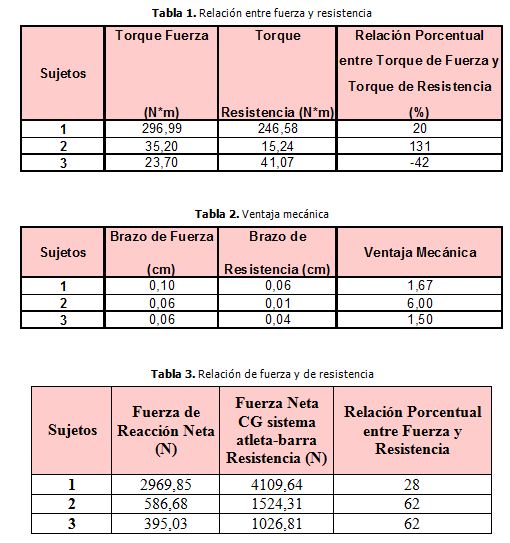
    En la Tabla 1, se presenta la relación porcentual entre el torque de fuerza y el torque de resistencia. En el caso del Sujeto 1 se aplicó 20% del momento de la fuerza para vencer el de la resistencia; sin embargo, la magnitud de los torques es grande en comparación con los resultados obtenidos con los otros dos sujetos (2 y 3). Esto indica que la aplicación del torque es mucho más eficiente que en el caso de los dos atletas, aun cuando los valores son mayores. El Sujeto 2 empleó 131% de torque de fuerza, es decir que se aplicó más del doble del torque de resistencia, lo cual es innecesario, pues se busca emplear el menor esfuerzo posible. El Sujeto 3 utilizó -42% del torque de fuerza para iniciar el movimiento, siendo el torque de fuerza (23,70 N*m) inferior al torque de resistencia (41,07 N*m), esto no se considera correcto porque en esta acción el objetivo no es la velocidad (palanca tercer genero), sino un desplazamiento corto (palanca de segundo genero). La eficiencia y la eficacia en esta acción la consigue el Sujeto 1, ya que realiza menor esfuerzo para cumplir el objetivo de del despegue, coincidiendo de esta manera con lo reportado en los resultados de la investigación de Salaami, Jamshidi, Rostami y Najarian (2008), en la cual hallaron que la reducción de los valores de torque conllevan a levantar un mayor peso.

    Winston (2002) señala que en una palanca de segundo grado o palanca de fuerza existe ventaja mecánica, cuando se realiza un trabajo con la menor fuerza aplicada, para ello es necesario que en proporción el brazo de potencia sea mayor que el de resistencia. Por tanto, al analizar los resultados presentados en la Tabla 2, se puede evidenciar que en el caso del Sujeto 2, el brazo de fuerza fue 6 veces mayor al brazo de resistencia esto no es proporcional. El problema se evidencia en la disminución que se realiza del brazo de resistencia que se encuentra muy cercano al apoyo (fulcro) arriesgando el movimiento a convertir el mismo de una palanca de 2do grado (fuerza) a palanca de primer grado (equilibrio).

    El mayor o menor brazo de resistencia tiene mucha relación con la posición inicial que adoptan los atletas, pues en la medida en que la articulación de las caderas este más alineada (Fig.2) con la articulación de la rodilla y que el segmento tronco se encuentre cercano a los 90 grados con respecto a la horizontal, estos dos aspectos ayudarán al aumento del brazo de potencia y retrasará, por tiempo prolongado, el cambio de palanca (equilibrio) que se manifiesta durante el primer halón.

    En la Tabla 3 se evidencia que el valor neto de aplicación de fuerza de los Sujetos 2 y 3 es mucho menor que en el sujeto 1, lo cual se debe, por una parte, a la distribución de los segmentos y, por otro lado, al peso total de la barra que es mucho mayor en el Sujeto 1. El porcentaje demuestra también que el Sujeto 1 es más eficiente, ya que utilizó poca fuerza para mover una alta resistencia, además, ello contribuye a garantizar el mayor impulso mecánico.

Conclusiones

    La posición inicial del sujeto 1, donde se logra la altura similar de las articulaciones de las caderas-rodillas respecto a la plataforma; el segmento tronco se acerca a los 90 grados, con respecto a la línea imaginaria horizontal antes del despegue de la barra. Estos dos aspectos permiten el logro de un momento angular de la fuerza (torque) mucho menor que la resistencia; allí se logra una ventaja mecánica, pues se alcanza una óptima proporción de los diferentes brazos momentos (fuerza-resistencia).

    La posición descrita anteriormente contribuye con el mayor impulso mecánico al retrasar el cambio de palanca de segundo a primer grado por más tiempo durante el primer halón. Además, el aumento del impulso mecánico es más eficiente en esta fase, no por la aplicación de un gran esfuerzo, sino por el tiempo.

    Finalmente, dicha posición garantiza la acción de la musculatura de los miembros inferiores durante el despegue y el primer halón para vencer la inercia de la barra que representa aproximadamente el doble del peso corporal del sujeto.

Bibliografía

• Aguado, X. (2001). “Guías de las clases de la facultad de ciencias del deporte”. Universidad Castilla-La Mancha. Tema 7. Las fuerzas.

• Schilling, B. Michael J. Falvo and Loren Z.F. Chiu. (2008). “Force-Velocity, Impulse-Momentum Relationships: Implications For Efficacy Of Purposefully Slow Resistance Training”. Journal of Sports Science and Medicine 7, 299 – 304

• Boone, T. y Bimbaum, L. (2009). “La ciencia de las palancas”. Disponible en: http://faculty.css.edu/tboone2/asep/Lever.doc. [Consultado agosto 29, 2011].

• Campillo, P., Chollet, D., Michellef, J.P. (1997). “Evolutions des variables cinematiques et dynamiques lors du tirages á l´arrache en halterophilie. Cinesiologie”. 176. Pp 197-202.

• Enoka, R. (1979), "The pull in Olympic weightlifting", Medicine and Science in Sports, JI, pp. 131-137.

• Guede, F. (2011). “Principios de Biomecánica”. Disponible en: http://es.scribd.com/doc/56282864/1/PRINCIPIOS-DE-BIOMECANICA. [Consultado mayo 25, 2011].

• Inzunza J. (2007). “Introducción a la Mecánica”. Capitulo 6 Torque y equilibrio de cuerpo rígido. Disponible en: http://www2.udec.cl/~jinzunza/fisica/cap6.pdf. [Consultado mayo 25,2011].

• Izquierdo M. (2008). “Biomecánica y bases neuromusculares de la actividad física y el deporte: Momento de una fuerza”. 242. Editorial Médica Panamericana S.A. ISBN 978-84-9835-023-4.

• Lopategui, E. (2000). “Principios de la Biomecánica”. Facultad de Educación, Departamento de Educación Física. Disponible en: http://www.saludmed.com/CsEjerci/Cinesiol/P-Biomec.html. [Consultado mayo 27, 2011].

• Molano J. (2008). “El momento de la fuerza (III): ¿Qué ventaja mecánica nos ofrecen las palancas?” Disponible en: http://www.fuerzaycontrol.com/cuerpo-humano/biomecanica/mecanica-humana/el-momento-de-la-fuerza-iii-que-ventaja-mecanica-nos-ofrecen-las-palancas/. [Consultado mayo 27, 2011].

• Ozkaya, N y Nordin, M. (1998). “Fundamentals of Biomechanics, equilibrium, motion, and deformation: Moment and Torque”. Springer Science Business Media, Inc. 1999. ISBN 0-387-98283-3. P.31

• Salaami F., Jamshidi N., Rostami and Najarian S. (2008). “Power Enhancement of Weightlifters during Snatch through Reducing Torque on Joints by Particle Swarm Optimization”. American Journal of Applied Sciences 5 (12): 1670-1675, 2008 ISSN 1546-9239.

• Szklarz M. (2010). “Principio de la Palanca en el Cuerpo Humano”. Disponible en: http://www2.ib.edu.ar/becaib//cd-ib/trabajos/Szklarz.pdf. [Consultado junio 2, 2011].

• Thompson, C y Floyd, R. (1994). “Manual of Structural Kinesiology”. Disponible en: www.fgc.edu/media/12609/biomechanics.pdf.

Otros artículos sobre Biomecánica

	Búsqueda personalizada
EFDeportes.com, Revista Digital · Año 16 · N° 160 | Buenos Aires, Septiembre de 2011 © 1997-2011 Derechos reservados