1 / 1

Introducción

    Los fisiólogos del ejercicio y del entrenamiento físico cada día se interesan más en el estudio de los cambios, modificaciones o adaptaciones de los diferentes sistemas del organismo de los deportistas y de los practicantes de actividades físicas a las cargas de entrenamiento y / o de competición.

    Se consideran dos tipos generales de adaptación. Una de origen genético, producida por mutación y recombinación de genes, y mantenida en la especie por selección natural. Y otra de origen ambiental, aquellas producidas por la norma de reacción del genotipo, variaciones de naturaleza adaptativa que sólo afectan al fenotipo y no al genotipo en sí (Berovides y Borges, 1984; Siegfried, 1988; Platonov, 1994).

    En el deporte, los estudios sobre la adaptación surgieron en la década del 70, donde se presentaron algunos modelos de adaptación a factores climatológicos (Garatinova, 1999).

    A partir de entonces, varios son los autores que coinciden en considerar que el entrenamiento deportivo es un proceso permanente de adaptación a las cargas de trabajo, con el objetivo final de mejorar las capacidades que determinan el rendimiento (Siegfried et al, 1988; Menshikov y Volkov, 1990; Rodríguez y Aragonés, 1992).

    Así, la influencia que el esfuerzo físico ejerce sobre el organismo depende de su dosificación: intensidad, número de repeticiones, carácter y tipo de ejercicio y la magnitud del descanso entre ellos (Menshikov y Volkov, 1990; Carol et al, 2002; Terjung, 2003; Negrín y Salt, 2004).

    De este modo, durante el entrenamiento deportivo el atleta recibe una carga (agente agresor o estímulo estresante), lo que le posibilitó a Seyle en 1936 proponer el concepto de Teoría del Estrés o Síndrome General de Adaptación, con sus fases de alarma, resistencia y agotamiento (Platonov, 1994; Negrín y Salt, 2004). Entre los estresores que afectan al rendimiento deportivo, y por tanto, la adaptación, deben considerarse también el cambio de horario (Alonso y Pérez, 2008), así como también los factores genéticos (Ortolano et al, 2000; Ortolano et al, 2001; Terjung, 2003; Xing et al, 2008).

    En la actualidad, gracias a la descripción de la secuencia completa del genoma humano, los estudios genéticos en el deporte han cobrado tanta importancia, que están proliferando investigaciones que intenta dilucidar la base genética de la adaptación al entrenamiento, así como el papel de este último en la prevención de enfermedades con un alto componente genético (Ortolano et al, 2000; Ortolano et al, 2001; Duchman y Berg, 2006). Algunos estudios han sido orientados a las adaptaciones producidas por el entrenamiento físico en los sistemas neural y cardiovascular (Carol et al, 2002; Huxley et al, 2008). Pero un gran número de artículos se han focalizado en las adaptaciones provocadas por el entrenamiento físico (muchas de ellas considerando el componente genético) en el consumo máximo de oxígeno (VO2 máx.) / la resistencia aeróbica (Villegas, 1991; Dionne et al, 1991; Ortolano et al, 2000; Ortolano et al, 2001; Brealy y Zhou, 2002; Xing et al, 2008). Los primeros estudios fueron los de Klissouras (1971), Klissouras (1973), Klissouras (1974), Weber et al (1976). Pero fueron Dionne et al (1991) los primeros en reportar variaciones en el ADN mitocondrial asociadas con diferencias individuales en el VO2 máx inducidos por el entrenamiento de resistencia.

    Otras adaptaciones muy estudiadas, provocadas por el entrenamiento de sobrecarga, son las del aparato neuromuscular (Villegas, 1991; Baker y Newton, 2005; Jorgensen et al, 2006; Cissik et al, 2008; Hedrick y Wada, 2008).

    El entrenamiento de sobrecarga, el denominado principio de sobrecarga o principio básico del entrenamiento de la fuerza, se ha convertido en los últimos tiempos en una práctica común, tanto para el acondicionamiento, como para la preparación de deportistas de diferentes especialidades, y para contrarrestar numerosas enfermedades de origen genético (Ortolano et al, 2000; Ortolano et al, 2001; Baker y Newton, 2005, Duchman y Berg, 2006; Hedrick y Wada, 2008; Nguyen et al, 2008; Xing et al, 2008). En este sentido, el levantamiento de pesas, donde se compite en los ejercicios clásicos de arranque y envión, constituye una de las formas típicas de entrenamiento de sobrecarga con pesos libres. Estos ejercicios y sus variantes, constituyen uno de los métodos comúnmente utilizados para el diseño de programas de entrenamientos de atletas de diferentes deportes (Hedrick y Wada, 2008).

    Una expresión integral y final de adaptación del organismo al entrenamiento deportivo, pudiera ser la edad biológica (Koladchenko, 1990) o el rendimiento deportivo (Volkov y Filin, 1989). Sin embargo, en este último sentido no tenemos noticias que éste haya sido empleado para estudiar el proceso de adaptación en el deporte, al menos en el levantamiento de pesas. Por tal motivo, el propósito de este trabajo consistió en determinar en levantadores de pesas, mediante análisis de regresión lineal simple, la respuesta adaptativa (tipos de adaptaciones) del peso relativo levantado en envión en competencias, y sus posibles relaciones con los resultados competitivos, con la finalidad de que pueda ser empleada como criterio de selección deportiva.

Muestra y metodología

    A 101 levantadores de pesas (total de la muestra) de la primera categoría participantes en la competencia nacional del año 1998, celebradas en Santiago de Cuba, cuyas características generales (edad decimal, edad deportiva y talla corporal total) y dentro de cada división del peso corporal se muestran en la tabla 1, se les recopilaron los resultados competitivos en el ejercicio de envión (fuerza absoluta máxima) logrados (durante todas sus vidas deportivas) en competencias nacionales e internacionales.

    La edad decimal se estimó siguiendo los criterios de Jordán (1977) y la edad deportiva se consideró como los años de entrenamiento en el deporte. La talla corporal total se determinó, según la técnica de estiramiento de Tanner (1964), mediante el antropómetro Harpenden (precisión ± 1 mm.).

Tabla 1. Características de la muestra estudiada. N =número de atletas, DE: desviación estándar.

Variable
División (Kg.)	N	Edad decimal (años) Media ± DE	Edad deportiva (años) Media ± DE	Talla corporal total (cm.) Media ± DE
54	12	23.201 ± 1.327	7.600 ± 3.601	153.140 ± 5.631
59	12	21.242 ± 0.690	7.411 ± 3.183	160.376 ± 3.886
64	13	22.43 ± 0.908	8.133 ± 2.899	161.850 ± 4.849
70	8	24.061 ± 1.021	9.000 ± 3.275	164.604 ± 3.464
76	16	22.620 ± 0.591	7.631 ± 2.671	168.023 ± 3.079
83	6	23.278 ± 1.394	9.166 ± 3.710	168.016 ± 2.370
91	10	23.514 ± 0.894	8.636 ± 2.766	172.945 ± 5.041
99	11	25.243 ± 1.040	10.000 ± 4.123	174.336 ± 5.066
108	6	25.096 ± 1.287	10.166 ± 3.060	177.316 ± 6.190
+ 108	7	24.213 ± 1.294	10.000 ± 4.242	179.318 ± 6.405
Total	101	23.203 ± 0.324	8.466 ± 3.317	166.213 ± 8.799

    Los resultados competitivos fueron obtenidos de los archivos de la Federación Cubana de Levantamiento de Pesas, tomados directamente en las competencias y/u obtenidos de la revista World Weightlifting (publicación oficial de la Federación Internacional de Levantamiento de pesas). Los pesos absolutos levantados en el envión fueron transformados en relativos a través de la fórmula de Malone descrita por Bale y Williams (1987), o sea, peso levantado en envión sobre peso corporal total (peso oficial de la competencia) del deportista.

    Con el objetivo de estimar el valor del intercepto (a) y de la pendiente (b) de la regresión, a cada deportista se le realizó un análisis de regresión lineal simple, del peso relativo levantado en envión (PRE) en el número de competencias para, los seis primeros resultados competitivos. Dos razones nos condujeron a la elección de un número de competencias igual a seis para los análisis de regresiones: 1. es el número mínimo de datos que se requieren para un análisis de regresión lineal simple (Sigarroa, 1985), 2. realizándose las regresiones con el mismo número de datos por atletas, se homonogeniza el efecto lineal interindividual.

    Los valores de los a y de las b de las regresiones de cada deportista, fueron promediados, por separados, dentro de cada división del peso corporal, para derivar cuatro tipos de respuestas adaptativas del PRE por los levantadores de pesas al entrenamiento y las competiciones, según los valores de los a y de las b fueran mayor o igual que el valor medio del intercepto (a media) y de la pendiente (b media), es decir, a alto (aA) y b alto (bA) respectivamente. O por el contrario, que a y b fueran menores que sus valores medios, es decir, a bajo (aB) y b bajo (bB), respectivamente. Esto fue valorado para cada atleta por separado, con respecto a los valores medios de su división del peso corporal. De esta forma, cada atleta quedó clasificado en uno de cuatro tipos de adaptaciones. Los datos fueron procesados con este fin mediante el programa de computo PSD (Fernández y Tió, 1995).

    Previamente se trató de buscar un criterio científico que permitiera un agrupamiento de las divisiones del peso corporal para estimar los valores medios de a y b. Este criterio resultó ser comparar entre divisiones del peso corporal los valores medios de los PRE (total de competencias), de los interceptos y de las regresiones.

    Los pesos absolutos levantados en envión (PAE) y los PRE se compararon entre los tipos de adaptaciones.

    Se estimaron los estadísticos de tendencia central y dispersión (media y desviación estándar), y pruebas de bondad de ajuste al test del Kolmogorov – Smirnov para cada una de las variables estudiadas. Se determinaron las asociaciones entre: a). los tipos de adaptaciones y los atletas medallistas y no medallistas, b). los tipos de adaptaciones y los lugares competitivos de los atletas.

    Los test estadísticos utilizados fueron: análisis de correlación lineal simple de Karl Pearson (entre los valores de b y a), regresión lineal simple (antes mencionada), ANOVA de un factor (efectos fijos para las comparaciones, Sigarroa, 1985), test de comparación de rangos múltiples de Duncan (como prueba post hoc) y prueba G de contingencia para las asociaciones. El paquete estadístico utilizado fue el SPSS.

Resultados

    La tabla 2 muestra los valores medios (dentro de cada división del peso corporal) de los PRE (en las seis primeras competencias), de las regresiones (b) y de los intercepto (a), así como los resultados del test de bondad de ajuste de Kolmogorov – Smirnov a la curva Gauss y Laplace para estas variables.

    Se puede apreciar que para el total de competencias, los PAE, los PRE, los valores de b y a siguieron una distribución normal al ser los valores D máx no significativos (tabla 2).

    Todos los ajustes por separados, a una ecuación lineal de regresión del PRE, por cada deportista en el número de competencias (seis) resultaron ser significativos (P < 0.05, P < 0.01 ó P < 0.001).

    Los resultados de la comparación entre divisiones del peso corporal de los valores medios de los PRE (total de competencias), de los interceptos y de las regresiones se presentan en la tabla 3.

    El ANOVA arrojó diferencias significativas (P < 0.001) entre divisiones del peso corporal con respecto al PRE; de igual forma lo hizo la prueba de rangos múltiple de Duncan (p < 0.05). Se puede observar que, no existe una separación clara y uniforme que permitiera agrupar divisiones del peso corporal sobre la base del PRE (tabla 3).

Tabla 2. Valores medios de los pesos absolutos (PAE) y relativos levantados en envión (PRE), de las regresiones (b) y 

de los interceptos de las regresiones (a) dentro de divisiones del peso corporal. N: número de atletas, NC: número de competencias totales, 

DE: desviación estándar, D máx: estadígrafo de la prueba de bondad de ajuste del test de Kolmogorov – Smirnov, ns: no significativo.

División (kg.)	N	NC	Media PAE ± DE	Media PRE ± DE	Media (b)	Media (a)
54	12	139	120.989 ± 13.120	2.307 ± 0.218	0.072	1.927
59	12	108	129.745 ± 16.733	2.268 ± 0.232	0.066	1.939
64	13	125	134.724 ± 21.359	2.220 ± 0.261	0.080	1.841
70	8	95	158.474 ± 16.435	2.369 ± 0.186	0.051	2.088
76	16	158	157.566 ± 25.219	2.200 ± 0.287	0.074	1.819
83	6	84	179.196 ± 21.544	2.284 ± 0.213	0.040	2.029
91	10	103	172.170 ± 27.358	2.045 ± 0.253	0.056	1.767
99	11	127	179.295 ± 21.614	1.994 ± 0.217	0.046	1.761
108	6	70	182.250 ± 25.242	1.807 ± 0.167	0.049	1.573
+ 108	7	88	186.108 ± 30.903	1.531 ± 0.298	0.041	1.369
Total	101	1097	157.076 ± 31.773	2.127 ± 0.331	0.059	1.825
D máx.	---	---	0.042 ns	0.037 ns	0.057 ns	0.034

 

Tabla 3. Comparación de los valores medios de los pesos relativos levantados en envión (PRE), de las regresiones (b) y de los interceptos de las regresiones (a)

 entre divisiones del peso corporal. N: número de atletas, ns: no significativo, * *: P < 0.01, ***: P < 0.001. Medias con letras en común no difieren a P > 0.05.

División (kg.)	N	Media (PRE )	Media (b)	Media (a)
54	12	2.307 ef	0.072 c	1.927 cd
59	12	2.268 de	0.066 c	1.939 cd
64	13	2.220 d	0.080 c	1.841 cde
70	8	2.369 f	0.051 c	2.088 c
76	16	2.200 b	0.074 c	1.819 de
83	6	2.284 ef	0.040 c	2.029 cd
91	10	2.045 c	0.056 c	1.767 de
99	11	1.994 c	0.046 c	1.761 de
108	6	1.807 h	0.049 c	1.573 ef
+ 108	7	1.531 g	0.041 c	1.369 f
Total	101	2.127	0.059	1.825
F	---	110.190 ***	1.650 ns	4.679 * *

    Al comparar los valores medios de b y a, el ANOVA no mostró diferencias significativas entre divisiones del peso corporal para las regresiones. Sin embargo, diferencias significativas (P < 0.01) fueron encontradas para los interceptos (tabla 3). De modo que, tampoco se observó una separación significativa clara de los interceptos, que permitiera un agrupamiento de las divisiones del peso corporal para clasificar los deportistas. Por consiguiente, fue necesario clasificar estos en uno de los cuatro tipos de adaptaciones dentro de cada división del peso corporal. Los tipos de adaptaciones derivadas por tanto fueron: aAbA, aAbB, aBbA, aBbB.

    La figura 1 muestra la representación gráfica de los tipos de adaptaciones, a través de las variaciones del PRE en un número de competencias igual a 6.

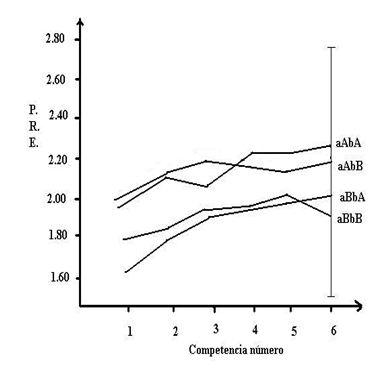
Figura 1. Variaciones del peso relativo levantado en envión con el número de competencias dentro de cada tipo de adaptación, P.R.E.: peso relativo levantado en envión,

 peso relativo medio levantado en envión en la primera competencia = 1.825, a: intercepto de la regresión, b: regresión, A: alto, B: bajo N: número de atletas. (N = 101).

    La representación de estos tipos de adaptaciones, mediante el ajuste a una ecuación lineal de regresión del peso relativo medio levantado en envión (dentro de cada tipo de adaptaciones) en el número de competencias (seis) se presenta en la figura 2.

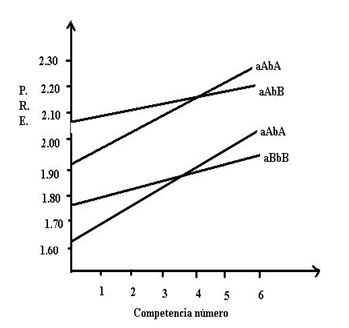
Figura 2. Representación de los tipos de adaptaciones mediante el ajuste a una ecuación lineal del peso relativo medio levantado en envión en el número de competencias, 

P.R.E.: peso relativo levantado en envión, a: intercepto de la regresión, b: regresión, A: alto, B: bajo, valor medio del intercepto de las regresiones = 1.825

    Las ecuaciones de regresión para cada tipo de adaptación resultaron ser: aAbA (1.909 + 0.073 X; r = 0.929, P < 0.01), aAbB (2.078 + 0.025 X; r = 0.867, P < 0.05), aBbA (1.622 +0.087 X; r = 0.977, P < 0.001) y aBbB (1.779 + 0.043; r = 0.866, P < 0.05), donde X es igual a número de la competencia.

    Se puede observar ahora más claramente que, sobre la base de los valores de a (A y B) y b (A y B), que estos tipos de adaptaciones pudieran interpretarse como: 1. aAbA, levantadores de pesas que inician sus vidas deportivas con altos resultados deportivos (PRE) y lo incrementan rápidamente; 2. aAbB, levantadores de pesas que inician sus vidas deportivas con altos resultados deportivos y lo incrementan lentamente; 3. aBbA, levantadores de pesas que inician sus vidas deportivas con bajos resultados deportivos y lo incrementan rápidamente y 4. aBbB, levantadores de pesas que inician sus vidas deportivas con bajos resultados deportivos y lo incrementan lentamente.

    Nótese, además, que los deportistas con los tipos de adaptaciones aAbA y aAbB en su primera competencia, en la que pudiéramos considerar que estos no poseían una "maestría deportiva" por el poco tiempo relativo que llevaban entrenando el deporte, en promedio lograron un mayor PRE que los otros atletas con los tipos de adaptaciones aBbA y aBbB, respecto al peso relativo medio levantado en envión por el total de atletas (N = 101, Figura1 y 2).

    Obsérvese que los pesistas con los tipos de adaptaciones aAbA y aAbB lograron valores medios de sus interceptos superiores al valor medio de éste al considerar la muestra como un todo (N = 101).

    Nótese también, los altos valores que relativamente presentaron las regresiones de los tipos de adaptaciones aAbA y aBbA, por lo que incrementan rápidamente el PRE con el número de competencias.

    El ANOVA y la prueba de rangos múltiples de Duncan, arrojaron diferencias significativas (P < 0.001 y P < 0.05, respectivamente) entre los tipos de adaptaciones, respecto a los valores medios de las regresiones y de los interceptos (tabla 4).

Tabla 4. Comparación de las regresiones y de los interceptos del peso relativo levantado en envión en el número de competencias entre los tipos de adaptaciones,

 a: intercepto de la regresión, b: regresión, A: alto, B: bajo, N: número de atletas, * * *: P < 0.001. Medias con letras en común no difieren a P > 0.05.

Tipo de adaptación	N	Media de las regresiones	F	Media de los interceptos	F
aAbA	12	0.072 c		1.911 c
aAbB	35	0.025 d		2.079 c
aBbA	45	0.087 c	29.013 ***	1.613 d	27.747 ***
aBbB	9	0.045 d		1.785 d
Total	101	0.060		1.825

    La tabla 5 muestra los resultados de las comparaciones del rendimiento deportivo en envión, entre los tipos de adaptaciones de levantadores de pesas. Se puede observar que, el PRE sólo difirió significativamente entre los tipos de adaptaciones aAbA y aAbB, al comparar éste en el total de competencias, siendo estadísticamente superior para el tipo de adaptación aAbA. En el resto de las comparaciones no difirieron significativamente estos tipos de adaptaciones, que se adjudicaron significativamente (P < 0.05) los valores medios más altos de los PRE.

Tabla 5. Comparación del rendimiento deportivo en envión entre los tipos de adaptaciones, a: intercepto de la regresión, b: regresión, A: alto B: bajo, 

N: número de atletas (101), NC: número de resultados competitivos, ns: no significativo, * *: P < 0.01 * * *: P < 0.001. Medias con letras en común no difieren a P > 0.05.

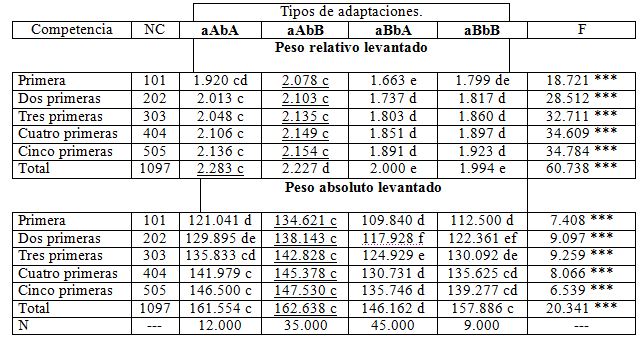
    Del mismo modo, los tipos de adaptaciones aBbA y aBbB, no difirieron significativamente (P > 0.05) en el peso relativo medio levantado en envión, en ningunas de las comparaciones efectuadas.

    Al realizar estas comparaciones respecto al peso absoluto levantado en envión, se apreció que, el tipo de adaptación aAbB, en todos los casos alcanzó mayor peso absoluto medio levantado (tabla 5).

Tabla 6. Asociación entre los tipos de adaptaciones de levantadores de pesas y el porcentaje de medallas obtenidas en competencias, 

a: intercepto de la regresión, b: regresión, A: alto, B: bajo, N: número de atletas (101), NC: número de resultados competitivos, ns: no significativo, 

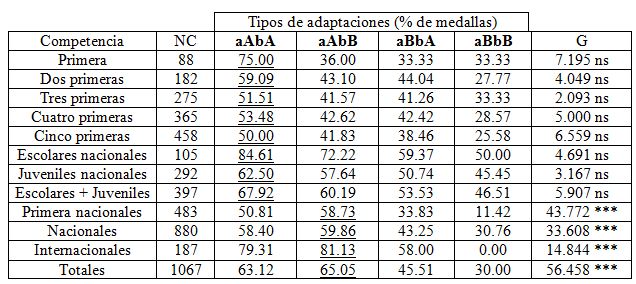
*: P < 0.05, * *: P < 0.01,*** P < 0.001. Medias con letras en común no difieren a P > 0.05.

    Al mismo tiempo, los tipos de adaptaciones aAbA y aAbB sólo difirieron significativamente, al comparar la primera y las dos primeras competencias y los tipos de adaptaciones aBbA y aBbB, en el peso absoluto medio levantado en el total de competencias; pero lógicamente como era de suponerse, en todas las comparaciones estos últimos tipos de adaptaciones promediaron menor peso medio levantado en envión.

    En la tabla 6 se puede apreciar las asociaciones entre los tipos de adaptaciones de levantadores de pesas y el porcentaje de medallas obtenidas en competencias. Aunque no se lograron asociaciones significativas, entre las variables tipos de adaptaciones y medallistas y no medallistas; desde la primera competencia (categoría escolar) hasta las competencias juveniles (sumando incluso las competencias escolares y juveniles), el mayor porcentaje de medallas fue alcanzado por los atletas con el tipo de adaptación aAbA.

Tabla 7. Asociación entre los tipos de adaptaciones de levantadores de pesas y el porcentaje de lugares obtenidos en competencias, a: intercepto de la regresión, b: regresión, 

A: alto, B: bajo, 1: medalla de oro, 2: medalla de plata, 3: medalla de bronce, N: número de atletas (101), NC: número de resultados competitivos, ns: no significativo, *: P < 0.05.

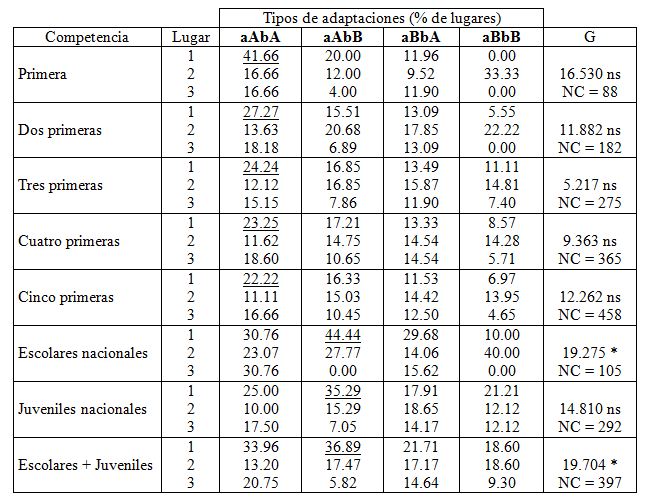
    Resultados similares se obtuvieron al asociar los tipos de adaptaciones con los lugares competitivos (10, 20, 30 y el resto de los lugares). Hasta las cinco primeras competencias el tipo de adaptación aAbA, logró los mayores porcentajes de primeros lugares (medallas de oro) en competencias; pero para el resto de las asociaciones el tipo de adaptación aAbB, se adjudicó los mayores porcentajes de primeros lugares en competencias, excepto en las competencias internacionales (tablas 7 y 7a).

    Se alcanzaron asociaciones significativas en este sentido para, las competencias: escolares nacionales (P < 0.05), totales de primera categoría (P < 0.001), nacionales totales (P < 0.001) y totales (P < 0.001, tablas 7 y 7a).

Tabla 7a. (continuación). Asociación entre los tipos de adaptaciones de levantadores de pesas y el porcentaje de lugares obtenidos en competencias, a: intercepto de la regresión b: regresión, A: alto B: bajo, 1: medalla de oro, 2: medalla de plata, 3: medalla de bronce, N: número de atletas (101), NC: número de resultados competitivos, ns: no significativo, 

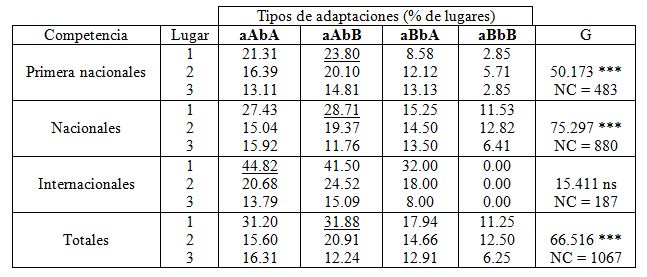
* *: P < 0.01, ***: P < 0.001.

    Se realizó un análisis de correlación lineal simple entre los valores de las regresiones (b) y de los interceptos (a), incluyendo el total de atletas de la muestra (N = 101), de tal forma que pudiera conocerse la relación entre a y b. En efecto, el resultado de este análisis fue altamente significativo (r = - 0.512, P < 0.01, N = 101, Figura 3), es decir, al aumentar a, b decreció significativamente.

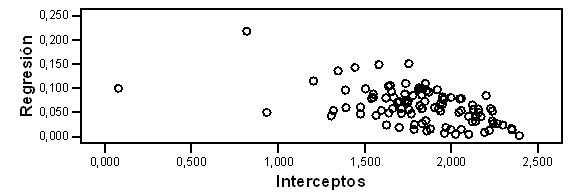
Figura 3. Análisis de correlación y diagrama de dispersión entre los valores de las regresiones (b) y de los interceptos (a). N = 101 (número de atletas), r = - 0.512 **, **: P < 0.01.

 

Tabla 8. Comparación de la edad deportiva media entre los tipos de adaptaciones. N (número de

atletas totales) = 101, n: número de atletas dentro de cada tipo de adaptación, ns: no significativo.

Tipos de adaptaciones
	aAbA	aAbB	ABbA	aBbB	F
	9.833	9.542	8.266	7.66	1.852 ns
n	12	35	45	9	---

    Al comparar la edad deportiva media entre los tipos de adaptaciones, el ANOVA no arrojó diferencias significativas entre grupos (tabla 8).

Discusión

    Al presentar los deportistas con los tipos de adaptaciones aAbA y aAbB en su primera competencia, en la que pudiéramos considerar que estos no poseían una "maestría deportiva" por el poco tiempo relativo que llevaban entrenando el deporte, un mayor PRE que los otros atletas con los tipos de adaptaciones aBbA y aBbB, respecto al peso relativo medio levantado en envión por el total de atletas (N = 101, figuras 1 y 2), nos condujo a suponer que, la influencia genética (del genotipo) sobre el PRE, pudiera estar expresada por el valor del intercepto (a, alto o bajo), pues iniciar la vida deportiva (primera competencia) con altos resultados deportivos, con poco tiempo relativo de entrenamiento (pues presentaban en promedio 13 años de edad cronológica y a penas 1 ó 2 años de entrenamiento), pudiera ser sólo explicado en este contexto, a una predisposición genética. En tanto que la influencia ambiental (tipos de entrenamientos deportivos), pudiera estar expresada por el valor de la pendiente, de la regresión (b, alta o baja).

    De ahí que, los levantadores de pesas con los tipos de adaptaciones aAbA y aAbB, tendrían ciertas ventajas sobre aquellos con los tipos de adaptaciones aBbA y aBbB, pues los primeros poseen cierta predisposición genética para realizar ejercicios de fuerza, en este caso particular, practicar el levantamiento de pesas con fines competitivos.

    Así, los pesistas con los tipos de adaptaciones aAbA y aAbB lograron valores medios de sus interceptos superiores al valor medio de éste al considerar la muestra como un todo (N = 101), lo que confirma que los atletas con los tipos de adaptaciones aAbA y aAbB, inician en promedio (comparados con los de los tipos de adaptaciones aBbA y aBbB), sus vidas deportivas con altos resultados deportivos (Figura 1 y 2, tabla 4).

    Además, debemos considerar, los altos valores que relativamente presentaron las regresiones de los tipos de adaptaciones aAbA y aBbA (tabla 4), por lo que pudiera considerarse que estos incrementan rápidamente el PRE con el número de competencias, como consecuencias del entrenamiento deportivo (del efecto ambiental).

    De este modo, a partir de las consideraciones expresadas anteriormente, era de esperar (por representar ambos, levantadores de pesas con el mismo genotipo, aA en ambientes diferentes, bA o bB), los tipos de adaptaciones aAbA y aAbB, sólo difirieran significativamente en el valor medio de las regresiones; pero no en el valor medio de los interceptos.

    Por las mismas razones, los tipos de adaptaciones aBbA y aBbB, sólo difirieron significativamente en el valor medio de las regresiones (tabla 4). Así, los tipos de adaptaciones aAbA y aAbB, pudieran considerarse fenotipos de la norma de reacción del genotipo aA y los tipos de adaptaciones aBbA y aBbB, fenotipos de la norma de reacción del genotipo aB.

    Contrario a como era de esperar, por razones que antes explicadas, el tipo de adaptación aAbA, no logró valores mayores de pesos medios levantados en envión en las comparaciones realizadas. Al mismo tiempo, teniendo en cuenta que en el levantamiento de pesas se compite por el peso absoluto levantado en envión, resultaría lógico esperar que el tipo de adaptación aAbB, alcanzara los mayores porcentajes de medallas y primeros lugares en competencias, lo que pudiera permitirnos señalar que el tipo de adaptación aAbB por el tipo de entrenamiento al que ha sido sometido, supera claramente en el éxito deportivo al tipo de adaptación aAbA, tales resultados se presentan en la tabla 6.

    Así, a partir de las competencias celebradas cuando los deportistas pasan a la primera categoría (cuando mejores resultados se esperan de ellos), hasta considerar la historia deportiva de los mismos, los mayores porcentajes de medallas fueron logrados por el tipo de adaptación aAbB (tabla 6), es decir, el tipo de adaptación aAbB, alcanzó los mayores porcentajes de medallas, en relación con el porcentaje logrado por el resto de los tipos de adaptaciones, en el total de competencias de la primera categoría (P < 0..001), internacionales totales (P < 0.001) y totales (P < 0.001).

    Resultados similares se obtuvieron al asociar los tipos de adaptaciones con los lugares competitivos (10, 20, 30 y el resto de los lugares, tablas 7 y 7ª; P < 0.001). Hasta las cinco primeras competencias el tipo de adaptación aAbA, logró los mayores porcentajes de primeros lugares (medallas de oro) en competencias; pero para el resto de las asociaciones el tipo de adaptación aAbB, se adjudicó los mayores porcentajes de primeros lugares en competencias, excepto en las competencias internacionales.

    Tratando de explicar estos hallazgos sobre un criterio científico, se realizó un análisis de correlación lineal simple entre los valores de las regresiones (b) y de los interceptos (a), incluyendo el total de atletas de la muestra (N = 101), de tal forma que pudiera conocerse la relación entre a y b (la supuesta relación genotipo - ambiente óptima). Es decir, era de esperar por los resultados encontrados con anterioridad que, al aumentar a, b disminuyera, es decir, que existiera una relación inversa entre ellos. Siendo esta al parecer, la interacción lógica y normal entre el potencial genético y la influencia ambiental en el desarrollo de la fuerza muscular (PRE), al menos en gran medida, para mantener la estabilidad y la longevidad de los altos resultados deportivos. Así, el resultado de este análisis fue altamente significativo (r = - 0.512, P < 0.01, N = 101, Figura 3), es decir, al aumentar a, b decreció significativamente. Esto pudiera explicar que en los atletas con el tipo de adaptación aAbA, se agota inapropiadamente su potencial genético ante entrenamientos "acelerados". Todo lo opuesto ocurriría en los atletas con el tipo de adaptación aAbB.

    Luego, los tipos de adaptaciones derivadas pudieran ser empleadas como criterio de selección en levantadores de pesas de la primera categoría.

    Es aceptado (Baker y Newton, 2005; Cissik et al, 2008) que las ganancias en la fuerza / potencia a medida que aumenta el estatus de entrenamiento de los sujetos se producen a una menor taza, respecto a los sujetos desentrenados o medianamente entrenados, lo que se ha explicado en la literatura científica por una mejor adaptación neural que tiene lugar durante las primeras 6 a 8 semanas de entrenamiento de fuerza, mientras que la hipertrofia tiene lugar después de este período (Tesch et al, 2004; Cissik et al, 2008). En nuestra opinión esto pudiera ser debido a que los primeros se encuentran más cerca de su potencialidad genética para la fuerza y/o potencia (más cerca de su techo genético), por cuanto el entrenamiento de sobrecarga produce ganancias en la fuerza y/o la potencia, pero el patrimonio genético establece el límite de tales ganancias. En nuestro caso, en levantadores de pesas altamente entrenados, las diferencias encontradas entre los tipos de adaptaciones (tablas 5, 6, 7, 7a) pudieran ser debidas sólo a causas genéticas y/o ambientales, pues no se encontraron diferencias significativas en las edades deportivas medias entre grupos (tabla 8).

Conclusiones

    Los análisis de regresiones lineales simples de los pesos relativos levantados en envión en el número de competencias (igual a seis), nos permitieron derivar cuatro tipos de respuestas adaptativas (tipos de adaptaciones) del peso relativo levantado en envión en levantadores de pesas (aAbA, aAbB, aBbA, aBbB), las que difirieron significativamente (P < 0.01 ó P < 0.001) en los pesos absolutos y los PRE para el total de competencias, y al mismo tiempo, éstas se asociaron significativamente (P < 0.05, P <0.01 ó P < 0.001) a los porcentajes de medallas logradas en competencias y a los lugares competitivos: 10 (medalla de oro), 20 (medalla de plata), 30 (medalla de bronce) y al resto de los lugares (a partir del cuarto lugar en adelante), por lo que se sugiere su empleo como criterio de selección en este deporte.

Referencias

• Alonso Hernández, J.R., J. Pérez González (2008): Importancia de la adaptación al cambio de horario para el rendimiento deportivo (sin fuente).

• Baker, D. and R.U. Newton (2005): Methods to Increase the Effectininess of Maximal Training for the Upper Body. Streng and Conditioning J., 27 (6): 24 – 32.

• Bale, R. y H. Williams (1987): An anthropometric prototype of female power lifters. J.Sport Med., 27: 191-196.

• Berovides Álvarez V., T. Borges Hernández (1984). Evolución. Edtl. Pueblo y Educación, Ciudad de la habana, Cuba.

• Cissik, J.M., A. Hedrick, M. Banes (2008): Challenges Applying the Research on Periodization. Strength and Conditioning J., 30 (1): 45 – 51.

• Carol, T.J, Rick and R.G. carson (2002): The Sities of Neural Adaptation Induced by Resistance Training in Human. J. Physiol., 544 (pt2): 641 – 652.

• Duchman, R.L., K. Berg (2006). The Implication of Genetic and Physical Activity on the Incidente of Osteoporosis in Pre and Postmenspausal Women. A Review. Strength and Conditioning J., 28 (2): 26 – 32.

• Dionne F., L. Tuncote, M.C. Thíbaul, M.C. Roulay, J.S. Skinner, C. Bouchard (1991): Mitocondrial DNA sequence polymorphism, VO2 máx. and reponse to endurance training. Med. Sci. Sports Exerc., 23 (2): 177-185.

• Fernández González, A., L.Tió (1997): Pronóstico y selección deportiva (PSD). Software de aplicación. Rev. Perspectiva de la Acividad Física y el Deporte. León-Castilla, España.

• Garatinova, L.G. (1991): Teoreticheskoe i iksperementalnce obosnonic tipov adaptacii V sporte. Teor. Prakt. Fiz-Kult. Edt. Fizkultura i Sport, Moskva, (7): 21-24.

• Huxley, V.H., J.J. Wang and I.H. Sarebius (2008): Adaptation of coronary microvascular exchanges in arteriales an venules to exercise training and role for sex in determining permeability responses. Am. J. Physiol. Herat Circ Physiol, 293 (2): H 1196 – NIHMS 33235.

• Häkkinen, K. et al (1998): Muscle CSA, Force Production and Activation of Leg Extensors During Isometric and Dynamic Actions in Middle – Aged and Erderly Men and Wome. J. of Aging anda Physic. Activity, 6 (3): 232 – 247.

• Hedrick, A., H. Wada (2008): Weighlifting Movements: Do the Benefits Outweigh the Risks?. Strength and Conditioning J., 30 (6). 26 – 34.

• Jorgensen, S.B., E.A. Richter and J.F.P. Wojtaszewski (2006): Role of AMPK in Skeletal Muscle Metabolim Regulation and Adaptation in Relation to Exercise. J. Physiol., 574 (pt): 17 – 31.

• Jordan, J., A. Bebelagua, M. Ruben y J. Hernández (1977): Investigación nacional sobre crecimiento y desarrollo, Cuba 1972-1974. Rev.Cub.Ped., 49 (4): 367-390.

• Komadel, L. (1988): The identification of performance potencial. En Durix, A., H.G., Knutgen y K. Tittel. The Olympic Book of Sports Medicine, vol. I of the Encyclopaedia

• Koladchenko, V.P. (1990): Metodika ppredelenija antopometricheskogo biologicheskogo rozrasta cheloveka. Teor. Prakt. Fiz Koult., (2): 35-36.

• Klissouras, V. (1971): Heretability of adaptative variation. J. Appl. Physiol., 31 (3): 338-344.

• Klissouras, V. (1974): Hérédité et entrainement. Sport Documents. Edt. E.N.S.E.P.S. París, (5): 1-12.

• Klissouras, V., F. Pirnay y J. Marie (1973): Adaptation to maximal effort: Genetic and age. J. Appl. Physiol., 35 (2): 288-293.

• Menshikov, V.V., N.I. Volkov (1990): Bioquímica. Vneshtorgizdat, Moscú.

• Nguyen, V.H., J. Loethen, T. LaFontaine (2008): Resistance Training and Dietary Supplementation for Persons UIT Reduced Bone Mineral Density. Strength and Conditioning J., 30 (5): 28 – 31.

• Negrín Pérez, R. y M. Salt Gómez (2004): Adaptación, entrenamiento deportivo y su relación con las Ciencias Biológicas. EFDeportes.com, Revista Digital. Buenos Aires. Año 10. Nº 71. http://www.efdeportes.com/efd71/adap.htm

• Ortolano, R. N. Terrados, E. Coto (2001): Marcadores genéticos relacionados con el rendimiento físico y la prevención de patologías. Arch. Med. Dep., XVIII (84). 307 – 313.

• Ortolano, R., N. Terrados, R. Álvarez, J. Rodríguez, G. Iglesias, A. cortina, E. Coto (2000): Variación Genética del Sistema Renina – Angiotensina y Deporte de Resistencia: Relación con el Rendimiento y la Prevención de Patologías. Arch. Med. Dep., XVII (80): 469 – 477.

• Platonov, V.N. (1994): La adaptación en el deporte. Segunda ed. Libergraf, S.L. Edtl. Paidotribo, Barcelona.

• Rodríguez, F.A., M.T. Aragonés (1992): Valoración funcional de la capacidad de rendimiento. En González, J.: Fisiología de la actividad física y del deporte. Edt. Interamericana / Mc Graw-Hill. Madrid, 237-278.

• Sigarroa, A. (1985): Biometría y diseño experimental. Parte I. Edt. Pueblo y Educación, 681-688.

• Sergeyevich Mishchenko, V., V. Monagorov (1995): Fisiología del deportista. Edt. Paidotribo, Barcelona España.

• Siegfried, I. (1988): Die bewegun gsbedingate koperliche adaptation añs biotisches prinzip. Theo.und Praxis der Koperkultur. Leipzig, 37 (2): 86-95.

• Tanner, J.M. (1964): "The physique of olympic athlete". London, George Allen and Unwin Ltd., 70-99.

• Vólkov, V.M., V.P. Filin (1989): Selección deportiva. Edt. Pueblo y Educación. URSS, 3-173.

• Villegas, J.A. (1991): Reconocimiento para la selección de deportistas. En Marcos, Becerro, J.F.: La Salud del Deportista, Libro I. Primera Ed. Edt. Muscle, S.A., Madrid, 29-30.

• Weber, G., A. Kartodehardjo y V. Klissouras (1976): Growth and physical training with reference to heredtity. J.Appl. Physiol., 40 (2): 211-215.

• Xing, G. Et al (2008): Adaptación and Mal – Adaptación to Ambient Hipoxia; Andean, Ethiopian an Himalaya Patterns. Plosone, 3 (6) e 2342.

Otros artículos sobre Entrenamiento deportivo

	Búsqueda personalizada
EFDeportes.com, Revista Digital · Año 16 · N° 158 | Buenos Aires, Julio de 2011   © 1997-2011 Derechos reservados