Las fórmulas estadísticas clásicas para  procesar el rendimiento técnico-táctico del voleibol The classical statistical formulas to process technical and tactical performance of volleyball
	Comisión Nacional Técnico-Metodológica de la Federación Cubana de Voleibol (Cuba)	DrC. Santiago Calero Morales scmdoctorado@yahoo.es
	Resumen           En el artículo se recopilan y describen las fórmulas estadísticas empleadas internacionalmente para procesar el rendimiento técnico-táctico del voleibol, con el objetivo de conocer particularidades de cada estructura matemática.           Palabras clave: Fórmulas estadísticas. Rendimiento técnico-táctico. Voleibol   Abstract           The article collects and describes the most used internationally statistics formulas to process the technical and tactical performance of Volleyball, with the aim of knowing specifics of each mathematical structure.           Keywords: Statistical formulas. Technical and tactical performance. Volleyball
	http://www.efdeportes.com/ Revista Digital - Buenos Aires - Año 15 - Nº 144 - Mayo de 2010

1 / 1

Introducción

    El proceso de control es por sí, expresado por uno o varios símbolos que resumen, conscientemente o no, una medida de la razón, describiendo fenómenos u objetos para determinar información útil en la optimización de la toma de decisiones.

    Los entrenadores deportivos muchas veces basan sus decisiones en situaciones de riesgo y/o incertidumbre, a partir de su conocimiento empírico, basado fundamentalmente en la experiencia y el juicio sobre hechos pasados, utilizando así una probabilidad subjetiva.

    No obstante, en la praxis resulta que muchas veces esas decisiones no se encuentran fundamentadas científicamente, por lo que son incompletas y difícilmente generalizables, provocando, por demás, errores en el proceso de estimación. Para mejorar la toma de decisiones desde el punto de vista del método científico, donde influye una amplia gama de variables, se pueden estimar las probabilidades significativas que ejerce cada variable en el rendimiento deportivo, al utilizarse, por ejemplo, ecuaciones y modelos matemáticos, conocidos en el lenguaje popular deportivo como fórmulas estadísticas.

    Una fórmula se define de forma relativa a un idioma matemático, es decir, una colección de símbolos constantes, de funciones y de relación, donde cada una de las funciones y símbolos relacionados implica Aridad¹, indicando un número de argumentos y pasos requeridos (Hinman, 2005; Wikipedia, 2009)

    En el caso específico del Voleibol, el uso de fórmulas estadísticas varía significativamente, diseñándose según la función objetivo perseguida, destacándose en esencia, las fórmulas estadísticas que estiman el rendimiento técnico-táctico del voleibolista.

    El rendimiento técnico-táctico es reconocido como un factor imprescindible (Harre, 1989; Knapp, 1963; Riera, 2000), expresándose fundamentalmente a través de las acciones técnico-tácticas representadas por el vínculo indisoluble de la biomecánica de los movimientos y la orientación táctica, conectados directamente con el resultado final (Ivoilov, 1986; Mirallas, 2001). Por ello Utkin, en Zatsiorski y col (1989) considera que dicho rendimiento está constituido por el esfuerzo realizado en la actividad deportiva en correspondencia con el resultado obtenido.

    Cada acción técnico-táctica es entendida por cada fórmula estadística como una variable de cómputo, la cual es representada a su vez por uno o varios símbolos numéricos, alfabéticos, o alfanuméricos.

    La importancia del control del rendimiento técnico-táctico, expresado en los diferentes tipos de uso que se le atribuye, supone el estudio detallado de varios aspectos que tributan directamente en el proceso de dirección del entrenamiento deportivo, tales como:

• La selección de talentos deportivos (básicamente obtenido en la etapa de máximo rendimiento deportivo).

• La exploración de contrarios.

• La promoción desde y para los medios masivos de comunicación.

    Los índices estadísticos compilados permiten elaborar índices relativos importantes para evaluar y orientar la gestión. A sus efectos, la compilación de datos provenientes de sistemas estadísticos provee a los directivos y especialistas elementos a tener en cuenta para la toma de decisiones estratégicas en los partidos (Beal, 2002); permite además un monitoreo de la actividad, la posibilidad de establecer comparaciones sobre el desempeño de lo estudiado y por ende, la corrección y aprovechamiento del suceso.

    Por ello, el diseño de cada estructura matemática debe orientarse hacia el cumplimiento efectivo y eficiente del objetivo planteado, en relación con los usos anteriormente expuestos, y además con la función específica de cada jugador (Calero, 2007a; Calero, 2007b; Calero, 2009).

    Según Callejón (2006) los primeros intentos de evaluación del rendimiento individual y colectivo del Voleibol en una competencia internacional se realizaron en la Copa del Mundo desarrollada en Alemania Oriental en 1969, y posteriormente, según Ejem y Horak (1980), se realizaron estudios de algunos aspectos metodológicos para evaluar individualidades en el Campeonato del Mundo de México 1974 y los Juegos Olímpicos de Montreal en 1976.

    No obstante, en Fiedler y col. (1974, pp. 240-241, 251-252) se evidencia la realización de estudios sobre rendimiento técnico-táctico que datan del año 1963 a 1969, así como en la década del cincuenta en la ex Unión Soviética, según consta en Zhelezniak y col. (1989, pp. 284-288).

    En Cuba se comienza a trabajar la estadística aplicada en 1964 producto de la colaboración deportiva con otros países, orientándose básicamente por el entrenador Herbert Jenter, quien proporcionó importantes conocimientos acerca del tema en una gira realizada por la Isla con el equipo nacional masculino de Alemania, además de realizar un trabajo estadístico en 1965 en partidos celebrados entre Cuba y China. Posteriormente, la influencia ejercida por los alemanes con los modelos estadísticos utilizados en la planificación deportiva, denominados “Factores de Rendimiento”, básicamente implantada por Dieter Ground (Poyato, 1969), sentó las bases del desarrollo de esta disciplina en el país (Perdomo, 1983).

    La fórmula estadística evolucionó con gran fuerza en el Voleibol moderno, diseñándose la mayoría de ellas en la década del sesenta, según consta en los estudios referenciales (Calero 2007a). Sin embargo, la aplicación práctica a gran escala de cada fórmula estadística dependió más del desarrollo tecnológico que de las necesidades del entrenador acerca de utilizar modelos confiables que evaluaran particularidades individuales y colectivas en el Voleibol. Se considera que esto se debe a que el desarrollo informático elevó considerablemente la cantidad, almacenamiento y calidad del registro y procesamiento de la información (Morante y Villa, 2002).

    Con anterioridad a la etapa actual de alto desarrollo tecnológico, la objetividad en el registro, y sobre todo en el procesamiento de la información, era la premisa fundamental a tener en cuenta en la aplicación de ecuaciones y modelos matemático- estadísticos que conforman las distintas fórmulas de estimación del rendimiento técnico-táctico del voleibolista, y que entre otros aspectos fue representativo del diseño de sistemas estadísticos simplificados, tales como el Más-Menos (Perdomo, 1983).

    En el presente trabajo se describen las fórmulas matemáticas que a lo largo de la historia del Voleibol han sido, y son, las más empleadas internacionalmente. La recopilación bibliográfica realizada permite organizar las herramientas matemáticas creadas y utilizadas por diferentes autores, conociendo de esa forma las particularidades esenciales de cada fórmula, sus potencialidades y limitantes, así como trazar estrategias eficientes para su implementación presente y futura.

Metodología

    Las variables que procesa cada fórmula estadística son registradas por diversas metodologías observacionales, las que plasman en protocolos específicos, a través de criterios, las distintas acciones técnico-tácticas ejecutadas. A continuación se muestra un ejemplo para cuantificar el significado de cada variable procesada, en este caso la metodología de Jim Coleman (Schleuder S. y Franco-Reed, 2002), la cual fue traducida y modificada para una mejor comprensión, tomándose el símbolo “A” como sinónimo de Acción técnico-táctica:

• 4 puntos para un saque punto (A+ o A4): Ocurre cuanto el saque obtiene el punto haciendo contacto con el terreno oponente o los jugadores al recibo no pueden mantener el balón debido a la dificultad con que se recibió el balón.

• 3 puntos para un saque al cual el armador no llega y otro jugador arma (A* o A3): Se obtiene cuando el saque le imposibilita al contrario armar una ofensiva; generalmente se entrega el balón o el mismo viaja de forma directa al terreno del sacador.

• 2 puntos para un saque con el cual el armador no puede jugar por el centro (A0 o A2): El saque le permite al recibo enviar el balón a zonas óptimas para ser pasado hacia el atacador, omitiendo solamente las combinaciones con el jugador central.

• 1 punto para un saque que es recibido perfectamente, posibilitándole al armador cualquier opción de ataque (A/ o A1): El saque le permite al recibo enviar el balón a zonas óptimas para ser pasado con sistema de juego rápido, permitiendo además todas las combinaciones posibles con el pasador (Zona 3x2).

• 0 punto por un error de saque (A- o A0): El saque es contra la net, fuera, o es penalizado por el árbitro al cometerse falta técnica.

Desarrollo

    La clasificación de cada fórmula estadística requiere de un estudio a partir de la distinción de dos grupos. El primero de ellos, conformado por aquellas que emplea la Federación Internacional de Voleibol (FIIVB), (se prioriza su análisis pues esta es la institución rectora del Voleibol y a través de ellas se seleccionan los mejores jugadores de los campeonatos internacionales y nacionales de numerosos países, entre otros aspectos), con una finalidad eminentemente comercial. El segundo grupo está conformado por aquellas fórmulas diseñadas en diferentes etapas por instituciones dedicadas a la investigación en el área deportiva, específicamente del Voleibol, con un carácter eminentemente pedagógico.

    Atendiendo a la importancia de las variables que presenta el cómputo numérico en cada fórmula estadística, estas pueden clasificarse en dos tipos. Las “Variables influyentes” son las que se relacionan directamente con el rendimiento técnico-táctico individual, influyendo directamente sobre el marcador del partido. Las “Variables Secundarias” son aquellas relacionadas con el rendimiento colectivo del equipo, así como constantes añadidas según lo propuesto por cada autor.

    Tanto las ecuaciones como los modelos matemáticos que conforman cada fórmula estadística pueden clasificarse según la cantidad de variables influyentes en su cómputo, definiéndose como:

• Fórmulas de una variable influyente

• Fórmulas de dos variables influyentes

• Fórmulas de tres variables influyentes

• Fórmulas de cuatro o más variables influyentes

    Las fórmulas más utilizadas de una variable fundamental, son las siguientes:

Donde: La Fórmula 1.1 obtiene el Average² (Av) de: j (jugador); A= Acciones técnico-tácticas; Tn=Técnica escogida; Jg=Juegos realizados; e=Equipo.

Fuente: Sydex Volleyball Stats, 2002; StatTrak For Volleyball 6.01, 1998 y VBSTATS32 versión 3.2.0E, 2002; 

League Analyzer for Volleyball v3.2.0, 2005; Volleyball Statware v6, 2006; Quality Stats Volleyball V10.1.0, 2010

Donde: La Fórmula 1.2 obtiene el Average (Av) de: j (jugador); A= Acciones técnico-tácticas; Tn=Técnica escogida; Ts= Sets realizados; e=Equipo.

Fuente: (FIVB, 2003)

    La fórmula o Ecuación 1.1 se utiliza para evaluar individualmente un voleibolista en todos los fundamentos técnico-tácticos, mientras que la fórmula 1.2 es aplicada por la FIVB para determinar el Mejor Jugador en los fundamentos de Saque, Pase, Defensa y Bloqueo.

    Estas fórmulas poseen como característica común un fácil cómputo, y por ende su procesamiento se hace económico para contextos con escasa infraestructura tecnológica y de recursos humanos.

    Para mayor comprensión de su procesamiento en la Tabla 1.1 se ejemplifica hipotéticamente el rendimiento de dos jugadores por partido y sets.

Tabla 1.1. Ejemplo del procesamiento estadístico de las fórmulas 1.1 y 1.2

Jugador	Set 1	Set 2	Set 3	Set 4	Set 5	Sets jugados	Total puntos (A+)	Fórmula 1.1	Fórmula 1.2
A	6	7	5			3	18	18 a/j	6 a/sets
B	4	3	3	4	4	5	18	18 a/j	3.6 a/sets

Fuente: Elaboración propia

    Atendiendo a que la Fórmula estadística 1.1 divide el total de puntos obtenidos en el Saque entre el Total de Juegos donde participa cada jugador, tanto el voleibolista A como el B se encuentran empatados en su rendimiento (18 a/j: 18 puntos de average por juego). Mientras que en la Fórmula 1.2, se obtiene el Total de Puntos (en el numerador) dividido por el total de sets jugados por el equipo, estimándose que el jugador A posee más rendimiento que el jugador B. (6 a/sets³ y 3.6 a/sets respectivamente).

    Las fórmulas más utilizadas que incluyen dos variables fundamentales, son las siguientes:

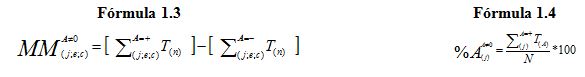
Donde: La Fórmula.1.3 obtiene el índice Más-Menos (MM) de: j (jugador); e=Equipo; c=Campeonato de A= Acciones técnico-tácticas; Tn=Técnica escogida.

Fuente: (Perdomo, 1983; Santana., 1989 y Navelo., 2004)

Donde: La Fórmula 1.4 obtiene el Por Ciento de la Acción (%A) de: j= Jugador; en A= Acciones técnico-tácticas; Ta=Técnica Ataque; N=total de Observaciones.

Fuente: (Fiedler., 1974, p. 240-241, 243; Díaz, 1997; VBSTATS32 VERSION 3.2.0e, 2002; Copello, 2003; TurboStast for Volleyball V2, 2004; DataVolley 2, 2005 

y DataVolley 2007 Pro; Fernández, 2005; VolleySoft MultiPasport, 2005; FIVB, 2003; Ace Volleyball Analyzer v7, 2009; Quality Stats Volleyball V10.1.0, 2010)

    La Fórmula 1.3 representa el llamado Sistema Más-Menos, de gran difusión en Cuba, utiliza las dos variables más importantes del rendimiento individual. Por otra parte, la Fórmula 1.4, muy empleada internacionalmente, procesa dos variables del rendimiento, la de máxima evaluación en el numerador, y el total obtenido en el denominador, donde se incluyen las variables conocidas como Intentos, así como aquellas que provocan la pérdida inmediata del punto; aplicadas por la FIVB para seleccionar el Mejor Jugador en el Ataque y el Mejor Libero del Campeonato.

    Para una mejor comprensión de su procesamiento en la Tabla 1.2 se ejemplifica hipotéticamente el rendimiento de dos jugadores en cada partido.

Tabla 1.2. Ejemplo del procesamiento estadístico de las fórmulas 1.3 y 1.4

JUGADOR	Variable 4 (A+)	Variable 0 (A-)	TOTAL ACCIONES	Fórmula 1.3	Fórmula 1.4
A	5	5	10	0	50%
B	5		5	+5	100%

Fuente: Elaboración propia

    La Fórmula 1.3 (Más-Menos) resta las variables de evaluación “Cuatro” con los “Ceros”, o sea, son antagónicas. El jugador A posee un rendimiento de Cero, mientras que el jugador B posee un índice de +5 (5-5=0; 5-0=5 respectivamente). Para el caso del procesamiento de la Fórmula 1.4 (Es una frecuencia porcentual; por lo cual suma el total de variables de interés como parte de numerador y las divide por el total de observaciones, multiplicando posteriormente por cien), el jugador A es inferior en rendimiento que el jugador B (50% y 100% respectivamente).

    Al igual que las fórmulas que procesan una variable fundamental, estas se caracterizan por un fácil cómputo, aspecto que tributa a una mayor objetividad en cuanto a otros modelos estadísticos que procesan más variables, sobre todo cuando existen pocos recursos tecnológicos y de recursos humanos.

    Las fórmulas de tres variables fundamentales más utilizadas son las siguientes:

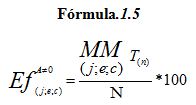
Donde: La Fórmula 1.5 obtiene la Efectividad (Ef) de: j= Jugador; e= Equipo; c= Campeonato de A= Acciones técnico-tácticas; 

MM= Índice Más-Menos (Ecuación 1.3) de Tn=Técnica Escogida en N= Total de Observaciones.

Fuente: (StatTrak for Volleyball, v6.01, 1998; VBSTATS32 V3.2.0E, 2002; FIVB, 2003 VolleySoft MultiPasport, 2005; Oliveira y col., 2005; Mesquita. y col., 2001⁴ ;

 Sydex Volleyball Stats, 2002; League Analyzer for Volleyball v3.2.0, 2005; Volleyball Statware v6, 2006; Quality Stats Volleyball V10.1.0, 2010)

 

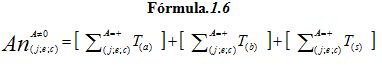
Donde: La Fórmula 1.6 obtiene el Máximo Anotador (An) de: j= Jugador; e= Equipo; c= Campeonato de 

A= Acciones técnico-tácticas; de Ta=Técnica Ataque; Tb=Técnica Bloqueo; Ts=Técnica Saque.

Fuente: (FIVB, 2003)

    La Fórmula 1.5 es muy empleada en Cuba y una de las más utilizadas en el mundo, debido a su importancia integradora (Calero, 2007b). La Fórmula 1.6 es aplicada por la FIVB para determinar el “Máximo Anotador”, construida con la suma de las acciones de máxima evaluación de fundamentos ofensivos, las cuales provocan puntos absolutos en el marcador del juego.

    Las fórmulas que procesan tres variables influyentes permiten un índice de confiabilidad superior que aquellas fórmulas que solo procesan una o dos variables significativamente influyentes en el rendimiento técnico-táctico (Calero, 2009). Estos tipos de modelos necesitan un mayor volumen de recursos tecnológicos y humanos, debido a su nivel superior de especialización.

    Para una mejor comprensión de su procesamiento en la Tabla 1.3 se ejemplifica hipotéticamente el rendimiento de dos jugadores.

Tabla 1.3. Ejemplo del procesamiento estadístico de las fórmulas 1.5 y 1.6

JUGADOR	Variable 4 (A+)	Variable 3 (A-)	Variable 1 (A/)	TOTAL ACCIONES	Fórmula 1.5	Fórmula 1.6
A	5	2	10	17	17.65%	5
B	5	2	5	12	25%	5

Fuente: Elaboración propia

    La Fórmula 1.5 presenta en su numerador el modelo estadístico del sistema Más-Menos (Fórmula 1.3), por lo que su procedimiento ha sido explicado anteriormente. El cómputo final del numerador es dividido por el total de acciones obtenidas por los jugadores (17 y 12 respectivamente), multiplicando el valor obtenido por cien. Lo anterior alcanza una unidad de medida en por cientos, obteniendo el jugador A menor rendimiento que el jugador B (17.65% y 25% respectivamente).

    Para el caso de la Fórmula 1.6, el procesamiento es más sencillo, pues este modelo estadístico obtiene la sumatoria de los puntos obtenidos en los fundamentos ofensivos (Ataque, Saque y Bloqueo), por ello se determina el Máximo Anotador de un partido o campeonato (FIVB, 2003). Para el caso, al presentarse solo las variables del fundamento Saque, ambos jugadores poseen la misma cantidad de puntos (5 puntos).

    Las fórmulas de cuatro variables o más están representadas por los siguientes modelos estadísticos:

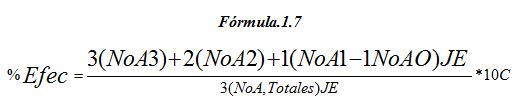
Donde: La Fórmula 1.7 obtiene el por ciento de Efectividad (%Efec) de: j= Jugador; e= Equipo; c= Campeonato de A= Acciones técnico-tácticas; NoA3= Acciones evaluadas de Tres Puntos; NoA2= Acciones evaluadas de Dos Puntos; NoA1= Acciones evaluadas de Un Punto; NoA0= Acciones evaluadas de Cero Puntos; NoA, Totales= Totales de Acciones Observadas.

Fuente: (Álvarez, 2001. p. 118). También se puede consultar una Fórmula de estructura similar en: (Díaz, 1997; Molina y Barriopedro, 2000; Molina y col, 2004)

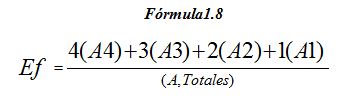
Donde: La Fórmula 1.8 obtiene la Eficiencia (Ef) de: j= Jugador; e= Equipo; c= Campeonato de A= Acciones técnico-tácticas; A4= Acciones evaluadas de Cuatro Puntos; 

A3= Acciones evaluadas de Tres Puntos; A2= Acciones evaluadas de Dos Puntos; A1= Acciones evaluadas de Un Punto; A, Totales= Totales de Acciones Observadas.

Fuente: Jim Coleman en: Schleuder S. y Franco-Reed D, 2002. Otras fórmulas se encuentran disponibles en: (Dieter Ground en: Poyato, 1969; Fiedler y col., 1974; Díaz, 1997; 

Mesquita. y col., 2001; VBSTATS32 V3.2.0E, 2002; VolleySoft MultiPasport 2005; DataVolley 2, 2005 y DataVolley 2007 Profesional, 2007⁵; Volleyball Coach v10.11, 2008; 

Quality Stats Volleyball V10.1.0, 2010)

    Para una mayor comprensión en la Tabla 1.4 se ejemplifica hipotéticamente el rendimiento de dos jugadores.

Tabla 1.3. Ejemplo del procesamiento estadístico de las fórmulas 1.7 y 1.8

jugador	Variable 4 (A+)	Variable 3 (A*)	Variable 2 (A0)	Variable 1 (A/)	Variable 0 (A-)	total	Ecuación 1.7	Ecuación 1.8
A	1			1	1	3	@3.333	1.67 ptos
B	1		2		1	4	@5.000	2 ptos

Fuente: Elaboración propia⁶

    La Fórmula 1.7, que es una modificación de la Fórmula 1.8 (Calero 2007a), determina el rendimiento técnico-táctico basado en valores numéricos que multiplican las variables. Estos valores, presentes en ambas fórmulas, multiplican la cantidad de variables en el numerador, siendo los múltiplos mayores a medida que las variables son más importantes. Ambas fórmulas posteriormente son divididas por la cantidad total de acciones, aunque la Fórmula 1.7 multiplica ese total por el valor máximo que alcanzan las variables (3 puntos) como aspecto diferente.

    La Fórmula 1.7, y sobre todo la 1.8 son las más utilizadas internacionalmente para procesar profesionalmente el rendimiento técnico-táctico del voleibolista. Su implementación necesita en términos prácticos un volumen tecnológico y de personal especializado mucho mayor que el resto de los modelos estadísticos, debido a la complejidad de su procesamiento y a la cantidad de variables que modela. Su nivel de exactitud es muy superior (en términos de probabilidades, y de integralidad) que el resto de las fórmulas enunciadas con posterioridad. No obstante, estas no están sujetas a errores de estimación, provocados por diversos problemas o anomalías matemáticas que presentan, las cuales son demostradas y corregidas en Calero, 2009.

    Internacionalmente existen de por sí otro número de fórmulas encargadas de procesar las variables del rendimiento técnico-táctico del voleibol, la mayor parte disponible en Díaz (Díaz, 1997), así como en Ivoilov y Poyato (Ivoilov, 1986, Poyato, 1969). No obstante, su estudio no resulta significativo pues algunas han perdido vigencia en la práctica y otras son simples modificaciones de las anteriormente referenciadas.

    Las características generales de las fórmulas recopiladas denotan una alta variedad de criterios y aplicación práctica, por lo que su interpretación e implementación estará sujeta al razonamiento detallado de sus componentes y al objetivo perseguido por el analista, aspecto esencial para valorar sus cualidades como interpretación reducida de la realidad.

Conclusiones

    De forma general podemos concluir que:

1. Las fórmulas clásicas utilizadas internacionalmente para procesar el rendimiento técnico-táctico del voleibolista son ocho, las que se diferencian básicamente por la cantidad de variables empleadas en su cómputo.

2. Los criterios actuales para el diseño de fórmulas estadísticas varían significativamente, estando sujeta su aplicación al objetivo perseguido y las posibilidades de aplicación práctica.

Notas

1. La Aridad desde el punto de vista matemático está definida como un operador matemático para calcular una función determinada. Ejemplo: la Suma “+” y la Resta “-”.

2. Average, palabra de la lengua inglesa, es utilizada en el deporte como sinónimo de promedio de cálculo, especificando una medida del rendimiento deportivo basada en normas previamente establecidas (Encarta, 2009)

3. Se entiende a/sets por average por sets.

4. No todos los autores tienen la misma organización de la fórmula anterior, aunque en estructura son similares.

5. La fórmula mostrada pertenece a los primeros autores, estos utilizan una escala de 5 criterios en el Saque. Ecuaciones similares se aprecian en las referencias posteriores. El DataVolley2, 2005, Pág.44, incluye una multiplicación de un exponente libremente escogido. La reproducción de las ecuaciones 1.7 y 1.8 es exacta a las originales de sus respectivos autores.

6. Tanto en la Ecuación 1.7 como la 1.8 se utilizan otros símbolos para mostrar las variables. No obstante, se seleccionaron los símbolos comunes más utilizados en Cuba, enumerándose de izquierda a derecha según su nivel de importancia y la influencia positiva que ejercen en el rendimiento.

Referencias bibliográficas

• Ace Volleyball Analyzer v7. (2009). Dimensional Software Inc. USA

• Álvarez J. (2001). De la Cancha a la Arena. Real Federación Española de Voleibol. pp. 115-118

• Beal, D. (2002). Sistemas y Tácticas Básicas de Equipo. Manual del Entrenador de Voleibol, Nivel 1. Capítulo 15. Lausanne, FIVB. Impartido en Esplugues de Llobregat, Barcelona, España. Del 1 al 12 de agosto de 2002 (Versión Electrónica). Real Federación Española de Voleibol (RFEVB).

• Calero S. (2009). Sistema de registro y procesamiento del rendimiento técnico-táctico para el voleibol de alto nivel. Tesis en opción al grado científico de doctor en Ciencias de la Cultura Física. Departamento de Juegos Deportivos. Universidad de Ciencias de la Cultura Física y el Deporte “Manuel Fajardo”. La Habana. Cuba.

• Calero, S. (2007a). Diseño de modelos matemático estadísticos para procesar rendimiento en los voleibolistas. I Curso Nacional sobre control del rendimiento en Voleibol y Voleibol Playa. Escuela Nacional de Voleibol y Escuela Internacional de Educación Física y Deportes (EIEFD), del 26 de mayo al 2 de junio del 2007. La Habana, Cuba.

• Calero, S. (2007b). Los modelos matemáticos C, para procesar rendimiento en los voleibolistas. VI Conferencia Internacional Científico Pedagógica de Cultura Física y Deportes. Revista Digital “PODIUM” Facultad de Cultura Física “Nancy Uranga Romagoza” Pinar del Río, Número 2148-Abril 2007.

• Callejón, D. (2006). Estudio y análisis de la participación técnico-táctica del jugador Líbero en el Voleibol masculino de alto rendimiento. Tesis doctoral del Departamento de Física e Instalaciones Aplicadas a la Edificación, al Medio Ambiente y al Urbanismo. Escuela Superior de Arquitectura. Madrid, España, pp.361-264.

• Copello, M. (2003). El Judo: control del rendimiento táctico. EFDeportes.com, Revista Digital. Buenos Aires, Año 9, N° 60, Mayo. http://www.efdeportes.com/efd60/judo.htm

• DataVolley 2 (2005). Manuale Data Volley Lite. Version Release 2.1.2.

• DataVolley 2007 Profesional (2007). HandBooks. Software for the scouting and analysis of Volleyball matches. Created and distributed by: DataProject, sport software. Bologna. Italia, pp.16

• Díaz, J. (1997). Voleibol, La dirección de equipos. Métodos estadísticos y evaluación competitiva. Editorial Deportiva Wanceulen, Sevilla, España. pp. 113-164

• Ejem, M. y Horak, J. (1980). Selected findings from statistical analisis of individual play in Czehoslavak Championships. Volleyball Technical Journal. Noviembre, Canadian Volleyball Association. Canada pp. 3-17

• Encarta, (2009). 1993-2008 Microsoft Corporation. USA

• Fernández, M. (2005). Efecto de la aplicación de un sistema automatizado de proyección de preíndices en la mejora de la efectividad de la acción de Bloqueo en voleibol, Tesis doctoral. Editorial de la Universidad de Granada. España. pp. 171

• FIVB (2003) CD-ROM- Top Volley: El juego masculino: Técnica y Táctica. Lausana. Suiza.

• Harre, D. (1989). Teoría del Entrenamiento Deportivo. Editorial Científico Técnica, La Habana, Cuba, pp. 314-363; 18

• Hinman, P. (2005). Fundamentals of Mathematical Logic. Tronconal: A K Peters, pp.153

• Ivoilov, A. (1986). Voleibol: Técnica-Táctica-Entrenamiento. Editorial Estadium, Buenos Aires, Argentina. pp. 2, 23.

• Knapp, B. (1963). Skill in sport: the attainment of proficiency. Routledge and Kegan Paul, Londres. England.

• League Analyzer for Volleyball v3.2.0 (2005). Analyser Software Inc. USA

• Mesquita, I. y col (2001). A relação entre a eficiência e a eficácia no domínio das habilidades técnicas em Voleibol. Revista Portuguesa de Ciências do Desporto, vol. 1, nº 3. Faculdade de Ciências do Desporto e de Educação Física Universidade do Porto. Portugal. pp.33-39

• Mirallas, J.A (2001). La Acción técnico-táctica en el judo. Universidad de Ciencias del Deporte. Departamento de Planificación. Barcelona, España. pp.23

• Molina, J.J y Barriopedro, M.I (2000). Análisis de le relación entre el rendimiento del saque de voleibol y los factores contextuales. Universidad Europea de Madrid. España.

• Molina, J.J y col (2004). Análisis de juego desde el modelo competitivo: Un ejemplo aplicado al Saque en Voleibol. Revista Kronos No 5-enero-julio. Universidad Europea de Madrid. España. pp.38

• Morante, J.C.; Villa, J.G. (2002). Valoración técnico-táctica y control del entrenamiento a través de programas informáticos. Rendimiento Deportivo, N°1.

• Navelo, R.M (2004). El joven voleibolista. Editorial José Martí. La Habana. Cuba. pp. 63-67

• Oliveira, R. y col (2005). Caracterização da eficácia do bloco no Voleibol de elevado rendimento competitivo. Estudo aplicado em equipas masculinas participantes na Liga Mundial 2003. EFDeportes.com, Revista Digital. Buenos Aires, Año 10, N° 84, Mayo. http://www.efdeportes.com/efd84/voleibol.htm

• Perdomo, A. (1983). Método estadístico Mas- Menos (+ -). Tesis de Diplomante. Instituto Superior de Cultura Física “Manuel Fajardo”, La Habana. Cuba.

• Poyato, N.J. (1969). Apuntes sobre las estadísticas alemanas de 1969 impartidas en Cuba por Dieter Ground. Federación Cubana de Voleibol (inédito).

• Quality Stats Volleyball V10.1.0 (2010).

• Riera, J. (2000). Fundamentos del aprendizaje de la técnica y la táctica deportivas. Editorial INDE, Barcelona, España, pp.38-41.

• Santana, J. (1989). Análisis del rendimiento técnico-táctico de los voleibolistas mediante el método estadístico Más (+) Menos (-), Revista Actualidad Deportiva No. 1 de 1989. Facultad de Cultura Física “Manuel Fajardo”, Villa Clara, Cuba.

• Schleuder, S. y Franco-Reed, D. (2002).”Este Saque es para Ud.” Los elementos básicos del juego. Capitulo 7. Editado por la Asociación de entrenadores de Voleibol de los EE.UU, pp.39-41.

• StatTrak for Volleyball, v6.01 (1998). All-Pro Software Inc., Madison. USA

• Sydex Volleyball Stats (2002). Sydex Computer System. Designer and produced by: Michael Phillips & Melanie Bolt. USA.

• TurboStast for Volleyball V2(2004). TurboStast Software Company. Po Box, Towaco, NJ. USA.

• VBSTATS32 V3.2.0e (2002). Park Enterprises, Nebraska, USA.

• Volleyball Coach v10.11 (2008). All Stats Software, Santa Rosa, California, USA

• Volleyball Statware v6 (2006). Team Statware Statistics software for Volleyball User Manual. Digital Scout. West Henderson Road Columbus. USA.

• VolleySoft MultiPasport (2005). Guía del Usuario. Francia. http://perso.wanadoo.fr/caribean.voleibol/page3.htm

• Zatsiorski, V. y col.(1989). Metrología Deportiva. Editorial Planeta, Moscú. URSS.pp.178-214

• Zhelezniak, Y. y col (1989). La preparación de los Voleibolistas jóvenes.; Editorial Científico Técnica. La Habana; Cuba. pp. 284-286

Otros artículos sobre Voleibol

	Búsqueda personalizada
revista digital · Año 15 · N° 144 | Buenos Aires, Mayo de 2010   © 1997-2010 Derechos reservados