
|
|||
|---|---|---|---|
|
|
Orientaciones de carácter metodológico para el uso del análisis factorial en el deporte |
|
|
|
*Doctora en Ciencias de la Cultura Física Profesora Titular de Métodos de Análisis e Investigación. Máster en Matemática Aplicada Metodóloga para la Formación Doctoral en la Facultad de Villa Clara del Instituto Superior de Cultura Física “Manuel Fajardo” Vice coordinadora del programa doctoral curricular colaborativo en Ciencias de la Cultura Física (Especialidad Deporte) Miembro del Tribunal Permanente del Grado de Doctor en Ciencias de la Cultura Física en Cuba ** Doctor en Ciencias de la Cultura Física Metodólogo integral de Deporte de Alto Rendimiento del Sectorial Provincial del Instituto Nacional de Deportes, Educación Física y Recreación en Villa Clara Profesor asistente de la Facultad de Villa Clara del Instituto Superior de Cultura Física “Manuel Fajardo” Colaborador de la Comisión Nacional de Tiro Deportivo |
Dra.C. Magda Mesa Anoceto* Dr.C. Rodolfo Vidaurreta Bueno** (Cuba) |
|
|
|
Resumen La investigación en el deporte tiene que afrontar con frecuencia la recogida de datos acerca de múltiples variables que intervienen en sus procesos. El estudio de dichos datos por medio de técnicas de análisis multivariante, tanto en el enfoque exploratorio como confirmatorio, se revela como imprescindible para comprender adecuadamente el funcionamiento de dichos procesos. El objetivo de este trabajo consiste en orientar metodológicamente el uso del análisis factorial como técnica multivariada en las investigaciones del deporte para de esta manera facilitarles a los interesados una herramienta para su uso sin exigir amplios conocimientos estadísticos matemáticos. Palabras clave: Análisis factorial. Deporte. Investigación |
|||
|
|
http://www.efdeportes.com/ Revista Digital - Buenos Aires - Año 14 - Nº 134 - Julio de 2009 |
|
|
1 / 1
Introducción
Se sabe que la investigación en el deporte tiene que afrontar con frecuencia la recogida de datos acerca de múltiples variables que intervienen en sus procesos. El estudio de dichos datos por medio de técnicas de análisis multivariado tanto en el enfoque exploratorio como confirmatorio, se revela como imprescindible para comprender adecuadamente el funcionamiento de dichos procesos.
Sin embargo, se ha constatado en estudios realizado por Mesa (2001, 2006) que hay un sobreuso de técnicas estadísticas univariadas en la investigación del deporte, en detrimento del uso de técnicas multivariadas, o una combinación de ellas.
La utilización de una serie de análisis univariados para cada una de las variables en estudio, por lo general, no es lo adecuado, ya que se ignoran las correlaciones entre las variables y así se puede, en algunas ocasiones, falsear los resultados. Por otra parte, el análisis multivariado puede arrojar luz sobre relaciones, independencia relativa de las características consideradas y dar más información objetiva. Muchas son las investigaciones en el deporte que requieren del análisis multivariado.
Entre las técnicas estadísticas que pueden emplearse con un enfoque exploratorio y un enfoque confirmatorio está el análisis factorial.
Si bien los planteamientos iniciales del análisis factorial fueron obra de los matemáticos, fueron los psicólogos quienes le dieron una aplicación práctica. Posteriormente, el análisis factorial se ha aplicado en diversas áreas de conocimiento; el deporte es una de ellas.
La difusión del análisis factorial fue impulsada, a partir de la década de 1960, por la irrupción de cada vez más potentes equipos de cómputo así como por el desarrollo de programas informáticos cada vez más accesibles como el SPSS.
En el contexto, determinado por el panorama descrito anteriormente y la necesidad de que la estadística se use como instrumento de investigación y no como producto final de la misma, surge la idea de ofrecer orientaciones metodológicas para el uso del análisis factorial como técnica multivariada en las investigaciones del deporte sin exigir amplios conocimientos estadísticos matemáticos por parte de los interesados.
El trabajo da respuesta a las siguientes interrogantes: ¿Qué es el análisis factorial? ¿Cuándo se utiliza? ¿Cómo se aplica? Se presenta un ejemplo práctico utilizando el SPSS y se hace referencias a otras situaciones que ejemplifican su utilidad en el deporte.
Desarrollo
Respuesta al ¿Qué es?
El análisis factorial es una técnica estadística cuyo objetivo esencial es reducir el conjunto de datos aportados por m variables X1, X2..., Xn suficientemente bien correlacionadas, a unos pocos factores F1, F2..., Fp que sean capaces de explicar en gran medida, la variabilidad de la muestra original.
Existen varios métodos de extracción de los factores, el más conocido de ellos es el método de componentes principales. Este analiza tablas rectangulares de datos, en las que las columnas representan las variables y las filas a los individuos.
Respuesta al ¿Cuándo se utiliza?
Mesa (2006: 75) plantea que “…la validez de un análisis de factor está condicionada por la existencia de correlaciones integrales y suficientemente buenas entre las variables originales, mientras que su éxito depende, en buena medida de la naturaleza de la investigación y de la simplificación que se logre de la variabilidad reproducida…”.
El análisis factorial se usa especialmente con fines exploratorios, para detectar la existencia de posibles componentes subyacentes o denominaciones fundamentales en el fenómeno que permiten descubrir nuevos conceptos y reducir los datos. En resumen, simplifica y organiza en estructuras más generales un gran número de variables.
Los objetivos que llevan a un investigador a utilizar el análisis factorial son diversos:
tener medidas de un conjunto de variables, y después de conocidas realizar la construcción relacional subyacente entre las variables, a fin de explicar dichas influencias;
probar una hipótesis de trabajo sobre el número y la naturaleza de las construcciones factoriales que explican las relaciones entre variables;
desear simplemente una reducción de datos;
problemas relacionados con la búsqueda de un indicador.
Desde luego, el principal objetivo de análisis factorial es la agrupación de variables, donde, dado un conjunto de n variables sobre N individuos, se quiere obtener un conjunto más reducido m de componentes latentes (no observables) que expliquen la covarianza existente entre las n variables, con la condición de que:
m sea pequeño,
se pierda el mínimo posible de información,
la solución obtenida sea fácilmente interpretable.
Respuesta a ¿Cómo se aplica?
Pasos a seguir en el análisis factorial:
1º. Mediante la opción “reducción de datos” del software estadístico SPSS se calcula la matriz de correlaciones para todas las variables.
A continuación, dentro del cuadro de diálogo del SPSS «extracción de factores» utilizamos el «método de componentes principales», matriz de correlaciones para el análisis, autovalores mayores que 1 como criterio para definir el número de componentes a seleccionar y la presentación de la solución factorial sin rotar. Con el método de componentes principales se pretende conseguir una combinación lineal de las variables, de modo que el primer componente principal sea el que explique la mayor proporción de la varianza de los datos; el siguiente componente será el que le siga en la explicación de la varianza, y así sucesivamente.
Expresado de otra manera, este procedimiento busca el factor que explique la mayor cantidad de la varianza en la matriz de correlación. Este recibe el nombre de “factor principal”. Esta varianza explicada se resta de la matriz original produciéndose una matriz residual. Luego se extrae un segundo factor de esta matriz residual y así sucesivamente hasta que quede muy poca varianza que pueda explicarse. Los factores así extraídos no se correlacionan entre ellos, por esta razón se dice que estos factores son ortogonales.
En la salida del SPSS se refleja información sobre los m componentes ordenados descendentemente. Para cada factor se muestra el autovalor (valor propio asociado) que es su varianza, el porcentaje de varianza total que es capaz de abarcar y el porcentaje acumulado de varianza explicada. Los “eigenvalue” (valores propios) pueden interpretarse como la cantidad de varianza explicada por cada factor. La “comunalidad”, es la cantidad de varianza que una variable comparte con las demás variables consideradas.
La solución factorial sin rotar es denominada matriz de componentes o matriz de cargas de los componentes. Las cargas son correlaciones entre las variables originales y los componentes, por eso altos valores de esos coeficientes (en valor absoluto) informan de los indicadores más fuertemente correlacionados con cada componente. Esto es, la “carga factorial” es la correlación entre las variables y los factores.
Se obtiene un gráfico (Gráfico de Sedimentación) que representa en el eje de las “x” el número de orden de los factores y en el eje de las “y”, los valores propios (eigenvalues). Muestra la forma en que van disminuyendo los valores propios, graficando el hecho de que el primer factor es el que más varianza explica.
2º. El siguiente paso consiste en realizar la rotación de componentes. De los diferentes métodos de rotación de componentes se aplica el Varimax. Este método es el más comúnmente usado, facilita la interpretación de los componentes.
La matriz de componentes sin rotar puede ser difícil de interpretar porque la mayoría de los componentes están relacionados con muchas variables. La matriz de componentes rotada es una nueva matriz que tiene una interpretación más clara. Conociendo qué significan las variables que están altamente correlacionadas con cada uno de los componentes se puede ofrecer una interpretación de estos asociada a la variable adecuación del centro de impactos.
El objetivo de la rotación de componentes es conseguir que cada variable no esté saturada en más de un factor, que cada factor deba tener pocas saturaciones altas y las restantes próxima a cero y que dos componentes distintos presenten saturaciones altas y bajas en diferentes variables.
En sí, el fin prioritario de la rotación es la de dar mayor interpretación científica a los componentes, la cual vendrá resaltada por el peso que aporte la variable al factor. De esta forma tendrán mayor importancia las variables que aporten mayor peso.
La denominación que debe adjudicarse a los componentes (factores) encontrados es algo subjetivo y requiere de una combinación de intuición y conocimiento de las variables.
El éxito de una rotación puede ser valorado con ayuda de gráficos que constituyen salidas del SPSS.
Para la interpretación de estos “Gráficos de Factores” (Gráfico de Saturaciones) se señalan las siguientes indicaciones generales:
Proximidades entre las variables: Dos o más variables muy correlacionadas positivamente se sitúan muy próximas. Dos o más variables muy correlacionadas negativamente están muy alejadas. Si son independientes, su distancia es del tipo medio.
Cuanto más alejada esté una variable del origen en un plano factorial mayor es la calidad de representación sobre ese plano.
Siempre se debe examinar la validez del análisis factorial
-
Un criterio de efectividad del análisis factorial es lograr explicar un alto porcentaje de la variabilidad total con un número bastante reducido de componentes principales. En total se eligen aquellos componentes que explican el 60 % de la varianza asumiendo el criterio de admitir como solución válida aquella que informa como mínimo del 60%.
-
La selección es buena si somos capaces de hacer una interpretación plausible de los componentes, aunque sea después de un proceso de rotación.
-
El análisis factorial tiene sentido cuando las variables estén suficientemente correlacionadas. Para examinar este criterio se utilizan diferentes métodos:
-
Test de Esfericidad de Bartlett: Comprueba que la matriz de correlaciones se ajusta a la matriz identidad (I), es decir ausencia de correlación significativa entre las variables. Esto muestra que la nube de puntos se ajusta a una esfera perfecta, expresando así la hipótesis nula por:
-
H0: R = I
es decir, que el determinante de la matriz de correlaciones es 1.
H0: |R| = 1
Se puede dar como válidos aquellos resultados que presenten un valor elevado del test y cuya significación sea menor a 0.05. En este caso se rechaza la hipótesis nula y se continúa con el análisis.
El determinante de la matriz de correlaciones: un determinante muy bajo indicará altas intercorrelaciones entre las variables, pero no debe ser cero (matriz no singular), pues esto indicaría que algunas de las variables son linealmente dependientes y no se podrían realizar ciertos cálculos necesarios en el análisis factorial. Un valor muy cercano a cero es una alerta de que la matriz de correlaciones está mal condicionada.
La medida de suficiencia de la muestra denominada Medida de Kaiser-Meyer-Olkin (KMO). Pequeños valores de KMO indican que el análisis de factor realizado con esas m variables no es adecuado, un valor de KMO = 0 informa que el análisis factorial es inadecuado mientras que un valor de KMO = 1 informa que todas las variables son adecuadas y el análisis de factor tiene máxima validez. Los valores entre 0.5 y 1 indican que es apropiado aplicar el análisis factorial.
Un ejemplo práctico
Para la definición de la adecuación del centro de impactos como factor que favorece el rendimiento en competición en la Pistola 50 metros (Hombres) se requiere el uso del análisis factorial.
Atendiendo a la naturaleza de las dimensiones del factor que favorece el rendimiento en competición, seis indicadores de las dimensiones “desplazamiento del punto de impacto disparo a disparo y desplazamiento del centro de impactos disparo a disparo” son sometidos en su conjunto a un análisis factorial con el propósito de reducir su número sin perder información sustancial y determinar cuáles de los indicadores obtenidos permiten valorar mejor la variable que se quiere medir, así como realizar agrupaciones de indicadores en otros nuevos a partir de los datos aportados por la muestra de 25 tiradores juveniles de Pistola 50 metros (Hombres).
Al extraer los factores con el método de componentes principales se consigue que los tres primeros componentes principales expliquen un 76.32 % de la varianza de los datos, de modo que se obtienen tres componentes que están representadas en la variable “adecuación del centro de impactos”.
La rotación de los componentes mediante el método Varimax nos permite ofrecer una interpretación científica de esos componentes de la variable en estudio.
A continuación se muestra la varianza de cada uno de los componentes (lo que se denomina “valor propio”), los porcentajes de varianza que es capaz de abarcar cada componente y el porcentaje acumulado de la varianza explicada.
De acuerdo con el criterio asumido de “parada” en el proceso de selección de p componentes principales con p < m se seleccionan tres componentes. El primero asociado al valor propio 2.085 es capaz de explicar por si solo un 34.75% de la varianza total de la muestra, el segundo asociado al valor propio 1.361 explica el 22.89% y junto con el componente 1, acumula el 57.44%. Los tres primeros componentes llegan a explicar el 76.32 % de la varianza total de la muestra lo que se considera satisfactorio. Los restantes componentes explican apenas el 23.68% de la varianza total de la muestra y ninguno de ellos por separado aportaría más que cualquiera de las variables. En el mismo Anexo 16 se muestra un gráfico que ilustra lo anterior. Se plotean los valores propios para los p componentes y muestran un rompimiento entre la pendiente de los mayores valores y el gradual recorrido de los restantes valores propios.
Tabla 1. Porcentaje de varianza explicada por cada uno de los componentes extraídos
|
Componentes |
Valor propio |
% de varianza |
% de varianza acumulada |
|
1 |
2.085 |
34.751 |
34.751 |
|
2 |
1.361 |
22.689 |
57.440 |
|
3 |
1.133 |
18.879 |
76.319 |
|
4 |
.635 |
10.590 |
86.909 |
|
5 |
.541 |
9.015 |
95.923 |
|
6 |
.245 |
4.077 |
100.000 |
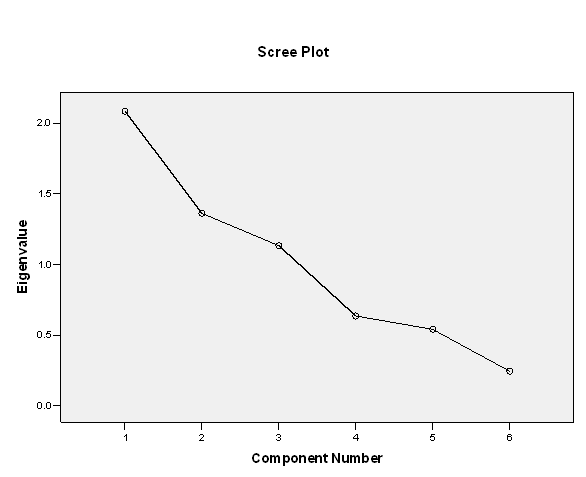
Gráfico 1. Ploteo de los valores propios para los p=6 componentes
En las tablas siguientes se puede apreciar la matriz de componentes (matriz de carga de los componentes) sin rotar y rotada. La matriz de carga es además la matriz de correlaciones entre las variables originales y los componentes. Para facilitar la apreciación de estas relaciones y ayudar a la interpretación de los componentes se han ordenado los coeficientes por la magnitud absoluta y se han omitido aquellos no mayor en valor absoluto que 0.5. Como se puede apreciar se consigue que cada variable no esté saturada en más de un componente.
Tabla 2. Matriz de componentes (matriz de carga de los componentes)
|
|
Componentes |
||
|
1 |
2 |
3 |
|
|
Radio del punto de impacto |
0.890 |
|
|
|
Distancia entre el centro de impactos precedente y el actual |
0.743 |
|
|
|
Distancia entre el punto de impactos precedente y el actual |
0.626 |
|
0.624 |
|
Ángulo generado por el punto de impacto |
|
0.815 |
|
|
Ángulo generado por el centro de impactos |
|
0.803 |
|
|
Radio del centro de impactos |
|
|
-0.746 |
Tabla 3. Matriz de componentes rotados (resultados del método varimax)
|
|
Componentes |
||
|
1 |
2 |
3 |
|
|
Distancia entre el punto de impactos precedente y el actual |
0.882 |
|
|
|
Distancia entre el centro de impactos precedente y el actual |
0.778 |
|
|
|
Radio del centro de impactos |
|
0.955 |
|
|
Radio del punto de impacto |
|
0.746 |
|
|
Ángulo generado por el centro de impactos |
|
|
0.828 |
|
Ángulo generado por el punto de impacto |
|
|
0.823 |
Los componentes se interpretan de la siguiente manera:
El primer componente se correlaciona positivamente con la distancia entre el punto de impacto precedente y el actual, así como la distancia entre el centro de impacto precedente y el actual. Por ello el componente 1 es interpretado como una medida del área de dispersión que se genera por el desplazamiento tanto del punto de impacto disparo a disparo como del centro de impactos.
El segundo componente se correlaciona positivamente con el radio del centro de impactos y del punto de impacto. Por ello el componente 2 es interpretado como una medida de la cercanía al cero en el desplazamiento tanto del punto de impacto disparo a disparo como del centro de impactos.
El tercer componente se correlaciona positivamente con el ángulo generado por el punto de impacto y el generado por el centro de impactos. Por ello el componente 3 es interpretado como una medida de la ubicación por cuadrante tanto del punto de impacto disparo a disparo como del centro de impactos en sus desplazamientos.
La conclusión fundamental de este análisis es que no es posible reducir el número de indicadores. Cada uno de esos componentes y las variables que lo representan (indicadores) aporta un peso considerable al factor “adecuación del centro de impactos”.
Los criterios de validez de un análisis factorial se cumplen en este caso.
-
Se logran seleccionar tres componentes de las seis variables que son capaces de explicar más del 60% de la variabilidad total de la muestra.
-
Se logra hacer una interpretación plausible de los componentes, después de un proceso de rotación.
-
Se cumple la condición imprescindible para la realización de un análisis estadístico multivariado corroborado por los resultados del test de esfericidad de Bartlett que verifica de forma multivariada la significación de los coeficientes de correlación entre los componentes (significación calculada 0.0000).
-
La matriz de correlaciones no está mal condicionada dado que su determinante no está muy cerca de cero (no está peligrosamente cerca de cero). (0<0.270<1)
-
La suficiencia de manera integrada de las variables consideradas no está tan cercana a cero (KMO = 0.512). Cuando esto ocurre el modelo del análisis factorial es adecuado.
Otras situaciones que ejemplifican la utilidad del análisis factorial en el deporte
Obtención de un criterio único que mida “rendimiento deportivo”
En un estudio del rendimiento de los esgrimistas cubanos a partir de diferentes criterios entre los que se encuentran: el lugar obtenido en la competencia, la efectividad -dada por la razón del número de victorias en N combates- y los toques efectuados, se desea obtener un criterio único que mida “rendimiento deportivo”. Aplicando el Análisis Factorial se obtiene lo deseado. (Morales, 1996)
Determinación de factores fundamentales en la preparación del deportista
En un estudio para determinar algunos factores fundamentales de la preparación física y técnica especial, los cuales “descubren” la influencia específica que ejerce el juego de baloncesto sobre el estado morfofuncional de las baloncestistas del alto rendimiento se emplea el análisis factorial. (Cintra, 1992)
Búsqueda de variables que expresen resumidamente relaciones subyacentes en la caracterización psicológica del escolar
Se realiza una investigación psicológica con niños de edad escolar, se miden características generales como son la edad, el sexo, la atención referida, la atención experimental, la intranquilidad, la impulsividad, la terquedad, el desarrollo escolar, hasta 40 variables, entre las cuales hay fuertes relaciones de correlación.
El análisis factorial debe ser capaz de reducir las variables originales X1, X2,..., X40 a un grupo reducido de factores, tal vez 10 o 12 factores: F1, F2,..., F10 independientes entre si y capaces de explicar la mayor parte de la variabilidad de la muestra. Se llama la atención de que los factores no son variables originales seleccionadas mediante cierto criterio, sino combinaciones lineales de todas ellas, determinadas por sus relaciones de correlación. En este sentido, son variables no directamente observables y que expresan resumidamente relaciones subyacentes en la caracterización psicológica del niño.
Conclusiones
La respuestas a las interrogantes ¿Qué es el análisis factorial? ¿Cuándo se utiliza? ¿Cómo se aplica?, el ejemplo práctico utilizando el SPSS que se presenta y otras situaciones que ejemplifican la utilidad del análisis factorial en el deporte sirven de guía para la aplicación de esta técnica estadística multivariada por los investigadores.
Bibliografía básica
-
Campistrous, L. y C. Rizo (2006). Indicadores e investigación educativa. En: Metodología de la investigación educacional. Desafíos y polémicas actuales. Colectivo de autores (eds.), Ciudad de La Habana, Editorial Ciencias Médicas.
-
Campoy, T.J. (2005). El cuestionario. Métodos de investigación social. Programa de Doctorado. Jaen, Universidad de Jaen.
-
Cintra Kindelán, Orestes: (1992). Factores de la efectividad de juego en el baloncesto. Ciudad de la Habana: Editorial Pueblo y Educación.
-
González, L. G. (2005). Determinantes psicológicos del rendimiento deportivo. Ciudad de la Habana, Psicología del deporte, Instituto de Medicina Deportiva.
-
Hernández, R., C. Fernández y P. Baptista (2003). Metodología de la Investigación México D.F., Mc Graw-Hill.
-
Mesa, M. (2001). Asesoría estadística con enfoque procesal en en la investigación científica aplicada al deporte. Tesis de grado (Doctor en Ciencias de la Cultura Física), Cuba, Instituto Superior de Cultura Física “Manuel Fajardo”.
-
Mesa, M. (2006). Asesoría estadística en la investigación aplicada al deporte. Ciudad de la Habana, Editorial José Martí.
-
Morales Águila, Antonio: (1996). Pruebas psicológicas específicas para el control del desarrollo de los procesos cognoscitivos en esgrimistas. Tesis de grado (Doctor en Ciencias Pedagógicas), Cuba, Instituto Superior de Cultura Física “Manuel Fajardo”.
-
Sabino, C.A. (1996). El proceso de investigaciones. Indicadores e índices. Buenos Aires, Editorial Lumen - Humanitas.
-
Vidaurreta, R. (2009). Adecuación del centro de impactos como factor que favorece el rendimiento en competición en tiradores de Pistola 50 metros (Hombres). Tesis de grado (Doctor en Ciencias de la Cultura Física), Cuba, Instituto Superior de Cultura Física “Manuel Fajardo”.
 |
|
|---|---|
|
revista
digital · Año 14 · N° 134 | Buenos Aires,
Julio de 2009 |
|