Revisión de los principales parámetros cinemáticos del lanzamiento en baloncesto
	*Estudiante de cuarto curso de Ciencias de la Actividad Física y el Deporte Alumno Interno del Laboratorio de Fisiología de la Universidad Europea Miguel de Cervantes, Valladolid. **Licenciada en Ciencias de la Actividad Física y el Deporte ***Dr. en Ciencias de la Actividad Física y el Deporte por la Universidad de León. Profesor Titular.  Responsable del Laboratorio de Fisiología Universidad Europea Miguel de Cervantes, Valladolid	Juan Martín Hernández* Beatriz Fernández Díez** Juan Azael Herrero Alonso*** martinhj@wanadoo.es (España)
	Resumen           Numerosos autores han estudiado los parámetros cinemáticos que influyen en la consecución de un lanzamiento en baloncesto. Por desgracia han sido realizados en condiciones experimentales muy dispares, lo que dificulta su comparación. Existen tres parámetros de lanzamiento que han sido tratados en todos ellos, y que son: ángulo, velocidad y altura de liberación. El propósito de este estudio es realizar una revisión que permita aglutinar los resultados obtenidos en unos y otros estudios y establecer patrones y causas de evolución del gesto técnico del lanzamiento. El ángulo de lanzamiento se ve delimitado por un rango que tiene por máximo 90º y mínimo f. Se encuentran múltiples diferencias en función de las condiciones experimentales en este parámetro. La velocidad de salida sigue un patrón de evolución similar en los diferentes trabajos, mientras que la altura de lanzamiento únicamente se ve modificada ante la presencia de un oponente, existiendo una tendencia clara a su aumento frente a la disminución de la distancia. Las interacciones entre todos los parámetros son consecuencia de las situaciones de juego y las adaptaciones del jugador, produciendo las modificaciones de uno de ellos grandes cambios en los otros. La presencia de un oponente se ha definido asimismo como otro de los grandes agentes de modificación de la técnica de lanzamiento.           Palabras clave: Lanzamiento. Baloncesto. Angulo de liberación. Velocidad de liberación. Altura de liberación.
	http://www.efdeportes.com/ Revista Digital - Buenos Aires - Año 13 - Nº 123 - Agosto de 2008

1 / 1

1.     Introducción

    El tiro es uno de los gestos más importantes del baloncesto. Constituye un elemento técnico de indispensable dominio para cualquier deportista que practique este deporte, ya que como es sabido, es el único modo de anotar puntos. El lanzamiento no es más que la propulsión de un móvil hacia un objetivo previamente definido. Cualquier desplazamiento de un móvil es propiciado por una fuerza capaz de variar su estado de reposo o de movimiento, según enuncia la primera ley de Newton. Así, la fuerza resultante por la cual el balón abandona la mano del jugador para proyectarse hacia el aro es consecuencia de la cadena cinemática que la precede (Hamilton y Reinschmidt, 1997). El objetivo de esta cadena cinemática es propulsar el balón con una combinación perfecta de velocidad y precisión, de modo que éste alcance el objetivo deseado.

    Para simplificar el análisis del lanzamiento en baloncesto, y tomando como referencia el método utilizado por Hamilton y Reinschmidt (1997), se considerará el balón como una esfera hueca que intersecciona con un plano paralelo al suelo en el que se encuentra contenido el aro. En adelante se denominará al vector resultante como Fr, y su módulo será igual a la velocidad del lanzamiento ó V. Para finalizar el ajuste de todos los parámetros de lanzamiento deberíamos considerar todas las variables representadas en la Figura 1 (Tan y Miller, 1982; Hamilton y Reinshmidt, 1997), aunque no todas dependen del lanzador. De este modo, se analizarán a lo largo del estudio las siguientes variables:

• Ángulo de lanzamiento (a en adelante): ángulo que forma el vector V_lanz con el plano del suelo en el momento en el que el balón pierde contacto con el lanzador. (Figura 1)

• Velocidad de lanzamiento (V en adelante): velocidad del balón medida en m*s^-1 en el momento en el que pierde el contacto con el lanzador. (Figura 1)

• Altura de lanzamiento (h en adelante): altura medida en m a la que el balón pierde el contacto con el lanzador. (Figura 1)

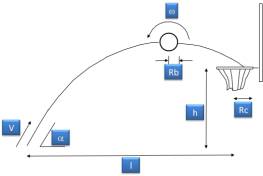
Figura 1. Variables que intervienen en un lanzamiento en baloncesto. Extraído de Hamilton y Reinshmidt, 1997.

    Se fijará para el análisis de las distancias el modelo de Miller y Barlett, 1996 (Figura 2), dividiéndolas en: cortas (2’74m), medias (4’57m) y largas (6’40m). Supondremos el balón como una esfera que se desplaza sin velocidad angular en el vacío.

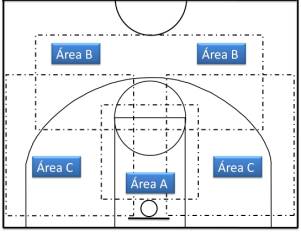
Figura 2. División del campo en zonas. A: zona de mayor densidad de lanzamiento de pívots; B: zona de mayor densidad de lanzamiento de los bases; C: zona de mayor densidad de lanzamiento de los bases. Adaptado de Miller y Barlett, 1996.

    Se ha analizado desde un punto de vista físico cuáles son los parámetros idóneos que conllevan la consecución de un lanzamiento eficiente, aunque en el gesto deportivo deben tenerse en cuenta las condiciones de realización de la tarea, el biotipo del lanzador (Ackland y cols., 1997), la situación de juego (Miller y Barlett, 1993), la presencia de uno o varios oponentes (Rojas, 2000), la fatiga central y periférica, la distancia de lanzamiento (Elliott, 1992; Hamilton y Reinschmidt, 1997; Miller y Barlett, 1996) etc. Por todos estos motivos debe evaluarse, con respecto a los patrones ideales, la capacidad de adaptación de nuestro deportista. Tras revisar la literatura, se ponen de manifiesto diferencias entre los resultados obtenidos en aquellos estudios con un cariz teórico o descriptivo, realizados por medio de simulaciones (Hamilton y Reinschmidt, 1997) o en condiciones de laboratorio (Elliott, 1989; Miller y Barlett, 1996) y los realizados ante la presencia de obstáculos, oponentes o en situaciones reales de juego (Bishop y Hay, 1972; Elliott, 1992; Miller y Barlett, 1993; Rojas, 2000); es decir, en aquellas situaciones en las que interviene la incertidumbre característica del baloncesto y que conllevan, por tanto, una adaptación del lanzamiento.

    No se ha encontrado en la última década ningún artículo que aglutine las conclusiones sobre cinemática del lanzamiento de varios trabajos. El objetivo de esta revisión es, por tanto, describir cuáles son las variaciones que tienen lugar en los principales parámetros de lanzamiento y el porqué de dichas variaciones, así como desentrañar las posibles causas de las modificaciones adoptadas por los jugadores entre las situaciones experimentalmente controladas y las situaciones reales de juego.

2.     Variables determinantes en el lanzamiento

2.1.     Ángulo de lanzamiento

    El ángulo con el que el balón abandona la mano del lanzador no puede tomar cualquier valor desde una distancia dada; es decir, existe un rango fuera del cual es imposible encestar aún modificando el resto de los parámetros. Este rango viene delimitado por un ángulo máximo, siempre constante e igual a 90º y un ángulo mínimo o f, delimitado por la línea que une el balón con el punto del aro más cercano al jugador y una línea paralela al suelo que pase por el balón, como puede verse en la Figura 3.

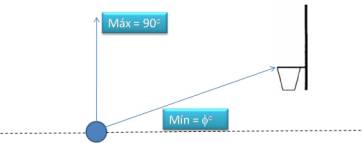
Figura 3. Ángulos máximo y mínimo de lanzamiento para una distancia y altura dadas.

    El ángulo de lanzamiento medio oscila entre los 50 y los 51º (Elliott, 1992; Miller y Barlett, 1993 y 1996; Hamilton y Reinschmidt, 1997; Rojas 2000). Llaman poderosamente la atención las diferencias encontradas entre los datos de los estudios de simulación, los estudios en laboratorio y aquellos realizados en situaciones reales de juego. En la Figura 4 están reflejados los datos referentes a este parámetro obtenidos en varios estudios. Manteniendo constante el parámetro de altura de lanzamiento (Miller y Barlett, 1993), es lógico pensar que cuanto más cerca esté el jugador de la canasta, mayor deberá ser el ángulo de lanzamiento del balón, aunque esta figura refleja patrones bien distintos. La rigidez de los patrones de lanzamiento elaborados por simulación o los obtenidos en condiciones de laboratorio hace que los investigadores no sean capaces de elaborar un modelo que tenga en cuenta las adaptaciones del deportista. Al aumentar la incertidumbre del medio en el que se realiza el lanzamiento y convertirlo en una tarea motriz abierta, muchas potenciales variables contaminadoras de la investigación en laboratorio intervienen en él. Así, el ángulo de lanzamiento puede verse modificado por el jugador de forma consciente ante agentes como la presencia de un oponente, la distribución y presión defensivas, la situación de los compañeros, o la propia posición del jugador. De forma inconsciente, las causas de modificación pueden ser debidas a la fatiga de los grupos musculares responsables del lanzamiento o la presión psicológica. Todo ello revierte en que en situaciones reales de juego y ante la presencia de un oponente se produce una variación de la técnica por la cual el valor del ángulo de salida tiende a verse incrementado de manera significativa (p<0,05) en un 4,9%. (Rojas, 2000). Este dato, así como los asombrosos resultados obtenidos por Elliott (1992) y Miller y Barlett (1993), únicamente muestra la media desde todas las distancias y posiciones de juego. Podría ser, por tanto, justificado por la menor presión ejercida por la defensa en las distancias largas, haciendo que en las distancias cortas los valores se incrementen respecto al ideal como señala Rojas (2000).

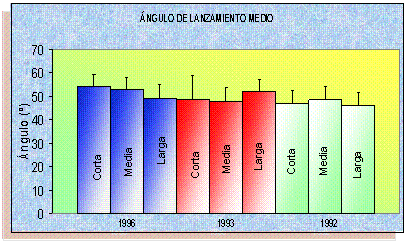
Figura 4. Ángulos de lanzamiento medios desde cada una de las tres posiciones de juego descritas. Adaptado de Miller y Barlett (1996). Estudio realizado en situación controlada de laboratorio y sin la presencia de un oponente. Estudio realizado por medio de recogida de datos en situación real de juego. Adaptado de Miller y Barlett (1993) Estudio realizado en situación controlada de laboratorio con la presencia de un oponente. Adaptado de Elliott (1992).

2.2.     Velocidad de lanzamiento

    Este parámetro se define como el módulo del vector responsable de propulsar el balón desde la mano del lanzador hasta el aro, y es función directa de la distancia de lanzamiento y el ángulo de salida, aunque con patrones de evolución diferentes. Se ha definido el ángulo de 45º como óptimo para la proyección de móviles desde un punto de vista físico (Hay, 1993), y manteniendo este valor en un rango de distancias que permitan localizarlo dentro del rango de lanzamiento (ver ángulo de lanzamiento), se observa cómo el valor de V se incrementa de forma lineal (Hamilton y Reinschmidt, 1997). Así lo corroboran Miller y Barlett (1996), en cuyo trabajo los aleros mantuvieron su rango de lanzamiento desde todas las distancias entre los 50±7º y los 52±6º. Una variación tan pequeña se tradujo en una evolución de la velocidad lineal, con un DV de 1,01m*s^-1 entre las distancias cortas y medias y de 1,08m*s^-1 entre distancias medias y largas. En cambio, si mantenemos fija una distancia de lanzamiento y se establece un a óptimo para esa distancia, todos los valores que tome a por encima del ideal, aumentarán de forma exponencial el módulo de V, tendiendo a infinito a medida que nos acerquemos al ángulo máximo (90º). Esto se supone obviando la resistencia del aire y el efecto que pudiera tener la velocidad angular del balón en su trayectoria.

    Los estudios consultados, recogen en todos los casos que V se incrementa de forma directamente proporcional a la distancia de lanzamiento, como puede observarse en la Figura 5, independientemente de las circunstancias en las que se lleve a cabo la medición y de las del lanzador.

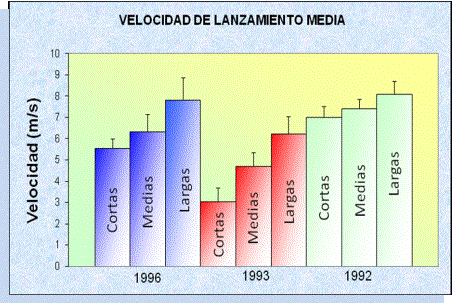
Figura 5. Velocidades de lanzamiento medias desde cada una de las tres posiciones de juego descritas. Adaptado de Miller y Barlett (1996). Estudio realizado en situación controlada de laboratorio y sin la presencia de un oponente. Estudio realizado por medio de recogida de datos en situación real de juego. Adaptado de Miller y Barlett (1993). Estudio realizado en situación controlada de laboratorio con la presencia de un oponente. Adaptado de Elliott (1992).

    Si se observa la figura, puede apreciarse que existen diferencias en los valores de V entre los estudios de Miller y Barlett (1993 y 1996), así como entre el estudio de estos autores (1993) y el de Elliott (1992). La reducción de V en situación real de juego puede deberse a un aumento de la presión defensiva, que tiene como resultado un aumento de la altura de lanzamiento (Bishop y Hay, 1979; Rojas, 2000) y la mencionada disminución de V, aunque no se ha encontrado ningún estudio en la literatura que demuestre una relación estadística fuerte y prediga la magnitud y el sentido de las relaciones establecidas entre los tres parámetros. Esta hipótesis que relaciona el incremento de la altura de liberación con el descenso de la velocidad de lanzamiento se relaciona asimismo con las diferencias reflejadas en la Tabla 1 en el estudio de Miller y Barlett (1996) entre los bases y el resto de los jugadores. Desde distancias largas, la velocidad de lanzamiento de los jugadores de esta demarcación es significativamente superior (p<0,01) a la del resto, uniéndose a la reflexión anterior en que éstos jugadores son los de menor estatura media y, por tanto, en los que el valor de h es menor.

Velocidad de lanzamiento	Distancia de lanzamiento (m)
	2,74	4,57	6,40
Bases	5,58 ± 0,48	6,27 ± 1,25	8,39 ± 0,49*
Aleros	5,27 ± 0,52	6,28 ± 0,57	7,36 ± 1,28
Pívots	5,71 ± 0,29	6,41 ± 0,67	7,68 ± 1,40

Tabla 1. Velocidad de lanzamiento en cada una de las tres posiciones. Adaptado de Miller y Barlett (1996)

*Diferencias significativas (p<0,01) comparado con los bases (2,74m), con aleros (desde todas las posiciones) y pívots (2,74m).

2.3.     Altura de lanzamiento

    Se asume la altura de lanzamiento como la distancia medida en metros que hay desde el balón en el momento que abandona la mano del lanzador hasta su proyección en el suelo.

    No existen diferencias significativas en la altura de lanzamiento en función de la distancia, pero sí existe una tendencia clara a disminuir la altura a medida que el lanzamiento se hace desde distancias mayores (Elliott, 1992; Miller y Barlett, 1993). Evoluciona de este mismo modo el tiempo transcurrido desde el despegue hasta el momento de liberación del balón (Elliott, 1992; Miller y Barlett, 1993). Esto indica que los lanzamientos desde cortas distancias se hacen desde alturas mayores y el balón se libera a un alto porcentaje de la altura de dicho salto, mientras que en las distancias largas el tiempo de vuelo es muy corto, así como el tiempo que transcurre entre el despegue y el lanzamiento.

    En un lanzamiento, se producen multitud de fuerzas en los tres ejes del movimiento que son modificadas por los jugadores en función de las circunstancias en las que se realice el lanzamiento. Elliott (1989) descubrió, por medio de un análisis dinámico del lanzamiento apoyado por plataformas de fuerzas, que las mujeres tendían a dotar a su salto de una componente horizontal más acusada que los hombres. Esto les permitía llegar al momento de liberación más cerca de la canasta y con un vector resultante del salto más próximo al necesario para propulsar el balón hacia el aro. Por medio de esta peculiar técnica de lanzamiento se logra suplir la falta de fuerza en los grupos musculares que intervienen en la cadena cinemática responsable del lanzamiento. Este descubrimiento de Elliott (1989) puede aplicarse cuidadosamente al caso que se presenta en el patrón de evolución de la altura de lanzamiento. Si observamos la gráfica fuerza-tiempo de un salto, puede apreciarse cómo hay un punto que corresponde a la elevación de los talones del suelo en el que el sujeto no es capaz de imprimir aceleración al centro de masas (CM). A partir de ese punto el CM del sujeto comienza a perder velocidad debido al efecto de la gravedad. Si esto lo trasladamos a un lanzamiento, podría resultar más efectiva la ganancia en fuerza que en tiempo de vuelo, es decir, si el jugador lanzase el balón en el momento de máxima aceleración del salto, el móvil sería propulsado con una fuerza mucho mayor que si lo hace en el punto de máxima altura en el que la velocidad vertical es 0m*s^-1 y la aceleración es -9’8m*s^-2. Esto se pone de manifiesto la Tabla 2, en la que llama poderosamente la atención que los pívots desde distancias largas lanzan atendiendo a este criterio; liberan el balón antes del despegue. La realización de lanzamientos de este tipo podría explicar al tiempo la menor altura obtenida desde largas distancias, así como los menores tiempos de vuelo registrados.

Tiempo despegue-lanzamiento (media ± desviación estándar)	Distancia de lanzamiento (m)
	2,74	4,57	6,40
Bases	0,15 ± 0,16	0,10 ± 0,12	0,10 ± 0,12
Aleros	0,15 ± 0,15	0,10 ± 0,09	0,02 ± 0,04
Pívots	0,08 ± 0,26	0,02 ± 0,15	-0,02 ± 0,02

Tabla 2. Tiempo de despegue-lanzamiento en cada una de las tres posiciones de juego. Adaptado de Miller y Barlett (1996)

    La evolución del salto es distinta en situaciones reales de juego que en condiciones de laboratorio. Ante la presencia de un oponente se disminuyen de forma significativa los tiempos de vuelo y la altura máxima del CM (Rojas, 2000). La trayectoria del centro de gravedad desde el momento del despegue hasta el aterrizaje describe una parábola más o menos abierta en función de la distribución de fuerzas inicial. Ante la presencia de un oponente, la parábola que describe el CM tiende a abrirse, y su máximo desciende. Si a este hecho se le añade una extensión de los miembros del tren superior, y una flexión de los miembros del tren inferior, el CM se mueve en consonancia con el desplazamiento de los segmentos corporales, por lo que en este caso tiende a ascender, a retardar su caída. La elevación por encima de las cotas medias de los miembros del tren superior produce asimismo que el lanzamiento se efectúe desde una altura mayor, pudiendo rebasar así la presión defensiva.

3.     Conclusiones

• Existen tres parámetros fundamentales para el estudio del lanzamiento en baloncesto: ángulo, velocidad y altura de salida del balón.

• El ángulo de salida se incrementa ante la presencia de un oponente.

• La velocidad de lanzamiento es función directa del ángulo de salida y se incrementa de forma exponencial con respecto a este parámetro, alcanzando su máximo en los 90º.

• La altura de lanzamiento se reduce de manera directamente proporcional a la distancia.

• Ante la presencia de un oponente aparece el efecto hang in the air, por el cual la altura de liberación se incrementa a pesar de no hacerlo la altura del centro de masas y el tiempo de vuelo.

• Existen grandes diferencias en los resultados obtenidos en condiciones controladas y los obtenidos en situaciones reales de juego, o al menos, ante la presencia de un oponente.

• Son necesarios nuevos estudios en situación real de juego o en condiciones controladas, aunque siempre ante la presencia de un oponente, de modo que se obtengan datos más acordes con la realidad del juego y, por consiguiente, con una mayor aplicabilidad.

Bibliografía

• Ackland, T.R., Schreiner A.B., Kerr D.A. (1997) Absolute size and proportionality characteristics of World Championship female basketball players. Journal of Sports Sciences 15(5):485-90.

• Beard, B. (1991) El jugador completo de baloncesto. Preparación, técnica, entrenamiento y el juego. Hispano Europea, S.A., Barcelona.

• Bishop, D.R., Hay, J.G. (1972) Basketball: the mechanics of hanging in the air. Medicine and Science in Sports, 11 (3), 274-277.

• Button, C., MacLeod, M., Sanders, R., Coleman, S. (2003) Examining movement variability in the basketball free-throw action at different skill levels. Research quarterly for Exercice and Sport, 74(3), 257-269.

• Elliott, B. (1992) A kinematic comparison of the male and female two-point and three-point jump shots in basketball, The Australian Jornal of Science and Medicine in Sport, December.

• Hamilton G.R., Reinschmidt (1997) Optimal trajectory for the basketball free throw, Journal of Sports Sciences, 15, 491-504.

• Hay, J. (1993) Biomechanics of Sports Techniques, Prentice Hall, Upper Saddle River, NJ.

• Liu, S., Burton, A.W. (1999) Changes in basketball shooting patterns as function of distance. Perceptual and Motor Skills, 89, 831-845.

• Mack, G.M. (1993) Effects of time and movements of the preshot routine on free throw shooting. Perceptual and Motor Skills,2, 567-573.

• Mauel, L.T. (1999) Principios biomecánicos, Revista de entrenamiento deportivo, 13(2).

• Miller, S. y Barlett, R. (1993) The effects of increased shooting distance in the basketball jump shot, Journal of Sports Sciences, 11, 285-293.

• Miller, S. y Barlett, R. (1996) The relationship between basketball shooting kinematics, distance and playing position. Journal of Sports Sciences, 14, 243-253.

• Rojas, F.J., Cepero, M., Oña, A, Gutiérrez, M. (2000) Kinematic adjustments in the basketball jump shot against an opponent, Ergonomics, 43 (10), 1651-1660.

• Tan, A. Y Miller, G. (1982) Kinematics of the free throw in basketball. American Journal of Physiology. 49(6), 542-544.

Otros artículos sobre Baloncesto | Básquetbol

revista digital · Año 13 · N° 123 | Buenos Aires, Agosto de 2008   © 1997-2008 Derechos reservados