1 / 1

Introducción

    La modalidad deportiva acuática de la que se va a realizar este estudio es el waterpolo. Aunque a día de hoy es conocido y practicado en todo el mundo se trata de un deporte joven, ya que según Majoni (1954) apareció a partir de la segunda mitad del siglo XIX, en Gran Bretaña, producto de la Revolución Industrial. El waterpolo es un deporte acuático de equipo, sujeto a unas normas e institucionalizado, que se practica en una superficie limitada de piscina entre dos conjuntos de siete jugadores de campo (seis jugadores y portero) y con la finalidad de introducir el balón en la portería contraria (Lloret, 1994). Posteriormente (1995), el mismo autor propone definir el waterpolo como: deporte reglamentado de colaboración y oposición, que se comunica estratégicamente a través de la ejecución de unas acciones de juego en el medio acuático, portadoras de significación práxica, implícita o explícita, y cuya finalidad sería la interacción de marca entre los conjuntos integrantes del duelo simétrico.

    La meta intrínseca de la práctica deportiva encauzada hacia la competición es el éxito en la misma, es decir, la consecución de los mejores resultados posibles y la superación de los demás contendientes. El entrenamiento deportivo ha constituido en el ámbito del deporte el medio tradicional empleado para mejorar la preparación y así poder obtener unos mejores resultados en la competición. En un principio una ejercitación física perseverante vinculada a la disciplina deportiva en cuestión podía hacer competitivos a los deportistas. Pero esto pertenece al pasado. El éxito deportivo ha llegado a ser en la actualidad tremendamente difícil. La preparación que hoy día necesita un deportista o un equipo para ser competitivo a alto nivel, se ha ido haciendo tremendamente compleja y sofisticada. Es evidente pues, que la evolución del entrenamiento deportivo ha sido uno de los factores clave que más ha contribuido al mencionado incremento en el rendimiento deportivo. El entrenamiento no sólo se ha visto beneficiado del avance de las ciencias auxiliares o de apoyo (fisiología, biomecánica, psicología, etc.), sino que principalmente a lo largo de los últimos tiempos se ha ido impregnando de los planteamientos del método científico. De modo que la propia sistemática y organización del entrenamiento empiezan a constituir en si mismos una naciente y compleja aplicación científica.

    Si se quiere realizar una evaluación de la táctica de un equipo de waterpolo, en un entrenamiento o en competición, sería muy complejo intentar abordarla como un todo. De ahí que, resulta necesario dividir esa situación de juego en microsituaciones que mantengan la estructura de la modalidad deportiva. Así pues, se estaría frente a diversas unidades diferenciadas que facilitarían en gran medida su cuantificación, valoración y actuación; siendo éstas las fases de la evaluación táctica deportiva. El contexto en el que se desarrolla cada microsituación se denomina marco situacional, quedando definido éste como el conjunto de comportamientos motores presentes en la dinámica de juego en los deportes de equipo, determinada por los factores de: simetría de los equipos, organización de los sistemas tácticos de juego y posesión del móvil. En el caso concreto del waterpolo, se pueden distinguir cuatro: a) igualdad numérica, b) transicional, c) desigualdad numérica y d) penalti. En el caso que nos ocupa, el marco de la desigualdad numérica en waterpolo es una microsituación de juego determinada por el reglamento en la cual se altera el número de jugadores en alguno de los dos equipos. Podemos distinguir, en función de la infracción, una duración temporal, 20" ó recuperación - pérdida de la posesión del móvil, o definitiva sin sustitución, resto del partido. Asimismo, para el primer caso podemos diferenciar el número de jugadores, simple o doble, precisando a su vez la posesión o no del móvil. La desigualdad numérica temporal simple en waterpolo es una microsituación de juego determinada por el reglamento en la cual está alterado el número de jugadores, +/-1, en alguno de los dos equipos durante un máximo de 20" o hasta la recuperación de la posesión del móvil por parte del equipo infractor. La desigualdad numérica temporal doble en waterpolo es una microsituación de juego determinada por el reglamento en la cual está alterado el número de jugadores, +/- 2, en alguno de los dos equipos durante un máximo de 20", hasta la recuperación de la posesión del móvil por parte del equipo infractor o hasta la reincorporación de alguno de los dos jugadores excluidos temporalmente. La desigualdad numérica definitiva en waterpolo es una microsituación de juego determinada por el reglamento en la cual está alterado el número de jugadores en alguno de los dos equipos por el resto del partido (Argudo, 2005).

    Al finalizar un partido de waterpolo, ¿pueden conocerse los aspectos que han determinado la victoria o la derrota? Basándonos en los resultados obtenidos por la cuantificación de las acciones de juego, podemos valorar la eficacia de las mismas a partir de unos coeficientes (Argudo, 2002). La eficacia, según Gayoso (1983), podemos considerarla como el resultado de las acciones correctamente ejecutadas dentro de una cantidad de intentos o ensayos. Este mismo autor considera las mediciones y evaluaciones de los comportamientos tanto in vivo como in vitro, de capital importancia.

    En el caso concreto del waterpolo, se pueden mencionar trabajos de conceptualización, elaboración de instrumentos de evaluación y primeros estudios de los valores de eficacia (Argudo, 2000; Argudo & Lloret, 2006; Argudo & Ruiz, 2006a, b; Canossa, Garganta & Lloret, 2001; Dopsaj & Matkovic, 1999; Enomoto, 2004; Lloret, 1994, 1999; Platanou, 2001, 2004; Sarmento, 1991; Sarmento & Magalhaes, 1991) que exponen unas fórmulas para aclarar y justificar el nivel de trabajo ofensivo y defensivo en los partidos de esta modalidad deportiva acuática. Así pues, un coeficiente de eficacia es una fórmula matemática que determina un valor numérico resultante de la relación entre las acciones, táctica individual, o los procedimientos tácticos, táctica grupal, o los sistemas tácticos de juego, táctica colectiva, ejecutados y la cantidad de intentos realizados en las diferentes microsituaciones de juego. Como resultante de los mismos tendríamos un valor de eficacia, que se trata de un indicador de rendimiento, numérico, que nos revela la información necesaria para continuar o modificar la planificación o programación del contenido táctico en el entrenamiento o en la competición (Argudo, 2005).

    Los objetivos de este trabajo fueron: a) calcular en las microsituaciones de juego en la desigualdad numérica temporal simple con o sin posesión del balón los valores de eficacia y b) analizar la relación entre la condición de ganador o perdedor al finalizar el partido y los valores de eficacia. La hipótesis de este trabajo fue que los equipos ganadores obtienen valores de eficacia más altos que los perdedores.

Método

Población

    La muestra estudiada ha sido extraída del X Campeonato del Mundo de Barcelona 2003. La población objeto de estudio fueron los 32 equipos nacionales que participaron en el mismo, por lo que se les supone un nivel de homogeneidad. En el mencionado Campeonato se disputaron 96 partidos, de los cuales se seleccionaron para el presente trabajo los 46 partidos de waterpolo masculino y los 47 partidos de waterpolo femenino cuyo resultado final no fue un empate.

Instrumentos

    Todos los partidos seleccionados han sido analizados con el software Polo análisis v 1.0 directo (Argudo, Alonso y Fuentes, 2005), instrumento desarrollado para la evaluación táctica cuantitativa en waterpolo en tiempo real (ver Figuras 1 y 2).

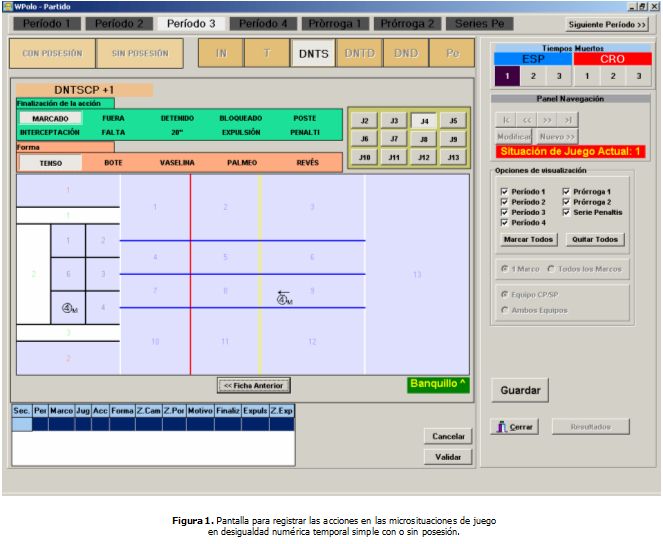
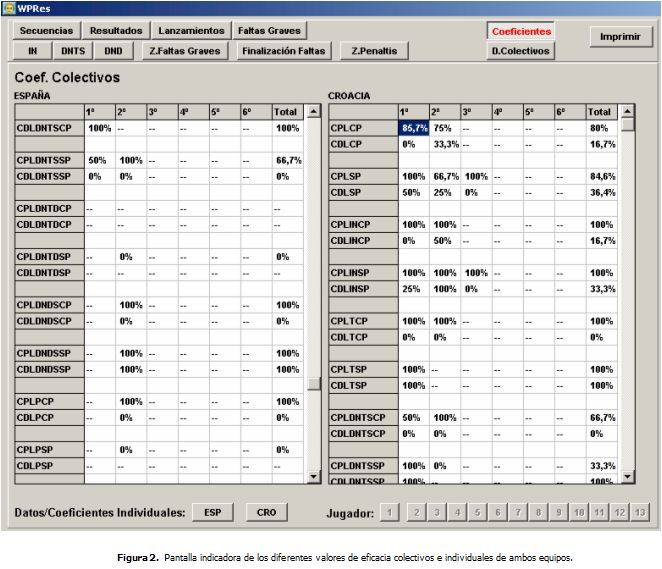
    Las variables objeto de estudio han sido la condición de ganador o perdedor al terminar el partido y los valores de eficacia obtenidos a partir de los coeficientes propuestos para evaluar esta microsituación de juego que se desarrollan a continuación:

    1. Coeficiente de posibilidad de lanzamientos en desigualdad numérica temporal simple con posesión. Fórmula matemática que determina un valor numérico de la relación entre los lanzamientos realizados y las microsituaciones de juego con posesión.
CPLDNTSCP = Σ lanzamientos realizados x 100 / Σ microsituaciones con posesión.

    2. Coeficiente de concreción de lanzamientos en desigualdad numérica temporal simple con posesión. Fórmula matemática que determina un valor numérico de la relación entre los lanzamientos marcados y las microsituaciones de juego con posesión.
CCLDNTSCP = Σ lanzamientos marcados x 100 / Σ microsituaciones con posesión.

    3. Coeficiente de definición de lanzamientos en desigualdad numérica temporal simple con posesión. Fórmula matemática que determina un valor numérico de la relación entre los lanzamientos marcados y los lanzamientos realizados.
CDLDNTSCP = Σ lanzamientos marcados x 100 / Σ lanzamientos realizados.

    4. Coeficiente de resolución de lanzamientos en desigualdad numérica temporal simple con posesión. Fórmula matemática que determina un valor numérico de la relación entre los lanzamientos marcados y los lanzamientos a portería.
CRLDNTSCP = Σ lanzamientos marcados x 100 / Σ lanzamientos realizados - (Σ lanzamientos fuera + Σ lanzamientos bloqueados + Σ lanzamientos postes).

    5. Coeficiente de precisión de lanzamientos en desigualdad numérica temporal simple con posesión. Fórmula matemática que determina un valor numérico de la relación entre los lanzamientos a portería y las microsituaciones de juego con posesión.
CPRLDNTSCP = [Σ lanzamientos realizados - (Σ lanzamientos fuera + Σ lanzamientos bloqueados + Σ lanzamientos postes)] x 100 / Σ microsituaciones con posesión.

    6. Coeficiente de exactitud de lanzamientos en desigualdad numérica temporal simple con posesión. Fórmula matemática que determina un valor numérico de la relación entre los lanzamientos a portería y los lanzamientos realizados.
CELDNTSCP = [Σ lanzamientos realizados - (Σ lanzamientos fuera + Σ lanzamientos bloqueados + Σ lanzamientos postes)] x 100 / Σ lanzamientos realizados.

    Todos estos coeficientes cuanto mayor sea el valor numérico indicarán mayor eficacia. Además se establecen entre ellos una serie de relaciones:

1. CDLDNTSCP se debe aproximar o igualar a CELDNTSCP.

2. CCLDNTSCP se debe aproximar o igualar a CPRLDNTSCP.

3. CCLDNTSCP se debe aproximar o igualar a CPLDNTSCP.

4. CPRLDNTSCP se debe aproximar o igualar a CPLDNTSCP.

    7. Coeficiente de posibilidad de lanzamientos en desigualdad numérica temporal simple sin posesión. Fórmula matemática que determina un valor numérico de la relación entre los lanzamientos recibidos y las microsituaciones de juego sin posesión.
CPLDNTSSP = Σ lanzamientos recibidos x 100 / Σ microsituaciones sin posesión.

    8. Coeficiente de concreción de lanzamientos en desigualdad numérica temporal simple sin posesión. Fórmula matemática que determina un valor numérico de la relación entre los lanzamientos encajados y las microsituaciones de juego sin posesión.
CCLDNTSSP = Σ lanzamientos encajados x 100 / Σ microsituaciones sin posesión.

    9. Coeficiente de definición de lanzamientos en desigualdad numérica temporal simple sin posesión. Fórmula matemática que determina un valor numérico de la relación entre los lanzamientos encajados y los lanzamientos recibidos.
CDLDNTSSP = Σ lanzamientos encajados x 100 / Σ lanzamientos recibidos.

    10. Coeficiente de resolución de lanzamientos en desigualdad numérica temporal simple sin posesión. Fórmula matemática que determina un valor numérico de la relación entre los lanzamientos encajados y los lanzamientos a portería.
CRLDNTSSP = Σ lanzamientos encajados x 100 / Σ lanzamientos recibidos - (Σ lanzamientos fuera + Σ lanzamientos bloqueados + Σ lanzamientos postes).

    11. Coeficiente de precisión de lanzamientos en desigualdad numérica temporal simple sin posesión. Fórmula matemática que determina un valor numérico de la relación entre los lanzamientos a portería y las microsituaciones de juego sin posesión.
CPRLDNTSSP = [Σ lanzamientos recibidos - (Σ lanzamientos fuera + Σ lanzamientos bloqueados + Σ lanzamientos postes)] x 100 / Σ microsituaciones sin posesión.

    12. Coeficiente de exactitud de lanzamientos en desigualdad numérica temporal simple sin posesión. Fórmula matemática que determina un valor numérico de la relación entre los lanzamientos a portería y los lanzamientos recibidos.
CELDNTSSP = [Σ lanzamientos recibidos - (Σ lanzamientos fuera + Σ lanzamientos bloqueados + Σ lanzamientos postes)] x 100 / Σ lanzamientos recibidos.

    Todos estos coeficientes cuanto menor sea el valor numérico indicarán mayor eficacia. Además se establecen entre ellos una serie de relaciones:

1. CDLDNTSSP se debe aproximar o igualar a CELDNTSSP.

2. CCLDNTSSP se debe aproximar o igualar a CPRLDNTSSP.

3. CCLDNTSSP se debe aproximar o igualar a CPLDNTSSP.

4. CPRLDNTSSP se debe aproximar o igualar a CPLDNTSSP.

    13. Coeficiente de lanzamientos bloqueados recibidos en desigualdad numérica temporal simple. Fórmula matemática que determina un valor numérico de la relación entre los lanzamientos bloqueados recibidos y los lanzamientos realizados.
CLBRDNTS = Σ lanzamientos bloqueados recibidos x 100 / Σ lanzamientos realizados.

    14. Coeficiente de lanzamientos bloqueados hechos en desigualdad numérica temporal simple. Fórmula matemática que determina un valor numérico de la relación entre los lanzamientos bloqueados hechos y los lanzamientos recibidos.
CLBHDNTS = Σ lanzamientos bloqueados hechos x 100 / Σ lanzamientos recibidos.

    Mientras en el primer coeficiente cuanto menor sea el valor numérico indicará mayor eficacia, en el segundo es al contrario. Además se establece entre ellos una relación:

1. CLBHDNTS debe superar a CLBRDNTS.

Procedimiento

    El método de filmación partía del enfoque inicial al centro del terreno de juego, para una vez que uno de los dos equipos entraba en posesión del balón realizar una técnica de barrido centrando la imagen en el medio campo donde se desarrollaba la acción de juego. La observación de los partidos se hizo de forma consensuada entre dos especialistas entrenados (Anguera et al., 2000; Anguera, 2003).

Análisis estadístico

    Las pruebas de homogeneidad de varianza se calcularon a través del estadístico de Levene. Posteriormente se realizó una ANOVA de un solo factor seguida por la prueba de Tukey para el análisis de las diferencias estadísticamente significativas entre los valores de eficacia en el igualdad numérica y la condición de ganador o perdedor al finalizar el partido. Todo el tratamiento estadístico mencionado se realizó con el paquete estadístico SPSS 12.0, aceptándose un nivel de confianza del 95% y una probabilidad de error del 5% (nivel de significación de .05).

Resultados

    El análisis estadístico de la comparación entre los valores de eficacia obtenidos en las microsituaciones de juego en desigualdad numérica temporal simple con y sin posesión, ha proporcionado los siguientes resultados, tal y como se presentan en la Tabla 1 y 2.

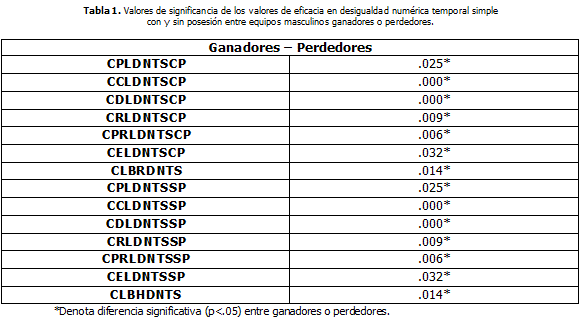
    De la interpretación de los datos se obtuvo que en todos los valores de eficacia los equipos masculinos ganadores presentan diferencias significativas frente a los perdedores.

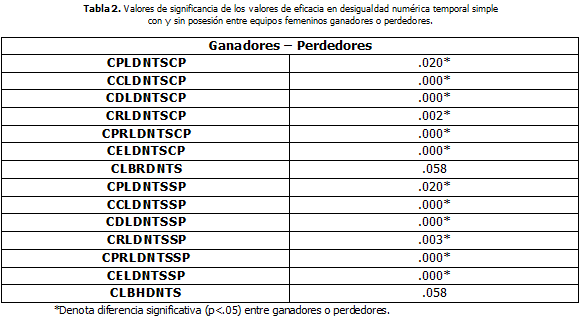
    Del análisis de los resultados se extrajo que los equipos femeninos ganadores en el CLBRDNTS y en el CLBHDNTS frente a los equipos perdedores, no presentan diferencias significativas p<.058 en ambos casos. Por el contrario los valores de eficacia obtenidos por los equipos ganadores en el CCLDNTSCP, en el CDLDNTSCP, en el CPRLDNTSCP, en el CELDNTSCP, CCLDNTSSP, en el CDLDNTSSP, en el CPRLDNTSSP y en el CELDNTSSP frente a los equipos perdedores, si presentan diferencias significativas p<.000. También, los valores de eficacia obtenidos por los equipos ganadores en el CPLDNTSCP y en el CPLDNTSSP p<.020, en el CRLDNTSCP p<.002 y en el CRLDNTSSP p<.003 frente a los equipos perdedores, presentan diferencias significativas.

Discusión y conclusiones

    Comparando los datos obtenidos en este estudio con trabajos anteriores de Argudo (2000), apreciamos que entre los equipos masculinos con la condición de ganador no encontramos coincidencias en el CCLDNTSCP p<.433, en el CDLDNTSCP p<.765, en el CCLDNTSSP p<.433 y en el CDLDNTSSP p<.765. Igualmente entre los equipos femeninos con la condición de ganador no encontramos coincidencias en el CCLDNTSCP p<.444, en el CDLDNTSCP p<.993, en el CCLDNTSSP p<.444 y en el CDLDNTSSP p<.993.

    Como conclusión principal de la evaluación táctica cuantitativa de las microsituaciones de juego en desigualdad numérica temporal simple con y sin posesión del balón en waterpolo del X Campeonato del Mundo de 2003, realizada en los partidos masculinos podemos inferir que, en todos los coeficientes de eficacia existen diferencias significativas entre la condición de ganador o perdedor, por lo que la hipótesis planteada se cumple en los catorce coeficientes de eficacia. A su vez, de los partidos femeninos podemos inferir que, en doce de los catorce coeficientes de eficacia existen diferencias significativas entre la condición de ganador o perdedor, por lo que la hipótesis planteada se cumple en el CCLDNTSCP, en el CDLDNTSCP, en el CPRLDNTSCP, en el CELDNTSCP, en el CCLDNTSSP, en el CDLDNTSSP, en el CPRLDNTSSP, en el CELDNTSSP, en el CPLDNTSCP, en el CPLDNTSSP, en el CRLDNTSCP y en el CRLDNTSSP.

    Si se quisiera hacer una transferencia de las conclusiones a las que se ha llegado, al entrenamiento de las microsituaciones de juego en desigualdad numérica temporal simple en waterpolo masculino, deberíamos tener en cuenta a la hora de programar las sesiones y partidos que, más que buscar los desplazamientos de los jugadores en superioridad numérica, hay que obligar a moverse a los jugadores en inferioridad, para tener la opción de finalizar con comodidad y poder acertar en la toma de decisión y exactitud en el lanzamiento. El medio para conseguir esa situación ventajosa debe ser a través de acciones de pases muy rápidos y precisos, fintando y de mano a mano. Además se debe establecer algunas secuencias de juego para, sin querer automatizar esta microsituación de juego, no dejarlo a la libre inspiración de algún jugador. Y por el contrario, se programarán tareas en las que el objetivo principal sea impedir acciones de pase cómodo, obligando en la medida de lo posible a que el jugador con posesión del balón deba enviarlo al compañero más alejado, con lo que se buscará la dificultad de ese pase y que el tiempo de exclusión finalice. En el caso del waterpolo femenino, además de lo anteriormente descrito, se debe aumentar el entrenamiento de los bloqueos de los lanzamientos, ya que puede permitir mejorar las posibilidades de victoria.

    En posteriores trabajos se podría abordar el estudio de las mismas variables con un mayor número de partidos y, especialmente, con las modificaciones reglamentarias propuestas por la FINA para el periodo 2005-09, sobre la defensa del lanzamiento fuera del área de 5 metros, comparando los datos obtenidos en ambos trabajos.

Referencias bibliográficas

• Anguera, M. T., et al. (2000). La metodología observacional en el deporte: conceptos básicos. Lecturas: Educación Física y Deportes, Revista Digital, 24. Extraído en octubre 5, 2004 disponible en: http://www.efdeportes.com.

• Anguera, M. T. (2003). Diseños observacionales en la actividad física y el deporte: estructura, alcance, y nuevas perspectivas. Ponencia presentada en el II Congreso Mundial de Ciencias de la Actividad Física y del Deporte, Granada, España.

• Argudo, F. (2000). Modelo de evaluación táctica en deportes de oposición con colaboración. Estudio práxico del waterpolo. Tesis Doctoral. Universitat de Valencia.

• Argudo, F. (2002). Táctica deportiva: entrenamiento, evaluación y planificación. En Programme du colloque de praxéologie motrice: "Motricités, savoirs et valeurs". Sorbonne, París, Francia.

• Argudo, F. (2005). Conceptos, contenidos y evaluación táctica en waterpolo. Apuntes personales sin publicar.

• Argudo, F., Alonso, J. I. & Fuentes, F. (2005). Computerized registration for tactical quantitative evaluation in water polo. Polo partido v1.0. Proceedings of the 5th International Symposium Computer Science in Sport. Croatia.

• Argudo, F. & Lloret, M. (2006). Investigación en waterpolo (1990-2003). Murcia: UCAM.

• Argudo, F. & Ruiz, E (2006). Validation of a tactical evaluation process in water polo. Proceedings of the 7th World Congress of Performance Analysis of Sport. Hungary.

• Argudo, F. & Ruiz, E (2006). Validation of an instrument for evaluation the goalkeeper in water polo. Proceedings of the 7th World Congress of Performance Analysis of Sport. Hungary.

• Canossa, S., Garganta, J. y Lloret, M. (2002). Estudo do processo ofensivo em selecções femininas de polo aquático participantes no campeonato europeu de Sevilha 1997. Estudos 3 - CEFD. Porto: FCDEF-UP.

• Dopsaj, M. & Matkovic, I. (1999). The structure of technical and tactical activities of water polo players in the First Yugoslav League during the game. In Biomechanics and medicine in Swimming. Proceedings of the VIII International Symposium on Biomechanics and Medicine in Swimming, University of Jyvaskyla, Department of Biology of Physical Activity, Finland.

• Enomoto, I. (2004). A Notational Match Analysis of the 2001 Women´s Water Polo World Championships. World Congress of Performance Analysis in Sports, 6. Belfast, Northen Ireland.

• Gayoso, F. (1983). Fundamentos de táctica deportiva. Madrid: Gayoso, F. Ed.

• Lloret, M. (1994). Análisis de la acción de juego en el waterpolo durante la Olimpiada de 1992. Tesis Doctoral. Universidad de Barcelona.

• Lloret, M. (1995). Análisis praxiológico del waterpolo. Revista de Entrenamiento Deportivo, VIII(2), 28-36.

• Lloret, M. (1999). Los coeficientes ofensivos y defensivos, una aportación al estudio práxico de los deportes de equipo. Apunts, 55, 68-76.

• Majoni, M. (1954). Pallanuoto. Milano: Sterling and Kupfer.

• Platanou, T. (2001). Time motion assessment in highly competitive water polo players. Proceedings of the 6th Annual Congress of the European College of Sport Science, German Society of Sport Science, Germany, 552.

• Platanou, T. (2004). Analysis of the extra man in water polo: a comparison between winning and losing teams and players of different playing position. Journal of Human Movement Studies, 46, 205-211.

• Sarmento, J. (1991). Análise das acçoes ofensivas. Horizonte, 45(7), 88-91.

• Sarmento, J. & Magalhaes, L. (1991). Determinaçao de coeficientes para a valorizaçao da observaçao do ataque em pólo aquático. Nataçao, 13(4), 7-8.

	Web EFDeportes.com
revista digital · Año 12 · N° 114 | Buenos Aires, Noviembre 2007   © 1997-2007 Derechos reservados