1 / 1

Introducción

    Las exigencias del requerimiento físico en balonmano vienen marcadas por el tipo de acciones que se presentan. La mayoría de ellas son intervenciones de corta duración y de gran intensidad. Casi el 25% del total del partido corresponde a acciones de potencia, relacionadas con distintas formas de desplazamiento, cambios de velocidad, saltos, contactos, lanzamientos, etc.

    Hemos diseñado una serie de test que nos van a permitir valorar la fuerza útil de los lanzamientos de balonmano. Dichos valores nos van a permitir valorar y depurar los programas de entrenamiento de fuerza en balonmano.

Material y métodos

Características generales de los Ergodinamómetros^1,2

    En general, el Ergodinamómetro consta de una serie de elementos electromagnéticos encargados de medir y registrar la fuerza desarrollada por un grupo muscular aislado, o bien de una cadena cinética específica.

Descripción del Ergodinamómetro

    A diferencia de otros sistemas de medición, nuestro Ergodinamómetros ha sido diseñado específicamente para la valoración y estudio de la fuerza y velocidad de un gesto técnico concreto, aplicado a la práctica deportiva, con la particularidad de que no existe limitación del eje en que se realiza dicho gesto deportivo.

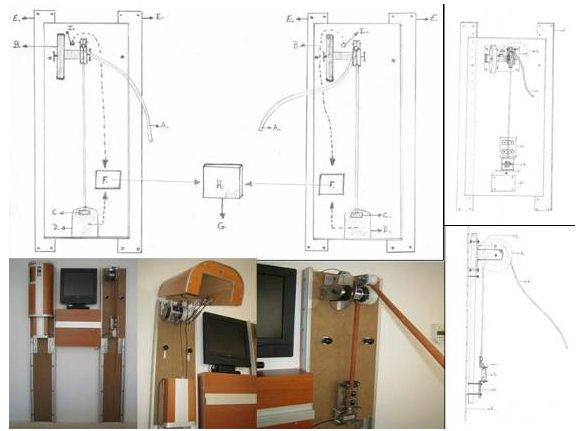
    Ello es posible mediante la utilización de un complejo sistema de medición electromecánico, capaz de registrar las variables físicas generadas en un elemento elástico sobre el que actúan un sujeto durante todo el tiempo de ejecución de ese gesto técnico específico.

Características del Ergodinamómetro

    El Ergodinamómetro esta constituido por un elemento elástico montado sobre un sistema de poleas que trasmite la fuerza generada durante la realización del gesto técnico a un disco ( de una masa de 500 gr.) imprimiéndole velocidad de giro en el proporcional a la tensión generada en el dicho elemento elástico.

    Dicha velocidad de giro del disco dependerá del tiempo y de la fuerza empleados en la realización del gesto, así como del tiempo empleado en la fase de relajación del ejercicio.

    Así pues, cuanta mayor tensión se realiza en el elemento elástico en el menor tiempo posible, y/o cuanto menor sea el tiempo y mayor la velocidad de relajación tras la fuerza generada, mayor velocidad de giro del disco obtendremos.

    Para medir la fuerza generada durante el gesto, el Ergodinamómetro dispone de un sensor calibrado con el elemento elástico. Tanto los datos generados en el disco durante su rotación (revoluciones por minuto; pendiente de la velocidad del disco desde la posición de reposo; variaciones de la velocidad de giro del disco en el tiempo del transcurso del gesto técnico, etc.), como en el sensor de tensión, son trasmitidos y posteriormente analizados por un sistema informático que procesa todas las fases de la ejecución del gesto técnico.

    Para maximizar la precisión, tanto el sistema de poleas y el disco, como el sensor de la fuerza, están montados sobre un adaptador antropométrico que permite ajustar el ergodinamómetro a las características antropométricas del sujeto estudiado.

Resultados

    Vamos a describir las curvas obtenidas tras la realización de 4 lanzamientos de balonmano, analizando tanto la curva fuerza-tiempo como velocidad del disco-tiempo.

1. Descripción del movimiento de lanzamiento en apoyo clásico a la altura del hombro del brazo ejecutor

Descripción del test

1º Fase de preparación

    El lanzador debe colocarse con la pierna contraria al brazo ejecutor ligeramente adelantada. El brazo ejecutor debe colocarse en posición horizontal y semiflexionado, de manera que el antebrazo está orientado verticalmente, formando entre ambos segmentos corporales un ángulo recto. La cara palmar está dirigida hacia la dirección del supuesto lanzamiento y los dedos están orientados hacia arriba. El tronco tiene una ligera rotación hacia el lado del brazo ejecutor.

2º Fase de ejecución

    El lanzamiento se produce mediante la rotación del tronco en el sentido del movimiento, pasando el peso del cuerpo desde la pierna atrasada (la derecha) hacia la pierna adelantada (la izquierda) y realizando un movimiento del brazo de atrás a hacia delante y de arriba abajo.

3º Fase de relajación

    La parte final del movimiento se completa con el movimiento del brazo ejecutor de forma que cruza el cuerpo y posteriormente recuperamos la posición inicial.

Estudio de las curvas

    Tras la realización del test, vamos a obtener las dos variables estudiadas, La fuerza recogida en la célula de carga y la inercia, recogida en el volante de inercia. Para analizar estas secuencias de datos, se van a representar en función del tiempo.

    Por tanto tras la realización del test, obtendremos dos curvas:

1. La curva fuerza-tiempo. Esta curva va a describir la evolución de la fuerza durante el Clear. Dicha curva se va a iniciar con un ascenso que corresponderá a la fase de ejecución del golpeo, seguido de un descenso que representara la fase de relajación. Dicha curva va a ser la representación o huella de la fuerza útil del gesto técnico.

2. La curva velocidad del disco-tiempo. Esta curva representa el impulso aplicado sobre el disco, y probablemente, la eficiencia conseguida con el gesto técnico.

    Dichas curvas si bien están correlacionadas, no siguen una distribución paralela, consiguiéndose a iguales valores de fuerza, distintos valores de eficiencia, y viceversa.

Análisis numérico de la curva fuerza-tiempo

    La primera curva que vamos a analizar será la referida a la curva fuerza- tiempo, dicha curva se obtiene del cálculo informático y previamente automatizado de todos los valores obtenidos por la célula de carga al ser ordenados en función del tiempo.

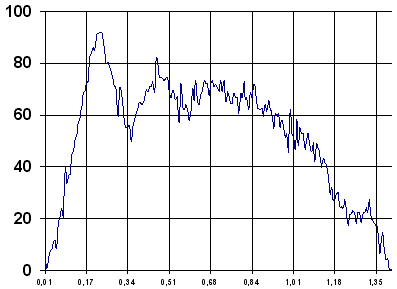
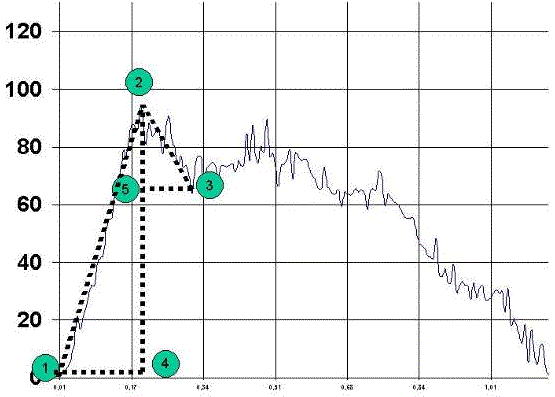
    Para el análisis de esta curva, vamos a definir 5 puntos:

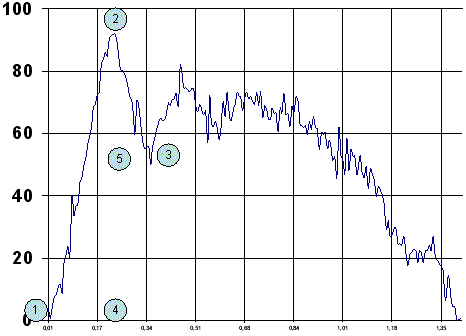
    1º punto, donde se inicia la curva. Se mide en centésimas de segundos. Dicho valor se denomina Punto de Arranque.

    2º punto, de fuerza máxima. Se mide en Newton y se denomina (siguiendo la literatura) Pico de Fuerza máxima.

    3º punto, donde acaba la fase de relajación de la curva. Se mide en centésimas de segundos. Dicho punto se denomina Punto Final.

    4º punto, tiempo en que se alcanza la fuerza máxima. Se mide en centésimas de segundos y se denomina Tiempo de Pico de Fuerza Máxima.

    5º punto, representa el punto sobre el cual se realizara el cateto inferior del triangulo de relajación se coloca en la perpendicular de la línea imaginaria que une el punto 2 y el punto 4 a la altura marcada por una línea imaginaria que cruza esta línea al nivel del punto 3., se mide en centésimas de segundo y se denomina, Punto inicial del tiempo de relajación

    Lógicamente los mejores resultados se obtendrán cuando el deportista en su evolución desplace la curva hacia la izquierda y hacia arriba. Obteniendo más fuerza en menos tiempo, y los resultados negativos cuando la curva se desplace hacia la derecha y abajo, es decir menos fuerza en más tiempo.

    Del análisis de estos puntos del lanzamiento, podemos definir 2 triángulos.

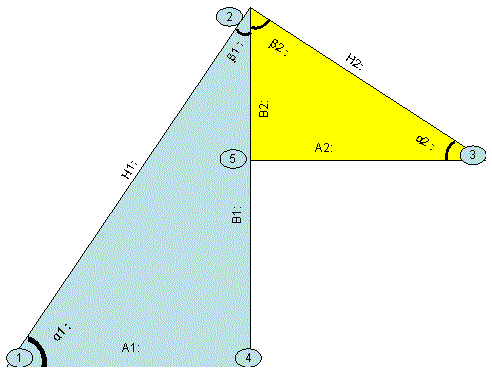
    El triángulo situado a la izquierda se denominara triangulo de aceleración, mientras que el triangulo situado a la derecha de denominara triangulo de relajación.

    En dichos triángulos vamos a definir los siguientes valores:

A1: Si unimos el punto 1 y el punto 4 obtenemos el valor del tiempo que el deportista tarda en alcanzar el máximo, Aunque este valor se dibuje gráficamente en centésimas de segundos a la hora de tratar los datos numéricamente de debe de referir en segundos. Dicho valor se denomina: Tiempo de aceleración

A2: Si unimos el punto 5 y el punto 3, obtenemos el valor del tiempo que el deportista tarda en relajarse del golpeo. Aunque este valor se dibuje gráficamente en centésimas de segundos, a la hora de tratar los datos numéricamente de debe de referir en segundos. Dicho valor se denomina: Tiempo de relajación

B1: Si unimos el punto 2 y el punto 4, obtenemos el valor de la fuerza máxima alcanzada por el deportista, dicho valor se mide en Newton y se denomina: Pico de Fuerza Máxima

B2: Si unimos el punto 2 y el punto 5, obtenemos el valor de la pérdida de fuerza alcanzada por el deportista en la fase de relajación, dicho valor se mide en Newton y se denomina: Perdida de Fuerza Máxima.

H1: Si unimos el punto 1 y el punto 2, obtenemos el valor de la hipotenusa ascendente, para hacerlos debemos de aplicar el teorema de Pitágoras que dice que H1²= A1²+B², por tanto H1=A1²+B². Dicho valor se denomina hipotenusa de Aceleración.

FE: Para valorar la fuerza explosiva tradicionalmente se ha relacionado la fuerza máxima con el tiempo tardado en producirla. Así en nuestra curva la fuerza explosiva seria la relación existente entre B y A1, siguiendo la formula⁽³⁾:

Fuerza explosiva (N*s^-1) = Fuerza máxima (N)/ Tiempo de aceleración (s)

Alfa 1: ángulo que muestra la pendiente del grafico y se calcula mediante la siguiente fórmula Alfa 1=cos^-1 (A1/H1). Se mide en grados. Dicho ángulo se denomina Angulo de aceleración.

Beta 1: Angulo que cierra el triangulo se calcula mediante la formula Beta1= 90-alfa1. Se mide en grados. Dicho ángulo se denomina, Angulo complementario de aceleración

H2: Si unimos el punto 2 y el punto 3, obtenemos el valor de la hipotenusa descendente. Para hacerlo debemos aplicar el teorema de Pitágoras, que dice que H2²= A2²+B², por tanto H2= A2²+B². Dicho valor se denomina hipotenusa de relajación

Alfa 2: ángulo que muestra la pendiente del grafico y se calcula mediante la siguiente fórmula Alfa 2=cos^-1 (A2/H2). Se mide en grados. Dicho ángulo se denomina ángulo complementario de relajación.

Beta 2: Angulo que cierra el triangulo. Se calcula mediante la fórmula Beta2= 90-Alfa2. Se mide en grados. Dicho ángulo se denomina ángulo de relajación

Angulo superior: Se obtiene de la suma de los dos ángulo Beta (ángulos complementarios de aceleración y relajación respectivamente). Mediante la formula Angulo superior= Beta 1 + Beta 2. Se mide en grados. Dicho ángulo marca la transición entre la aceleración y la relajación.

Análisis cualitativo de la curva de fuerza-tiempo

    Además del análisis de la curva Fuerza-Tiempo de una manera cuantitativa, debemos analizar la huella de la grafica, dicha huella se analizara de una manera cualitativa, basándose en el análisis consecutivo e individualizado de las siguientes variables.

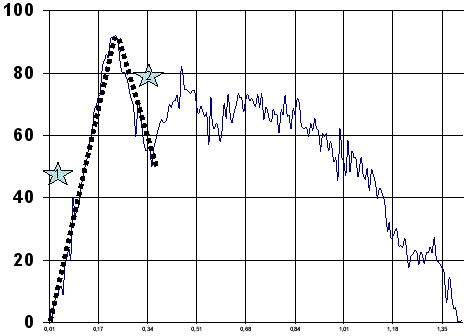
    Definimos 2 secciones a la hora de definir cualitativamente.

    En la fase de aceleración denominada Zona número 1 por tanto, que corresponderá a la hipotenusa del análisis numérico. Estará situada ente los puntos 1 y 2 del gráfico numérico. En dicho zona gráfica se debe valorar tanto la pendiente, que luego se valorara numéricamente con el ángulo alfa 1, como la cualidad de dicho trazado, así como si tiene varios ángulos intermedios en la pendiente. Dicha zona se denomina: Zona de aceleración

    En la fase de relajación o deceleración denominada zona numero 2 del grafico, correspondería a la zona de relajación. Estará situada entre los puntos 3 y 3 del grafico numérico. Deberá valora tanto la pendiente como la profundidad de la misma. Dicho valor se denomina: Zona de relajación.

Valoración cualitativa de la curva velocidad del disco-tiempo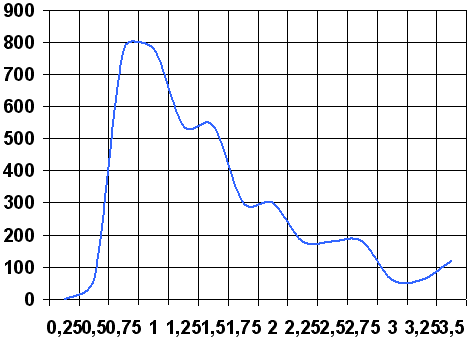

    Para la valoración de la eficiencia del gesto técnico nos vamos a basar en la curva Velocidad del disco-Tiempo (rpm/s). Dicha velocidad refleja la velocidad que el gesto técnico le imprime al volante. Los valores son registrados cada 0.25 segundos y la curva que vamos a analizar surge de la representación de estos valores con respecto al tiempo.

    Para el análisis de la curva velocidad del disco-tiempo vamos a definir de nuevo cuatro puntos:

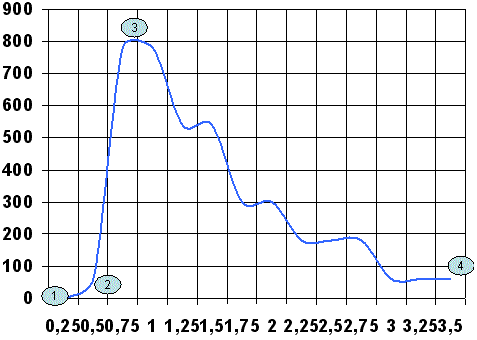
Punto 1: Es el origen de la medición de velocidad. Se mide en revoluciones por minuto. Se denomina Punto de aceleración Inicial.

Punto 2: En muchos casos encontramos un segundo punto de aceleración o de inflexión de la curva. Se mide en revoluciones por minuto. Se denomina, punto de aceleración secundario. Si el impulso es lo suficientemente potente, dicho punto puede desaparecer.

Punto 3: Se alcanza el valor máximo de velocidad. Se mide en revoluciones por minuto, Se denomina Punto de Máxima Velocidad.

Punto 4: Es el final de la curva. Se mide en revoluciones por minuto. Se denomina Punto de desaceleración.

    Del análisis de estos 4 puntos obtenemos 6 variables cuantitativas:

Z1 vel: Valor de la velocidad en revoluciones por minuto en el punto 2 o punto de aceleración secundario. Se denomina velocidad de arrancada. Dicho punto puede no aparecer si la zona de arrancada es asumida dentro de la zona de aceleración.

Z1 Ti: Valor en segundos de la zona de arrancada. Es decir tiempo que trascurre entre el punto 1 (punto de aceleración inicial) y el punto 2 (punto de aceleración secundario). Se denomina tiempo de arrancada. Dicho tiempo puede no aparecer si la zona de arrancada es asumida dentro de la zona de aceleración.

Z2 vel: Valor de la velocidad en revoluciones por minuto en el punto 3 o punto de Máxima Velocidad. Se denomina velocidad máxima.

Z2 Ti: Valor en segundos de la zona de aceleración. Es decir en tiempo que trascurre entre el punto 1 (punto de aceleración inicial) y el punto 3 ( Punto de Máxima Velocidad). Se denomina tiempo de velocidad máxima

Z3 Vel: Valor de la velocidad en el revoluciones por minuto en el punto 4 o punto de deceleración. Se denomina velocidad final.

Z3 Ti: Valor en segundos de la zona de deceleración. Es decir el tiempo que trascurre entre el punto 3 (punto de Máxima Velocidad) y el punto 4 ( Punto de deceleración). Se denomina Tiempo de deceleración.

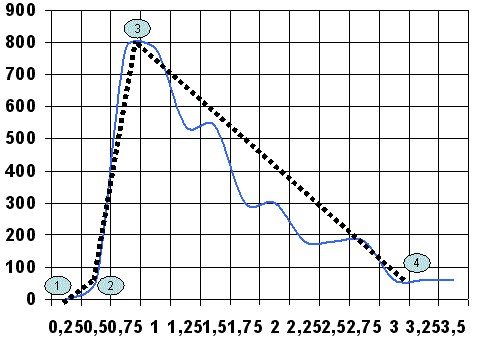
    Si analizamos cualitativamente las curvas velocidad-tiempo. Definimos tres zonas:

    La primera zona es la zona de aceleración inicial, y es la que va desde el punto 1 al punto 2, pudiendo variar tanto en pendiente como en longitud. Dicho valor se denomina: Zona de arrancada. Esta zona puede quedar englobada dentro de la zona de aceleración y no ser valorable.

    La segunda zona va desde el punto 2 al punto 3, y varía al igual que el anterior en pendiente y en longitud. Dicho valor se denomina: Zona de aceleración.

    La tercera zona va desde el punto 3 al punto 4 y varia igual que el anterior en pendiente y longitud. Dicho valor se denomina: Zona de deceleración.

2. Descripción del movimiento de lanzamiento en apoyo clásico a la altura intermedia del brazo ejecutor

Descripción del test

1º Fase de preparación

    El lanzador debe colocarse con la pierna contraria al brazo ejecutor ligeramente adelantada. El brazo ejecutor debe colocarse en posición horizontal y el antebrazo también estará colocado en la misma posición, con el borde radial hacia arriba, de manera que prácticamente estén paralelos al suelo, contando con una ligera flexión del codo. La cara palmar está dirigida hacia la dirección del lanzamiento y los dedos están orientados lateralmente. El tronco tiene una ligera rotación e inclinación hacia el lado del brazo ejecutor.

2º Fase de ejecución

    El lanzamiento se produce mediante la rotación del tronco en el sentido del movimiento, pasando el peso del cuerpo desde la pierna atrasada (la derecha) hacia la pierna adelantada (la izquierda) y realizando un movimiento del brazo de atrás a hacia delante.

3º Fase de relajación

    La parte final del movimiento se completa con el movimiento del brazo ejecutor de forma que cruza el cuerpo y posteriormente recuperamos la posición inicial.

Estudio de las curvas

    Tras la realización del test, vamos a obtener las dos variables estudiadas, La fuerza recogida en la célula de carga y la inercia, recogida en el volante de inercia. Para analizar estas secuencias de datos, se van a representar en función del tiempo.

    Por tanto tras la realización del test, obtendremos dos curvas:

1. La curva fuerza-tiempo: esta curva va a describir la evolución de la fuerza durante el Clear. Dicha curva se va a iniciar con un ascenso que corresponderá a la fase de ejecución del golpeo, seguido de un descenso que representara la fase de relajación. Dicha curva va a ser la representación o huella de la fuerza útil del gesto técnico.

2. La curva velocidad del disco-tiempo. Esta curva representa el impulso aplicado sobre el disco, y probablemente, la eficiencia conseguida con el gesto técnico.

    Dichas curvas si bien están correlacionadas, no siguen una distribución paralela, consiguiéndose a iguales valores de fuerza, distintos valores de eficiencia, y viceversa.

Análisis numérico de la curva fuerza-tiempo

    La primera curva que vamos a analizar será la referida a la curva fuerza- tiempo, dicha curva se obtiene del cálculo informático y previamente automatizado de todos los valores obtenidos por la célula de carga al ser ordenados en función del tiempo.

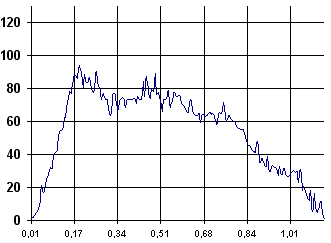
    Para el análisis de esta curva, vamos a definir 4 puntos:

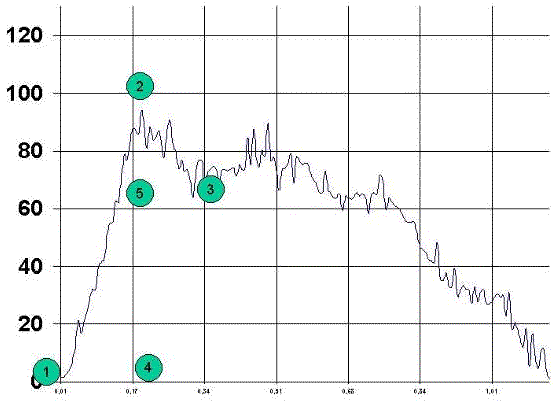
1º punto, donde se inicia la curva. Se mide en centésimas de segundos. Dicho valor se denomina Punto de Arranque.

2º punto, de fuerza máxima. Se mide en Newton y se denomina -siguiendo la literatura, Pico de Fuerza máxima.

3º punto, donde acaba la fase de relajación. Se mide en centésimas de segundos. Dicho punto se denomina Punto Final.

4º punto, tiempo en que se alcanza la fuerza máxima. Se mide en centésimas de segundos y se denomina Tiempo de Pico de Fuerza Máxima.

5º punto, representa el punto sobre el cual se realizara el cateto inferior del triangulo de relajación se coloca en la perpendicular de la línea imaginaria que une el punto 2 y el punto 4 a la altura marcada por una línea imaginaria que cruza esta línea al nivel del punto 3., se mide en centésimas de segundo y se denomina, Punto inicial del tiempo de relajación

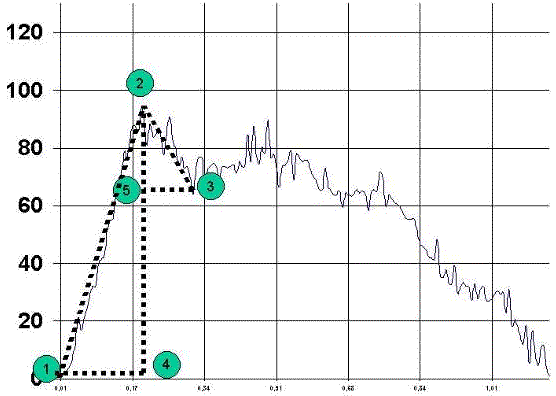
    Lógicamente los mejores resultados se obtendrán cuando el deportista en su evolución desplace la curva hacia la izquierda y hacia arriba. Obteniendo más fuerza en menos tiempo, y los resultados negativos cuando la curva se desplace hacia la derecha y abajo, es decir menos fuerza en más tiempo.

    Del análisis de estos puntos del lanzamiento, podemos definir 2 triángulos.

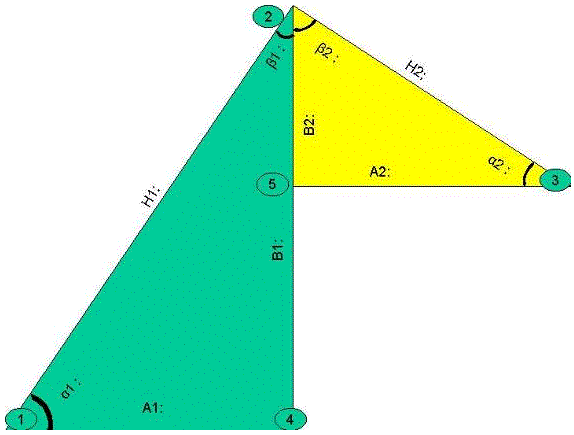
    El triángulo situado a la izquierda se denominara triangulo de aceleración, mientras que el triangulo situado a la derecha de denominara triangulo de relajación.

    En dichos triángulos vamos a definir los siguientes valores:

A1: Si unimos el punto 1 y el punto 4 obtenemos el valor del tiempo que el deportista tarda en alcanzar el máximo, Aunque este valor se dibuje gráficamente en centésimas de segundos a la hora de tratar los datos numéricamente de debe de referir en segundos. Dicho valor se denomina: Tiempo de aceleración

A2: Si unimos el punto 5 y el punto 3, obtenemos el valor del tiempo que el deportista tarda en relajarse del golpeo. Aunque este valor se dibuje gráficamente en centésimas de segundos, a la hora de tratar los datos numéricamente de debe de referir en segundos. Dicho valor se denomina: Tiempo de relajación

B1: Si unimos el punto 2 y el punto 4, obtenemos el valor de la fuerza máxima alcanzada por el deportista, dicho valor se mide en Newton y se denomina: Pico de Fuerza Máxima

B2: Si unimos el punto 2 y el punto 5, obtenemos el valor de la pérdida de fuerza alcanzada por el deportista en la fase de relajación, dicho valor se mide en Newton y se denomina: Perdida de Fuerza Máxima.

H1: Si unimos el punto 1 y el punto 2, obtenemos el valor de la hipotenusa ascendente, para hacerlos debemos de aplicar el teorema de Pitágoras que dice que H1²= A1²+B², por tanto H1= A1²+B². Dicho valor se denomina hipotenusa de Aceleración.

FE: Para valorar la fuerza explosiva tradicionalmente se ha relacionado la fuerza máxima con el tiempo tardado en producirla. Así en nuestra curva la fuerza explosiva seria la relación existente entre B y A1, siguiendo la formula⁽³⁾:

Fuerza explosiva (N*s^-1) = Fuerza máxima (N)/ Tiempo de aceleración (s)

Alfa 1: ángulo que muestra la pendiente del grafico y se calcula mediante la siguiente fórmula Alfa 1=cos^-1 (A1/H1). Se mide en grados. Dicho ángulo se denomina Angulo de aceleración.

Beta 1: Angulo que cierra el triangulo se calcula mediante la formula Beta1= 90-alfa1. Se mide en grados. Dicho ángulo se denomina, Angulo complementario de la aceleración

H2: Si unimos el punto 2 y el punto 3, obtenemos el valor de la hipotenusa descendente. Para hacerlo debemos aplicar el teorema de Pitágoras, que dice que H2²= A2²+B², por tanto H2= A2²+B². Dicho valor se denomina hipotenusa de relajación

Alfa 2: ángulo que muestra la pendiente del grafico y se calcula mediante la siguiente fórmula Alfa 2=cos^-1 (A2/H2). Se mide en grados. Dicho ángulo se denomina ángulo complementario de relajación.

Beta 2: Angulo que cierra el triangulo. Se calcula mediante la fórmula Beta2= 90-alfa2. Se mide en grados. Dicho ángulo se denomina ángulo de relajación

Angulo superior: Se obtiene de la suma de los dos ángulo Beta (ángulos complementarios de aceleración y relajación respectivamente). Mediante la formula Angulo superior= Beta 1 + Beta 2. Se mide en grados. Dicho ángulo marca la transición entre la aceleración y la relajación.

Análisis cualitativo de la curva de fuerza-tiempo

    Además del análisis de la curva Fuerza-Tiempo de una manera cuantitativa, debemos analizar la huella de la grafica, dicha huella se analizara de una manera cualitativa, basándose en el análisis consecutivo e individualizado de las siguientes variables.

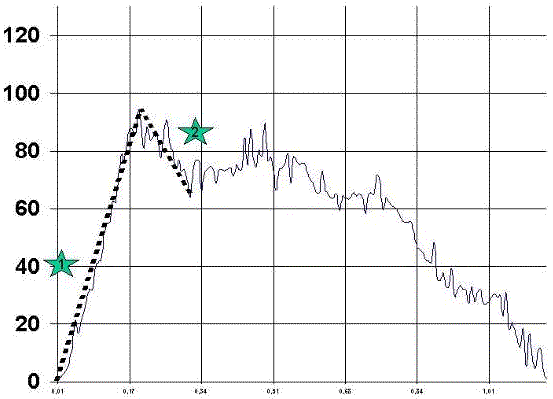
    Definimos 2 secciones a la hora de definir cualitativamente.

    En la fase de aceleración denominada Zona número 1 por tanto, que corresponderá a la hipotenusa del análisis numérico. Estará situada ente los puntos 1 y 2 del gráfico numérico. En dicho zona gráfica se debe valorar tanto la pendiente, que luego se valorara numéricamente con el ángulo alfa 1, como la cualidad de dicho trazado, así como si tiene varios ángulos intermedios en la pendiente. Dicha zona se denomina: Zona de aceleración

    En la fase de relajación o deceleración denominada zona numero 2 del grafico, correspondería a la zona de relajación y se deberá valorar tanto la pendiente como la profundidad de la misma. Dicho valor se denomina: Zona de relajación.

Valoración cualitativa de la curva velocidad del disco-tiempo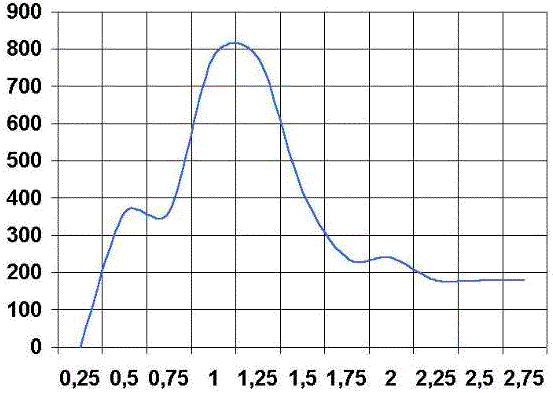

    Para la valoración de la eficiencia del gesto técnico nos vamos a basar en la curva Velocidad del disco-Tiempo (rpm/s). Dicha velocidad refleja la velocidad que el gesto técnico le imprime al volante. Los valores son registrados cada 0.25 segundos y la curva que vamos a analizar surge de la representación de estos valores con respecto al tiempo.

    Para el análisis de la curva velocidad del disco-tiempo vamos a definir de nuevo cuatro puntos:

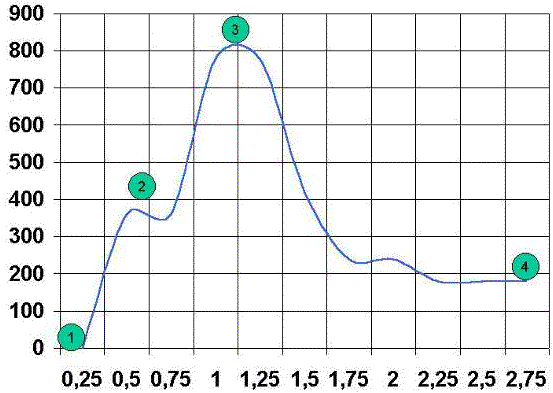
Punto 1: Es el origen de la medición de velocidad. Se mide en revoluciones por minuto. Se denomina Punto de aceleración Inicial.

Punto 2: En muchos casos encontramos un segundo punto de aceleración o de inflexión de la curva. Se mide en revoluciones por minuto. Se denomina, punto de aceleración secundario. Si el impulso es lo suficientemente potente, dicho punto puede desaparecer.

Punto 3: Se alcanza el valor máximo de velocidad. Se mide en revoluciones por minuto, Se denomina Punto de Máxima Velocidad.

Punto 4: Es el final de la curva. Se mide en revoluciones por minuto. Se denomina Punto de deceleración.

    Del análisis de estos 4 puntos obtenemos 6 variables cuantitativas:

Z1 vel: Valor de la velocidad en revoluciones por minuto en el punto 2 o punto de aceleración secundario. Se denomina velocidad de arrancada. Dicho punto puede no aparecer si la zona de arrancada es asumida dentro de la zona de aceleración.

Z1 Ti: Valor en segundos de la zona de arrancada. Es decir tiempo que trascurre entre el punto 1 (punto de aceleración inicial) y el punto 2 (punto de aceleración secundario). Se denomina tiempo de arrancada. Dicho tiempo puede no aparecer si la zona de arrancada es asumida dentro de la zona de aceleración.

Z2 vel: Valor de la velocidad en revoluciones por minuto en el punto 3 o punto de Máxima Velocidad. Se denomina velocidad máxima.

Z2 Ti: Valor en segundos de la zona de aceleración. Es decir en tiempo que trascurre entre el punto 1 (punto de aceleración inicial) y el punto 3 (Punto de Máxima Velocidad). Se denomina tiempo de velocidad máxima

Z3 Vel: Valor de la velocidad en el revoluciones por minuto en el punto 4 o punto de deceleración. Se denomina velocidad final.

Z3 Ti: Valor en segundos de la zona de deceleración. Es decir el tiempo que trascurre entre el punto 3 (punto de Máxima Velocidad) y el punto 4 (Punto de deceleración). Se denomina Tiempo de deceleración.

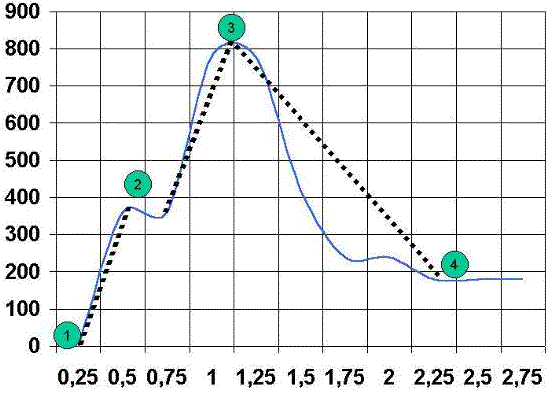
    Si analizamos cualitativamente las curvas velocidad-tiempo. Definimos tres zonas:

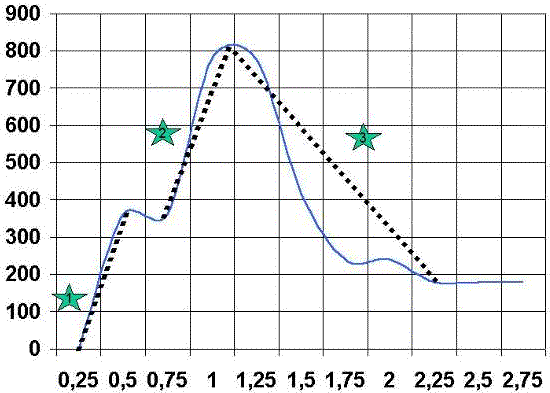
    La primera zona es la zona de aceleración inicial, y es la que va desde el punto 1 al punto 2, pudiendo variar tanto en pendiente como en longitud. Dicho valor se denomina: Zona de arrancada.

    La segunda zona va desde el punto 2 al punto 3, y varía al igual que el anterior en pendiente y en longitud. Dicho valor se denomina: Zona de aceleración.

    La tercera zona va desde el punto 3 al punto 4 y varia igual que el anterior en pendiente y longitud. Dicho valor se denomina: Zona de deceleración.

3. Descripción del movimiento de lanzamiento en apoyo clásico a la altura del hombro del brazo ejecutor con ciclo de pasos

Descripción del test

1º Fase de preparación

    El lanzador debe colocarse con los pies ligeramente separados y colocados simétricamente y con ambas manos a la altura de la cadera.

2º Fase de ejecución

    Se inicia el ciclo de pasos con la pierna contraria al brazo ejecutor, dándose los tres pasos posibles. Durante la ejecución del último paso se realiza el armado de brazo, con una sola mano. El brazo ejecutor debe colocarse en posición horizontal y semiflexionado, de manera que el antebrazo está orientado verticalmente, formando entre ambos segmentos corporales un ángulo recto. La cara palmar está dirigida hacia la dirección del lanzamiento y los dedos están orientados hacia arriba. El tronco tiene una ligera rotación hacia el lado del brazo ejecutor.

    Cuando finaliza el último paso se produce el lanzamiento iniciándose la rotación del tronco en el sentido del movimiento, pasando el peso del cuerpo desde la pierna atrasada (la derecha) hacia la pierna adelantada (la izquierda) y realizando un movimiento del brazo de atrás a hacia delante y de arriba abajo.

3º Fase de relajación

    La parte final del movimiento se completa con el movimiento del brazo ejecutor de forma que cruza el cuerpo y posteriormente recuperamos la posición inicial.

Estudio de las curvas

    Tras la realización del test, vamos a obtener las dos variables estudiadas, La fuerza recogida en la célula de carga y la inercia, recogida en el volante de inercia. Para analizar estas secuencias de datos, se van a representar en función del tiempo.

    Por tanto tras la realización del test, obtendremos dos curvas:

1. La curva fuerza-tiempo: esta curva va a describir la evolución de la fuerza durante el Clear. Dicha curva se va a iniciar con un ascenso que corresponderá a la fase de ejecución del golpeo, seguido de un descenso que representara la fase de relajación. Dicha curva va a ser la representación o huella de la fuerza útil del gesto técnico.

2. La curva velocidad del disco-tiempo. Esta curva representa el impulso aplicado sobre el disco, y probablemente, la eficiencia conseguida con el gesto técnico.

    Dichas curvas si bien están correlacionadas, no siguen una distribución paralela, consiguiéndose a iguales valores de fuerza, distintos valores de eficiencia, y viceversa.

Análisis numérico de la curva fuerza-tiempo

    La primera curva que vamos a analizar será la referida a la curva fuerza- tiempo, dicha curva se obtiene del cálculo informático y previamente automatizado de todos los valores obtenidos por la célula de carga al ser ordenados en función del tiempo.

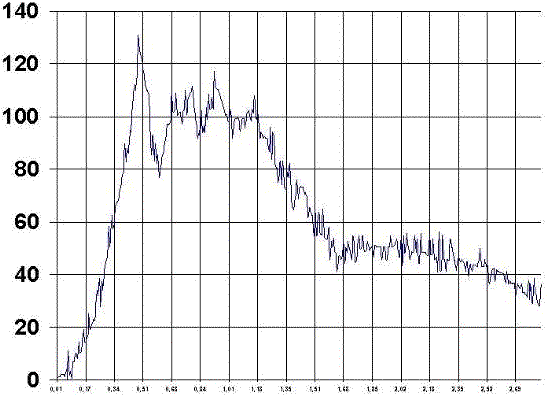
    Para el análisis de esta curva, vamos a definir 4 puntos:

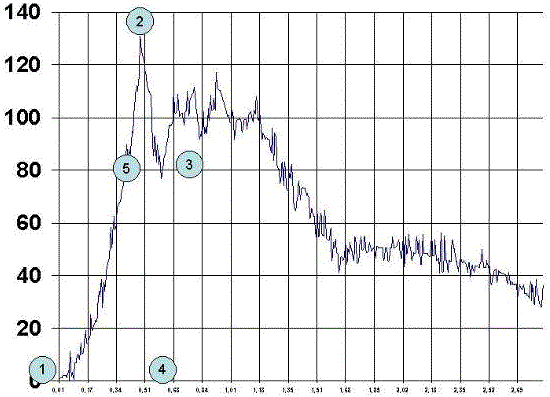
1º punto, donde se inicia la curva. Se mide en centésimas de segundos. Dicho valor se denomina Punto de Arranque.

2º punto, de fuerza máxima. Se mide en Newton y se denomina -siguiendo la literatura, Pico de Fuerza máxima.

3º punto, donde acaba la curva. Se mide en centésimas de segundos. Dicho punto se denomina Punto Final.

4º punto, tiempo en que se alcanza la fuerza máxima. Se mide en centésimas de segundos y se denomina Tiempo de Pico de Fuerza Máxima.

5º punto, representa el punto sobre el cual se realizara el cateto inferior del triangulo de relajación se coloca en la perpendicular de la línea imaginaria que une el punto 2 y el punto 4 a la altura marcada por una línea imaginaria que cruza esta línea al nivel del punto 3., se mide en centésimas de segundo y se denomina, Punto inicial del tiempo de relajación

     Lógicamente los mejores resultados se obtendrán cuando el deportista en su evolución desplace la curva hacia la izquierda y hacia arriba. Obteniendo más fuerza en menos tiempo, y los resultados negativos cuando la curva se desplace hacia la derecha y abajo, es decir menos fuerza en más tiempo.

    Del análisis de estos puntos del lanzamiento, podemos definir 2 triángulos.

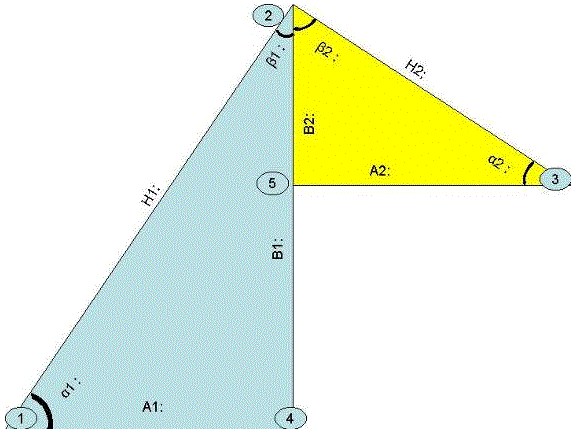
    El triángulo situado a la izquierda se denominara triangulo de aceleración, mientras que el triangulo situado a la derecha de denominara triangulo de relajación.

    En dichos triángulos vamos a definir los siguientes valores:

A1: Si unimos el punto 1 y el punto 4 obtenemos el valor del tiempo que el deportista tarda en alcanzar el máximo, Aunque este valor se dibuje gráficamente en centésimas de segundos a la hora de tratar los datos numéricamente de debe de referir en segundos. Dicho valor se denomina: Tiempo de aceleración

A2: Si unimos el punto 5 y el punto 3, obtenemos el valor del tiempo que el deportista tarda en relajarse del golpeo. Aunque este valor se dibuje gráficamente en centésimas de segundos, a la hora de tratar los datos numéricamente de debe de referir en segundos. Dicho valor se denomina: Tiempo de relajación

B1: Si unimos el punto 2 y el punto 4, obtenemos el valor de la fuerza máxima alcanzada por el deportista, dicho valor se mide en Newton y se denomina: Pico de Fuerza Máxima

B2: Si unimos el punto 2 y el punto 5, obtenemos el valor de la pérdida de fuerza alcanzada por el deportista en la fase de relajación, dicho valor se mide en Newton y se denomina: Perdida de Fuerza Máxima.

H1: Si unimos el punto 1 y el punto 2, obtenemos el valor de la hipotenusa ascendente, para hacerlos debemos de aplicar el teorema de Pitágoras que dice que H1²= A1²+B², por tanto H1= A1²+B². Dicho valor se denomina hipotenusa de Aceleración.

FE: Para valorar la fuerza explosiva tradicionalmente se ha relacionado la fuerza máxima con el tiempo tardado en producirla. Así en nuestra curva la fuerza explosiva seria la relación existente entre B y A1, siguiendo la formula⁽³⁾:

Fuerza explosiva (N*s^-1) = Fuerza máxima (N)/ Tiempo de aceleración (s)

Alfa 1: ángulo que muestra la pendiente del grafico y se calcula mediante la siguiente fórmula Alfa 1=cos^-1 (A1/H1). Se mide en grados. Dicho ángulo se denomina Angulo de aceleración.

Beta 1: Angulo que cierra el triangulo se calcula mediante la formula Beta1=90-alfa1. Se mide en grados. Dicho ángulo se denomina, Angulo complementario de la aceleración

H2: Si unimos el punto 2 y el punto 3, obtenemos el valor de la hipotenusa descendente. Para hacerlo debemos aplicar el teorema de Pitágoras, que dice que H2²= A2²+B², por tanto H2= A2²+B². Dicho valor se denomina hipotenusa de relajación

Alfa 2: ángulo que muestra la pendiente del grafico y se calcula mediante la siguiente fórmula Alfa 2=cos^-1 (A2/H2). Se mide en grados. Dicho ángulo se denomina ángulo complementario de relajación.

Beta 2: Angulo que cierra el triangulo. Se calcula mediante la fórmula Beta2=90-alfa2. Se mide en grados. Dicho ángulo se denomina ángulo de relajación

Angulo superior: Se obtiene de la suma de los dos ángulo Beta (ángulos complementarios de aceleración y relajación respectivamente). Mediante la formula Angulo superior= Beta 1 + Beta 2. Se mide en grados. Dicho ángulo marca la transición entre la aceleración y la relajación.

Análisis cualitativo de la curva de fuerza-tiempo

    Además del análisis de la curva Fuerza-Tiempo de una manera cuantitativa, debemos analizar la huella de la grafica, dicha huella se analizara de una manera cualitativa, basándose en el análisis consecutivo e individualizado de las siguientes variables.

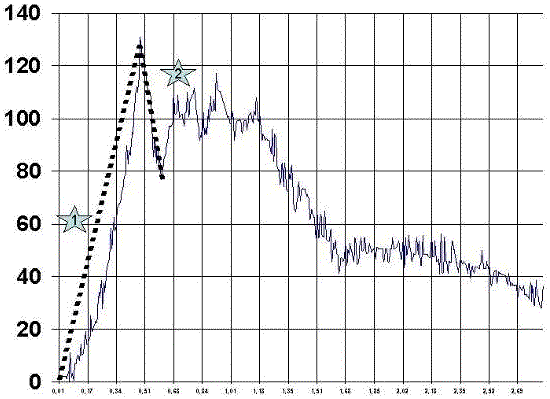
    Definimos 2 secciones a la hora de definir cualitativamente.

    En la fase de aceleración denominada Zona número 1 por tanto, que corresponderá a la hipotenusa del análisis numérico. Estará situada ente los puntos 1 y 2 del gráfico numérico. En dicho zona gráfica se debe valorar tanto la pendiente, que luego se valorara numéricamente con el ángulo alfa 1, como la cualidad de dicho trazado, así como si tiene varios ángulos intermedios en la pendiente. Dicha zona se denomina: Zona de aceleración

    En la fase de relajación o deceleración denominada zona numero 2 del grafico, correspondería a la zona de relajación y se deberá valora tanto la pendiente como la profundidad de la misma. Dicho valor se denomina: Zona de relajación.

Valoración cualitativa de la curva velocidad del disco-tiempo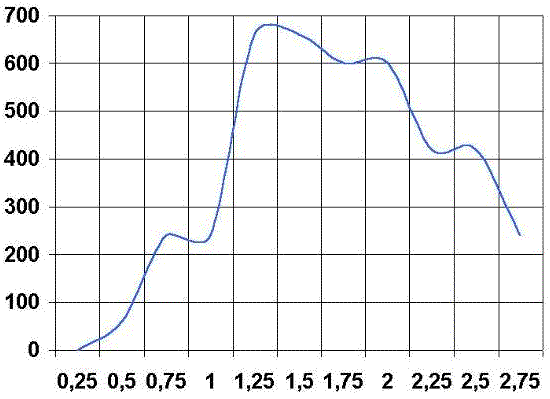

    Para la valoración de la eficiencia del gesto técnico nos vamos a basar en la curva Velocidad del disco-Tiempo (rpm/s). Dicha velocidad refleja la velocidad que el gesto técnico le imprime al volante. Los valores son registrados cada 0.25 segundos y la curva que vamos a analizar surge de la representación de estos valores con respecto al tiempo.

    Para el análisis de la curva velocidad del disco-tiempo vamos a definir de nuevo cuatro puntos:

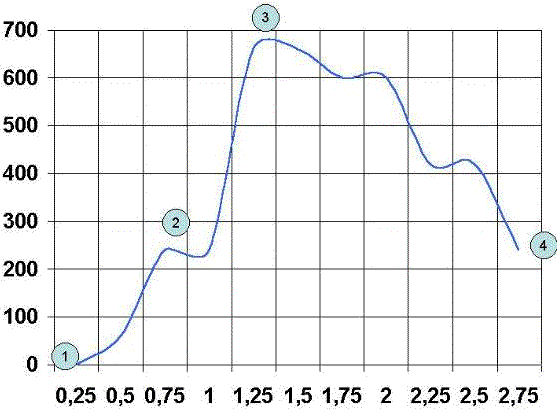
Punto 1: Es el origen de la medición de velocidad. Se mide en revoluciones por minuto. Se denomina Punto de aceleración Inicial.

Punto 2: En muchos casos encontramos un segundo punto de aceleración o de inflexión de la curva. Se mide en revoluciones por minuto. Se denomina, punto de aceleración secundario. Si el impulso es lo suficientemente potente, dicho punto puede desaparecer.

Punto 3: Se alcanza el valor máximo de velocidad. Se mide en revoluciones por minuto, Se denomina Punto de Máxima Velocidad.

Punto 4: Es el final de la curva. Se mide en revoluciones por minuto. Se denomina Punto de deceleración.

    Del análisis de estos 4 puntos obtenemos 6 variables cuantitativas:

Z1 vel: Valor de la velocidad en revoluciones por minuto en el punto 2 o punto de aceleración secundario. Se denomina velocidad de arrancada. Dicho punto puede no aparecer si la zona de arrancada es asumida dentro de la zona de aceleración.

Z1 Ti: Valor en segundos de la zona de arrancada. Es decir tiempo que trascurre entre el punto 1 (punto de aceleración inicial) y el punto 2 (punto de aceleración secundario). Se denomina tiempo de arrancada. Dicho tiempo puede no aparecer si la zona de arrancada es asumida dentro de la zona de aceleración.

Z2 vel: Valor de la velocidad en revoluciones por minuto en el punto 3 o punto de Máxima Velocidad. Se denomina velocidad máxima.

Z2 Ti: Valor en segundos de la zona de aceleración. Es decir en tiempo que trascurre entre el punto 1 (punto de aceleración inicial) y el punto 3 (Punto de Máxima Velocidad). Se denomina tiempo de velocidad máxima

Z3 Vel: Valor de la velocidad en el revoluciones por minuto en el punto 4 o punto de deceleración. Se denomina velocidad final.

Z3 Ti: Valor en segundos de la zona de deceleración. Es decir el tiempo que trascurre entre el punto 3 (punto de Máxima Velocidad) y el punto 4 (Punto de deceleración). Se denomina Tiempo de deceleración.

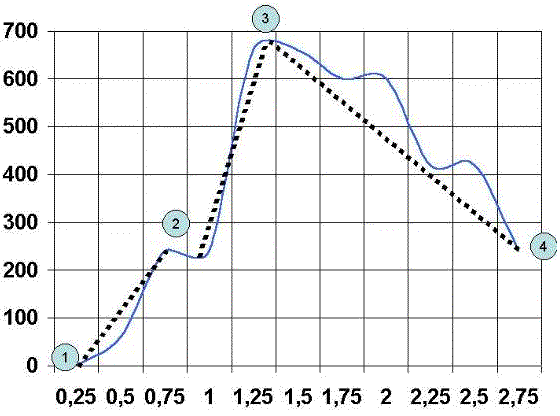
    Si analizamos cualitativamente las curvas velocidad-tiempo. Definimos tres zonas:

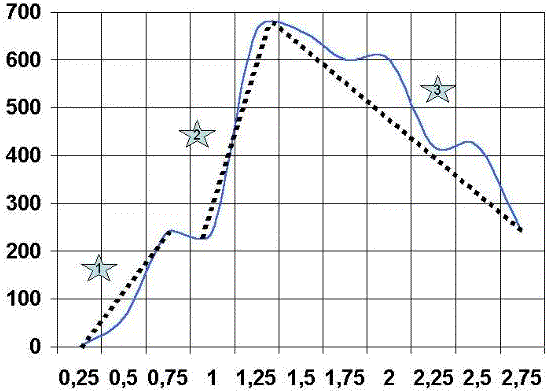
    La primera zona es la zona de aceleración inicial, y es la que va desde el punto 1 al punto 2, pudiendo variar tanto en pendiente como en longitud. Dicho valor se denomina: Zona de arrancada.

    La segunda zona va desde el punto 2 al punto 3, y varía al igual que el anterior en pendiente y en longitud. Dicho valor se denomina: Zona de aceleración.

    La tercera zona va desde el punto 3 al punto 4 y varia igual que el anterior en pendiente y longitud. Dicho valor se denomina: Zona de deceleración.

4. Descripción del movimiento de lanzamiento en suspensión clásico a la altura intermedia del brazo ejecutor

Descripción del test

1º Fase de preparación

    El lanzador debe colocarse con los pies ligeramente separados y colocados simétricamente y con ambas manos a la altura de la cadera.

2º Fase de ejecución

    Se inicia el ciclo impulsando el cuerpo con la pierna contraria al brazo ejecutor, a la vez que la otra pierna se eleva flexionada hacia delante. Durante la ejecución del salto se realiza el armado de brazo, con una sola mano. El brazo ejecutor debe colocarse en posición horizontal y semiflexionado, de manera que el antebrazo está orientado verticalmente, formando entre ambos segmentos corporales un ángulo recto. La cara palmar está dirigida hacia la dirección del lanzamiento y los dedos están orientados hacia arriba. El tronco se torsiona ampliamente hacia el lado del brazo ejecutor. El lanzamiento se realiza en el punto de máxima altura del salto, iniciándose el movimiento de distorsión del tronco súbitamente, se dirige el brazo ejecutor hacia la dirección del lanzamiento y finalizando el movimiento con el impulso final de la muñeca.

3º Fase de relajación

    La parte final del movimiento se completa con el movimiento del brazo ejecutor de forma que cruza el cuerpo y la caída en tierra con las piernas semiflexionadas.

Estudio de las curvas

    Tras la realización del test, vamos a obtener las dos variables estudiadas, La fuerza recogida en la célula de carga y la inercia, recogida en el volante de inercia. Para analizar estas secuencias de datos, se van a representar en función del tiempo.

    Por tanto tras la realización del test, obtendremos dos curvas:

1. La curva fuerza-tiempo: esta curva va a describir la evolución de la fuerza durante el lanzamiento en salto. Dicha curva se va a iniciar con un ascenso que corresponderá a la fase salto, seguido de un descenso que representara el armado del brazo, posteriormente tendremos un nuevo ascenso correspondiente al lanzamiento y un descenso correspondiente a la fase de relajación. Dicha curva va a ser la representación o huella de la fuerza útil del gesto técnico.

2. La curva velocidad del disco-tiempo. Esta curva representa el impulso aplicado sobre el disco, y probablemente, la eficiencia conseguida con el gesto técnico.

    Dichas curvas si bien están correlacionadas, no siguen una distribución paralela, consiguiéndose a iguales valores de fuerza, distintos valores de eficiencia, y viceversa.

Análisis numérico de la curva fuerza-tiempo

    La primera curva que vamos a analizar será la referida a la curva fuerza- tiempo, dicha curva se obtiene del cálculo informático y previamente automatizado de todos los valores obtenidos por la célula de carga al ser ordenados en función del tiempo.

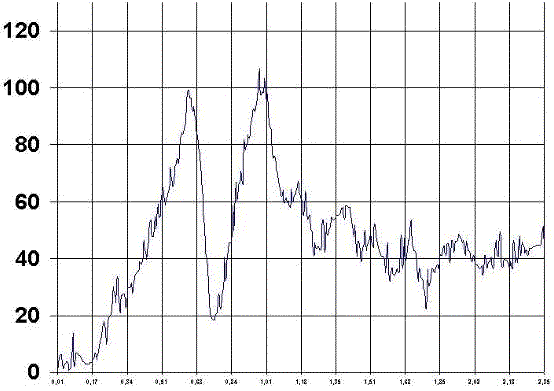
    Para el análisis de esta curva, vamos a definir 10 puntos:

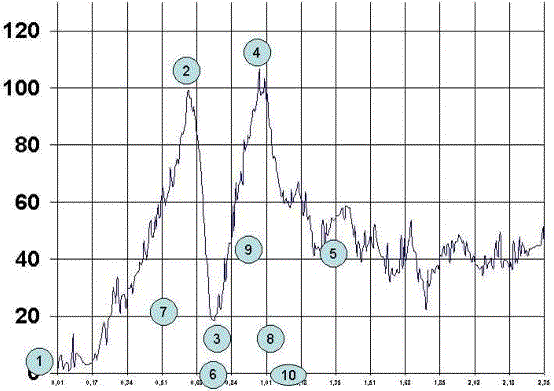
1º punto, donde se inicia la curva. Se mide en centésimas de segundos. Dicho valor se denomina Punto de Arranque del salto.

2º punto, corresponde al pico máximo de la fase de salto. Se mide en Newton. Dicho valor se denomina Punto máximo de salto.

3º punto, corresponde al final de la fase de armado y es el punto correspondiente al valor inferior de esta fase descendente. Se denomina Punto de Arranque del Lanzamiento.

4º punto, corresponde al final de la fase de lanzamiento, corresponde al mayor valor obtenido en la fase de lanzamiento. Se mide en Newton y se denomina. Se denomina Punto máximo del lanzamiento.

5º punto, donde acaba la curva. Se mide en centésimas de segundos. Dicho punto se denomina Punto Final.

6º punto, tiempo de salto, corresponde al valor de tiempo correspondiente con el punto máximo del salto en el lugar de corte perpendicular con el punto 1, se mide en segundos y se denomina Punto referencia en el tiempo de Salto.

7º punto, tiempo de armado, corresponde al valor del tiempo correspondiente con el punto máximo del salto en el lugar de corte perpendicular con el punto 3, se mide en segundos y se denomina punto de referencia inicial del tiempo de armado.

8º punto, tiempo en que se alcanza la fuerza máxima, corresponde al valor del tiempo correspondiente con el punto máximo del lanzamiento en el lugar de corte perpendicular al punto 3. Se mide en centésimas de segundos y se denomina Tiempo de Pico de Fuerza Máxima.

9º punto, corresponde al valor del tiempo correspondiente con el punto máximo del lanzamiento en el lugar de corte perpendicular al punto 5, Se mide en segundos y se denomina punto inicial del tiempo de relajación

10º punto, corresponde al valor de tiempo correspondiente con el punto máximo del lanzamiento en el lugar de corte perpendicular al punto 1. Se mide en segundos y se denomina punto inicial de la fuerza máxima absoluto.

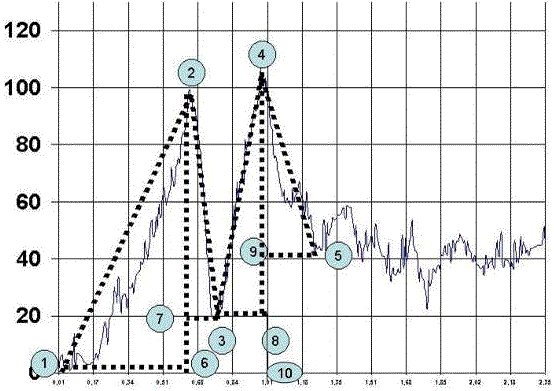
    Del análisis de estos puntos del lanzamiento, podemos definir 4 triángulos.

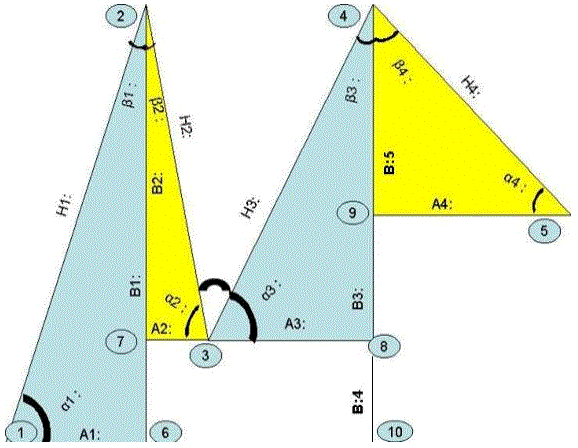
    El primer triangulo situado a la izquierda se denominara triangulo de aceleración del salto. El segundo triangulo situado a la derecha del anterior se denominara triangulo de armado, El tercer triangulo situado a la derecha del anterior, denominara triangulo de aceleración del lanzamiento, mientras que el cuarto triangulo situado a la derecha de denominara triangulo de relajación del lanzamiento.

    En dichos triángulos vamos a definir los siguientes valores:

A1: Si unimos el punto 1 y el punto 6 obtenemos el valor del tiempo que el deportista tarda en alcanzar el máximo, Aunque este valor se dibuje gráficamente en centésimas de segundos a la hora de tratar los datos numéricamente de debe de referir en segundos. Dicho valor se denomina: Tiempo de aceleración del salto.

A2: Si unimos el punto 7 y el punto 3, obtenemos el valor del tiempo que el deportista tarda armar el golpeo. Aunque este valor se dibuje gráficamente en centésimas de segundos, a la hora de tratar los datos numéricamente de debe de referir en segundos. Dicho valor se denomina: Tiempo de armado.

B1: Si unimos el punto 2 y el punto 6, obtenemos el valor de la fuerza máxima alcanzada por el deportista en el salto, dicho valor se mide en Newton y se denomina: Pico de Fuerza Máxima del salto.

B2: Si unimos el punto 2 y el punto 7, obtenemos el valor de la pérdida de fuerza alcanzada por el deportista en la fase de armado, dicho valor se mide en Newton y se denomina: Pérdida de Fuerza durante la fase de armado.

H1: Si unimos el punto 1 y el punto 2, obtenemos el valor de la hipotenusa ascendente, para hacerlos debemos de aplicar el teorema de Pitágoras que dice que H1²= A1²+B1², por tanto H1= A1²+B1². Dicho valor se denomina hipotenusa de Aceleración del salto.

FE: Para valorar la fuerza explosiva tradicionalmente se ha relacionado la fuerza máxima con el tiempo tardado en producirla. Así en nuestra curva la fuerza explosiva seria la relación existente entre B1 y A1 (FES) o entre B3 y A3 (FET), siguiendo la formula⁽³⁾:

Fuerza explosiva (N*s^-1) = Fuerza máxima (N)/ Tiempo de aceleración (s)

Siendo la relación entre B1y A1 la Fuerza explosiva del salto (FES) y entre B3 y A3 la fuerza explosiva del lanzamiento (FEL)

Alfa 1: ángulo que muestra la pendiente del grafico y se calcula mediante la siguiente fórmula Alfa 1=cos^-1 (A1/H1). Se mide en grados. Dicho ángulo se denomina Angulo de aceleración del salto.

Beta 1: Angulo que cierra el triangulo se calcula mediante la formula Beta1= 90-alfa1. Se mide en grados. Dicho ángulo se denomina, Angulo complementario de la aceleración del salto.

H2: Si unimos el punto 2 y el punto 3, obtenemos el valor de la hipotenusa descendente correspondiente al armado del brazo. Para hacerlo debemos aplicar el teorema de Pitágoras, que dice que H2²= A2²+B2², por tanto H2= A2²+B2². Dicho valor se denomina hipotenusa de armado

Alfa 2: ángulo que muestra la pendiente del grafico y se calcula mediante la siguiente fórmula Alfa 2=cos^-1 (A2/H2). Se mide en grados. Dicho ángulo se denomina ángulo complementario del armado.

Beta 2: Angulo que cierra el triangulo. Se calcula mediante la fórmula Beta2= 90-alfa2. Se mide en grados. Dicho ángulo se denomina ángulo de armado

Angulo superior del primer y segundo triángulos: Se obtiene de la suma de los dos ángulo Beta (ángulos complementarios de aceleración y relajación respectivamente). Mediante la formula Angulo superior primer y segundo triángulos = Beta 1 + Beta 2. Se mide en grados. Dicho ángulo marca la transición entre el salto y el armado

A3: Si unimos el punto 3 y el punto 8 obtenemos el valor del tiempo que el deportista tarda en alcanzar la máxima potencia de lanzamiento, Aunque este valor se dibuje gráficamente en centésimas de segundos a la hora de tratar los datos numéricamente de debe de referir en segundos. Dicho valor se denomina: Tiempo de aceleración del lanzamiento.

A4: Si unimos el punto 9 y el punto 5 obtenemos el valor del tiempo que el deportista tarda en relajar el lanzamiento. Aunque este valor se dibuje gráficamente en centésimas de segundos, a la hora de tratar los datos numéricamente de debe de referir en segundos. Dicho valor se denomina: Tiempo de relajación.

B3: Si unimos el punto 4 y el punto 8, obtenemos el valor de la fuerza máxima alcanzada por el deportista en el lanzamiento, dicho valor se mide en Newton y se denomina: Pico Relativo de Fuerza Máxima del lanzamiento. Este punto mide la fuerza máxima lograda por el lanzamiento tras despreciar la fuerza generada en el lanzamiento.

B4: Si unimos El punto 4 y el punto 9 Observamos el valor de la fuerza máxima alcanzada por el deportista al sumar la inercia del salto al lanzamiento. Dicho valor se mide en Newton y se denomina: Pico de Fuerza Máxima Absoluto. Este punto mide la fuerza máxima lograda por el lanzamiento sumado al impulso cinético almacenado en el salto.

B5: Si unimos el punto 4 y el punto 9, obtenemos el valor de la pérdida de fuerza alcanzada por el deportista en la fase relajación del lanzamiento, dicho valor se mide en Newton y se denomina: Pérdida de Fuerza durante la fase de relajación.

H3: Si unimos el punto 3 y el punto 4, obtenemos el valor de la hipotenusa ascendente, para el tercer triangulo para hacerlos debemos de aplicar el teorema de Pitágoras que dice que H3²= A3²+B3², por tanto H3= A3²+B3². Dicho valor se denomina hipotenusa de Aceleración del lanzamiento.

Alfa 3: ángulo que muestra la pendiente del grafico y se calcula mediante la siguiente fórmula Alfa 3=cos^-1 (A3/H3). Se mide en grados. Dicho ángulo se denomina Angulo de aceleración del lanzamiento.

Beta 3: Angulo que cierra el triangulo se calcula mediante la formula Beta3= 90-alfa3. Se mide en grados. Dicho ángulo se denomina, Angulo complementario de la aceleración del lanzamiento.

H4: Si unimos el punto 4 y el punto 5, obtenemos el valor de la hipotenusa descendente correspondiente al armado del brazo. Para hacerlo debemos aplicar el teorema de Pitágoras, que dice que H4²= A4²+B4², por tanto H4= A4²+B4². Dicho valor se denomina hipotenusa de relajación

Alfa 4: ángulo que muestra la pendiente del grafico y se calcula mediante la siguiente fórmula Alfa 4=cos^-1 (A4/H4). Se mide en grados. Dicho ángulo se denomina ángulo complementario de relajación.

Beta 4: Angulo que cierra el triangulo. Se calcula mediante la fórmula Beta4= 90-alfa4. Se mide en grados. Dicho ángulo se denomina ángulo de relajación

Angulo superior del tercer y cuarto triangulo: Se obtiene de la suma de los dos ángulo Beta (ángulos complementarios de aceleración y relajación respectivamente). Mediante la formula Angulo superior del tercer y cuarto triangulo Beta 3 + Beta 4. Se mide en grados. Dicho ángulo marca la transición entre la aceleración y la relajación.

Angulo inferior: Se obtiene de la suma de los ángulos Alfa 2 (ángulo complementario del armado) y el Alfa 3 (ángulo de aceleración del lanzamiento). Mediante la formula Angulo inferior = 180- (Alfa 2 + Alfa 3). Se mide en grados. Dicho ángulo marca la transición entre el armado y el lanzamiento.

Análisis cualitativo de la curva de fuerza-tiempo

    Además del análisis de la curva Fuerza-Tiempo de una manera cuantitativa, debemos analizar la huella de la grafica, dicha huella se analizara de una manera cualitativa, basándose en el análisis consecutivo e individualizado de las siguientes variables.

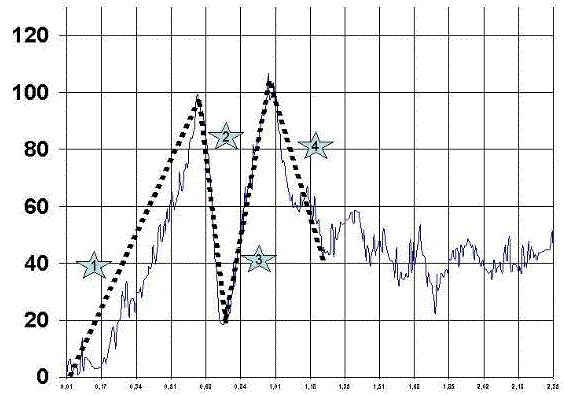
    Definimos 4 secciones a la hora de definir cualitativamente.

    En la fase de salto denominada Zona número 1 por tanto, que corresponderá a la hipotenusa del salto del análisis numérico. Estará situada ente los puntos 1 y 2 del gráfico numérico. En dicho zona gráfica se debe valorar tanto la pendiente, que luego se valorara numéricamente con el ángulo alfa 1, como la cualidad de dicho trazado, así como si tiene varios ángulos intermedios en la pendiente. Dicha zona se denomina: Zona de salto

    En la fase de armado denominada zona numero 2 del grafico, correspondería a la zona de armado y se deberá valora tanto la pendiente como la profundidad de la misma. Dicho valor se denomina: Zona de armado.

    En la fase de lanzamiento denominada Zona número 3 por tanto, que corresponderá a la hipotenusa del lanzamiento del análisis numérico. Estará situada ente los puntos 3 y 4 del gráfico numérico. En dicho zona gráfica se debe valorar tanto la pendiente, que luego se valorara numéricamente con el ángulo alfa 2, como la cualidad de dicho trazado, así como si tiene varios ángulos intermedios en la pendiente. Dicha zona se denomina: Zona de lanzamiento

    En la fase de relajación denominada zona numero 3 del grafico, correspondería a la zona de relajación y se deberá valora tanto la pendiente como la profundidad de la misma. Dicho valor se denomina: Zona de relajación.

Valoración cualitativa de la curva velocidad del disco-tiempo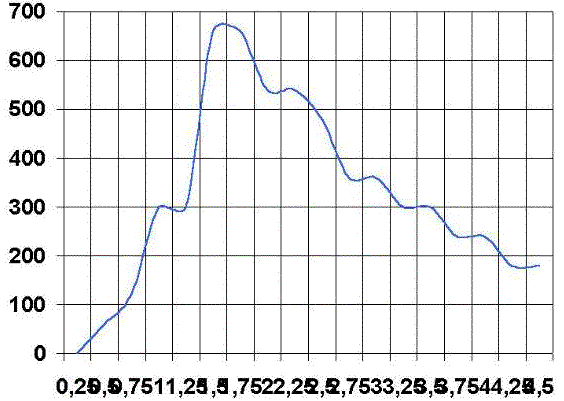

    Para la valoración de la eficiencia del gesto técnico nos vamos a basar en la curva Velocidad del disco-Tiempo (rpm/s). Dicha velocidad refleja la velocidad que el gesto técnico le imprime al volante. Los valores son registrados cada 0.25 segundos y la curva que vamos a analizar surge de la representación de estos valores con respecto al tiempo.

    Para el análisis de la curva velocidad del disco-tiempo vamos a definir de nuevo cuatro puntos:

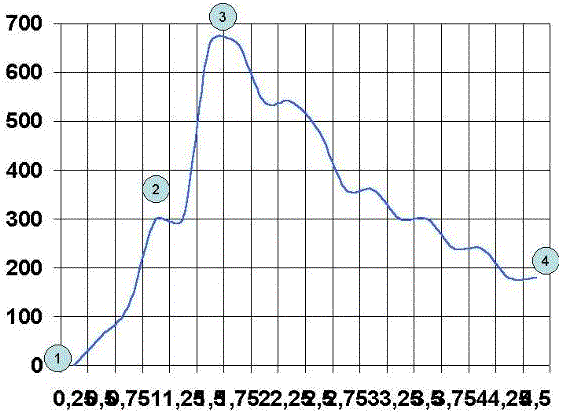
Punto 1: Es el origen de la medición de velocidad. Se mide en revoluciones por minuto. Se denomina Punto de aceleración Inicial.

Punto 2: En muchos casos encontramos un segundo punto de aceleración o de inflexión de la curva. Se mide en revoluciones por minuto. Se denomina, punto de aceleración secundario. Si el impulso es lo suficientemente potente, dicho punto puede desaparecer.

Punto 3: Se alcanza el valor máximo de velocidad. Se mide en revoluciones por minuto, Se denomina Punto de Máxima Velocidad.

Punto 4: Es el final de la curva. Se mide en revoluciones por minuto. Se denomina Punto de deceleración.

    Del análisis de estos 4 puntos obtenemos 6 variables cuantitativas:

Z1 vel: Valor de la velocidad en revoluciones por minuto en el punto 2 o punto de aceleración secundario. Se denomina velocidad de arrancada. Dicho punto puede no aparecer si la zona de arrancada es asumida dentro de la zona de aceleración.

Z1 Ti: Valor en segundos de la zona de arrancada. Es decir tiempo que trascurre entre el punto 1 (punto de aceleración inicial) y el punto 2 (punto de aceleración secundario). Se denomina tiempo de arrancada. Dicho tiempo puede no aparecer si la zona de arrancada es asumida dentro de la zona de aceleración.

Z2 vel: Valor de la velocidad en revoluciones por minuto en el punto 3 o punto de Máxima Velocidad. Se denomina velocidad máxima.

Z2 Ti: Valor en segundos de la zona de aceleración. Es decir en tiempo que trascurre entre el punto 1 (punto de aceleración inicial) y el punto 3 ( Punto de Máxima Velocidad). Se denomina tiempo de velocidad máxima

Z3 Vel: Valor de la velocidad en el revoluciones por minuto en el punto 4 o punto de deceleración. Se denomina velocidad final.

Z3 Ti: Valor en segundos de la zona de deceleración. Es decir el tiempo que trascurre entre el punto 3 (punto de Máxima Velocidad) y el punto 4 ( Punto de deceleración). Se denomina Tiempo de deceleración.

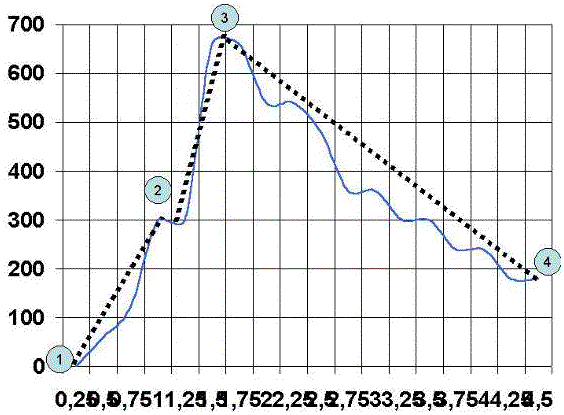
    Si analizamos cualitativamente las curvas velocidad-tiempo. Definimos tres zonas:

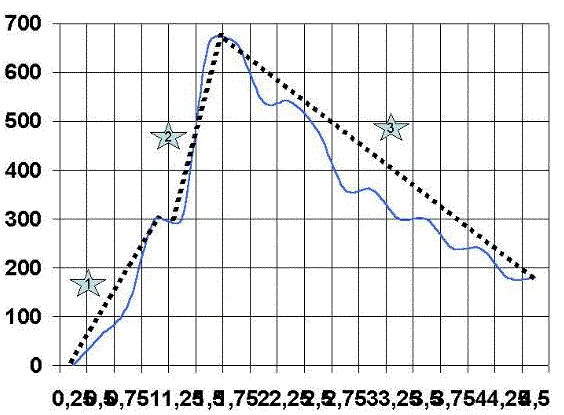
    La primera zona es la zona de aceleración inicial, y es la que va desde el punto 1 al punto 2, pudiendo variar tanto en pendiente como en longitud. Dicho valor se denomina: Zona de arrancada.

    La segunda zona va desde el punto 2 al punto 3, y varía al igual que el anterior en pendiente y en longitud. Dicho valor se denomina: Zona de aceleración.

    La tercera zona va desde el punto 3 al punto 4 y varia igual que el anterior en pendiente y longitud. Dicho valor se denomina: Zona de deceleración.

Comparación curvas fuerza-tiempo de los distintos golpeos de balonmano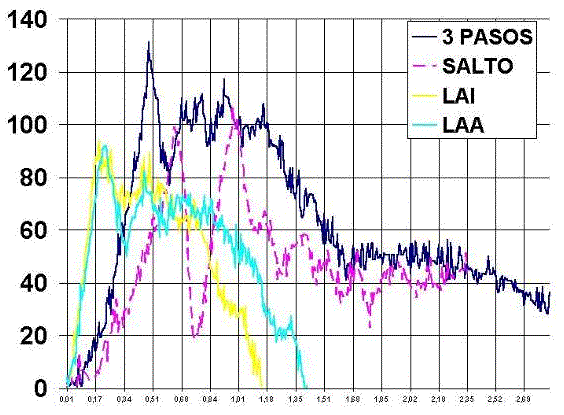

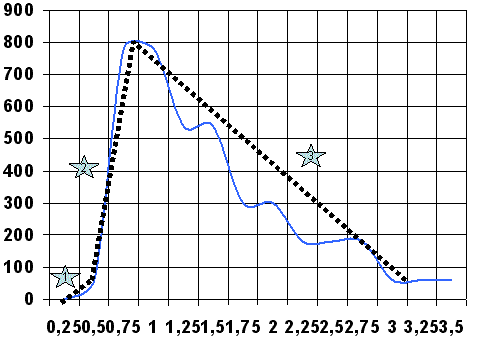
    Al realizar el grafico comparativo de los 4 golpeos observamos como el golpeo alto y de altura intermedia tiene una zona de aceleración parecida diferenciándose claramente en la zona de relajación, ya que el lanzamiento de altura intermedia tiene una menor perdida de fuerza en dicha relajación, además el final de golpeo se produce antes en este lanzamiento que en lanzamiento alto. Si nos fijamos en el lanzamiento en salto y el lanzamiento en 3 pasos estos tiene un mayor tiempo de aceleración con una mayor duración. El gesto que más fuerza útil consigue es el lanzamiento de tres pasos seguido del lanzamiento en salto, dicha diferencia se explica por la inercia acumulada previa al lanzamiento, llama la atención que el lanzamiento alto y el lanzamiento de altura intermedia obtienen fuerzas similares en tiempos de aceleración similares.

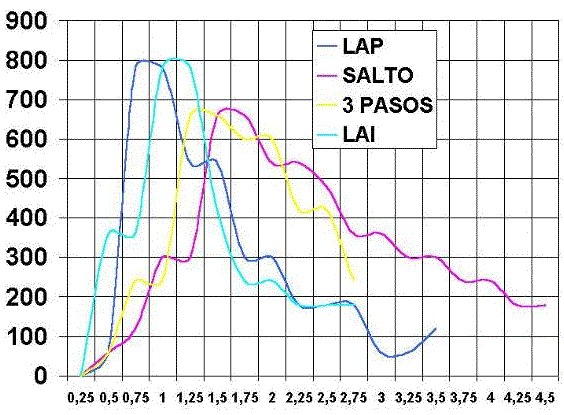
    Si analizamos la curva inercia del disco tiempo observamos también dos claros patrones en los que la mayor inercia del disco (al ser movimientos más puros) se consigue en el lanzamiento alto e intermedio consiguiendo ambos 800 rpm pero la velocidad máxima del lanzamiento intermedio es superior al del lanzamiento superior. Los lanzamientos en salto, logran menor velocidad máxima y en un mayor tiempo.

Discusión

    Para la valoración de la fuerza en balonmano se han utilizado diferentes test como la 1 RM^(4,5,6,7) el test de Bosco^{(4,8,5,9,10,11,12,13)}, test de Wingate⁽¹⁰⁾, lanzamiento de balón medicinal⁽⁹⁾, valoraciones neuromusculares⁽⁴⁾, dinamómetros isocinéticos^(4,11,12,14), estudios cinemáticos^{(4,6,14,15,16)}, determinaciones hormonales⁽¹²⁾, electromiografía⁽¹⁵⁾, goniómetros digitales⁽⁸⁾ o incluso métodos indirectos de medida de la fuerza como la masa muscular calculada mediante antropometría^(4,9,17,18). Pero ninguno de estos métodos valora la fuerza útil del lanzamiento, por tanto no existen claras concordancias entre los valores de fuerza medidos por las medidas tradicionales y el rendimiento deportivo.

    La fuerza se puede definir según Letzelter⁽¹⁷⁾ como la mayor fuerza que es capaz de desarrollar el sistema nervioso y muscular por medio de una contracción máxima voluntaria. Para Bührle⁽¹⁸⁾ la fuerza máxima es la parte de la fuerza absoluta que puede ser activada de forma voluntaria. Para Bosco⁽¹⁹⁾ la fuerza máxima es la capacidad de desarrollar fuerza que permite movilizar una carga máxima que no permite modular la velocidad de ejecución. González y Gorostiaga⁽²⁰⁾ señalan que "la fuerza isométrica máxima se produce cuando el sujeto realiza una contracción voluntaria máxima contra una resistencia insalvable".

    La fuerza en balonmano⁽²¹⁾ en lugar de las tradicionales fuerza-resistencia, fuerza-máxima y fuerza-explosiva, las categorías de fuerza en balonmano deben ser fuerza de lanzamiento, fuerza de lucha, fuerza de salto y fuerza de desplazamiento, ya que ese trabajo va destinado a los grupos musculares responsables de producir la fuerza necesaria para esas acciones. Por tanto el trabajo de fuerza se debe de basar en la ganancia de fuerza útil en estos subtipos de fuerza.

    Tras estudios como los de Gorostiaga⁽⁴⁾ sabemos que trabajos de 6 semanas de fuerza máxima logran un aumento de la fuerza máxima y la velocidad, pero debemos realizar estudios que nos demuestren ganancias en la fuerza útil de los diferentes lanzamientos, ya que la fuerza útil (y no la fuerza máxima) es que se relaciona con el rendimiento deportivo⁽³⁾.

    En los deportes colectivos, de todas las manifestaciones de fuerza, la fuerza explosiva o capacidad para generar fuerza en el menor tiempo posible es la más importante. La fuerza máxima es uno de los factores de los que depende la fuerza explosiva ^(20,22,23); aquella es "requerida en pocas condiciones específicas durante la competición" ⁽²⁴⁾, pero una buena formación de esta capacidad, permite la obtención de resultados óptimos en la mayoría de acciones deportivas donde haya que mover masas externas o el propio cuerpo a gran velocidad ⁽²⁵⁾; algunos estudios muestran correlaciones significativas entre la velocidad con la que se alcanza un alto grado de tensión intramuscular en una contracción isométrica y el rendimiento en el gesto deportivo ⁽²⁶⁾.

    Tradicionalmente el trabajo de fuerza en balonmano se ha realizado trabajando en dos periodos un periodo preparatorio y un periodo competitivo. En el periodo preparatorio la fuerza se ha trabajado usando primero una fase de fuerza resistencia, seguidos de una fase de trabajo de fuerza máxima, traspasando esta a fuerza explosiva. Pasando de ejercicios generales a ejercicios dirigidos. En el periodo competitivo el trabajo de fuerza se ha realizado con sesiones de fuerza explosiva con ejercicios dirigidos, intercalados con sesiones de fuerza máxima. Pero este tipo de trabajo de fuerza debería ser monitorizado con los test que hemos diseñado para valorar la eficiencia y efectividad de estos programas, depurándolos y personalizándolos hasta lograr un trabajo personalizado y eficiente de la fuerza en jugadores de balonmano.

    Gorostiaga⁽⁵⁾ demuestra en un reciente estudio que un programa de entrenamiento puede afectar de manera diferente al tren superior y al tren inferior. Este estudio indicaría que valoraciones del tren inferior como el test de Bosco o el test de Wingate no servirían para la monitorización de la fuerza del tren superior en jugadores de balonmano, por lo que deberíamos de usar test específicos para la valoración de la fuerza en jugadores de balonmano, justificando la necesidad de crear test que valoren la fuerza útil de nuestro jugadores.

    Test similares a los cuatro test del Atlas para balonmano se han realizado para bádminton ^(1,27), fútbol ^(2,28), tenis (pendiente de publicación) y voleibol (pendiente de publicación). Dichos test abren un nuevo campo en la valoración de la fuerza útil, la valoración y monitorización del entrenamiento y la mejora del rendimiento deportivo.

    Gorostiaga demuestra que la fuerza muscular y la masa muscular ⁽¹⁷⁾ significan una ventaja para los jugadores de balonmano. Además este artículo relaciona la eficiencia en la velocidad de lanzamiento en jugadores de elite con la fuerza del tren superior, demostrando la importancia que el trabajo muscular tiene en el rendimiento deportivo.

    Tradicionalmente se han asociado diferentes valores de fuerza en función del sexo, pero de los análisis de van den Tillar⁽¹⁴⁾ se deduce que no hay diferencias en función del genero y que las diferencias observados pueden ser debidas a la diferente masa muscular.

    Bayios⁽¹¹⁾ estudia la relación entre la fuerza del hombro y la velocidad de lanzamiento. No encuentra relación entre la fuerza (calculada utilizando un dinamómetro isocinético) y la velocidad de lanzamiento. Este sorprendente resultado se podría explicar debido a que los dinamómetros isocinéticos miden la fuerza de una cadena cinética cerrada, mientras que el lanzamiento supone una cadena muscular más amplia que la analizada por este dinamómetro, en posteriores estudios deberemos analizar la correlación^(29,30,31) y concordancia^(29,30,31) entre nuestra maquina y la velocidad de lanzamiento.

    Igual que otras características de los jugadores de balonmano como el somatotipo ⁽³²⁾ varían en función del puesto, creemos que los valores de fuerza útil también cambiaran en función del puesto analizado, por lo que se deberían realizar estudios de la fuerza útil en función del puesto analizado.

Bibliografía

1. Garrido Chamorro R.P. Blasco Lafarga C. Albert Jiménez A. Perez Turpin J.A. Navlaon J. Un nuevo test para medir la fuerza útil en badminton. Lecturas: Educación física y deportes nº 93 Febrero del 2005.

2. Blasco Lafarga, C. Garrido Chamorro, R.P. Albert Jiménez, A. Un nuevo test para medir la fuerza útil en el fútbol. Efdeportes.com Nº 96

3. González Badillo, J.J., Ribas, J. Bases de la programación del entrenamiento de fuerza. Inde, Barcelona, 2002

4. Gorostiaga E. Izquierdo M, Iturralde P, Ruesta M., Ibáñez J. Effects of heavy resistant on maximal and explosive force production, endurance and serum hormones in adolescent handball player. Eur J Appl Physiol (1999),80;485-493

5. Gorostiaga EM, Granados C, Ibanez J, Gonzalez-Badillo JJ, Izquierdo M. Effects of an entire season on physical fitness changes in elite male handball players. Med Sci Sports Exerc. 2006 Feb; 38(2):357-66.

6. Gorostiaga EM, Granados C, Ibanez J, Izquierdo M. Differences in physical fitness and throwing velocity among elite and amateur male handball players. Int J Sports Med. 2005 Apr; 26(3):225-32.

7. Izquierdo M, Hakkinen K, Gonzalez-Badillo JJ, Ibanez J, Gorostiaga EM. Effects of long-term training specificity on maximal strength and power of the upper and lower extremities in athletes from different sports. Eur J Appl Physiol. 2002 Jul; 87(3):264-71. Epub 2002 May 22.

8. Vicente-Rodriguez G.; Dorado C.; Perez-Gomez J.; Gonzalez-Henriquez J.J.; Calbet J.A.L; Enhanced bone mass and physical fitness in young female handball players. Bone 35 (2004) 1208-1215.

9. Ruiz Martínez E. La planificación anual del entrenamiento de preparación física. Las cualidades motrices y la condición física aplicada al balonmano. 1985

10. Bencke J, Damsgaard R, Saekmose A, Jorgensen P, Jorgensen K, Klausen K. Anaerobic power and muscle strength characteristics of 11 years old elite and non-elite boys and girls from gymnastics, team handball, tennis and swimming. Scand J Med Sci Sports. 2002 Jun; 12(3):171-8.

11. Bayios IA, Anastasopoulou EM, Sioudris DS, Boudolos KD. Relationship between isokinetic strength of the internal and external shoulder rotators and ball velocity in team handball. J Sports Med Phys Fitness. 2001 Jun; 41(2):229-35.

12. Gorostiaga EM, Izquierdo M, Iturralde P, Ruesta M, Ibanez J. Effects of heavy resistance training on maximal and explosive force production, endurance and serum hormones in adolescent handball players. Eur J Appl Physiol Occup Physiol. 1999 Oct;80(5):485-93.

13. Salvador Olaso Climent, A. Martín Ezpeleta, Jordi Martínez Pardo, Antoni Planas Anzano. Variación de la potencia del tren inferior en jugadoras de balonmano de alta competición. Apuntes: Educación física y deportes, Nº 76, 2004, pags. 35-42.

14. Van den Tillaar R, Ettema G. Effect of body size and gender in overarm throwing performance. Eur J Appl Physiol. 2004 Apr;91(4):413-8. Epub 2003 Nov 18.

15. Simonsen E.B.; Magnusson S.P.; Bencke J. Naesborg H; Havkrog M. Ebstrup J.F; Sorensen H. Can the hamstring muscles Project the anterior cruciate ligament durin a side-cutting maneuver? . Scand J Med Sci Sports 2000: 10:78-84.

16. Jöris H.J.J; Edwards van Muyen A.J; van Ingen Schenau G.J; Kemper H.C.G. Force, velocity and energy flow during the overarm throw in female handball players. Journal of Biomechanics Vol 18;6, 1985 409-414.

17. Letzeletr, H.; Letzeletr, M. (1990). Entraînement de la force. Vigot. Paris.

18. Bührle, M. (1990). El concepto básico del entrenamiento de fuerza y fuerza de salto.

19. Bosco, C. (1994). La valoración de la fuerza con el test de Bosco. Paidotribo. Barcelona.

20. González-Badillo, J.J.; Gorostiaga. (1995). Fundamentos del entrenamiento de la fuerza. INDE. Barcelona.

21. Espar, X. (1995). La preparación física específica en los deportes colectivos. Orientaciones metodológicas. Curso de Verano del INEF de Castilla y León -1995-. Junta de Castilla y León, León.

22. Vélez, M. (1992). El entrenamiento de fuerza para la mejora del salto. Apuntes, 29 (112): 139-156.

23. Vidal, M. (2000). La fuerza en el Deporte. Sistemas de entrenamiento con cargas. Esteban Sanz. Madrid.

24. Hauptmann, M.; Harre, D .(1987). El entrenamiento de la fuerza máxima. RED, 1 (2): 11-18.

25. Chirosa, L.J. (1998). Eficacia del entrenamiento con un método de contraste para la mejora de la fuerza de impulsión en relación a otro de tipo convencional en balonmano. Tesis doctoral. Universidad de Granada.

26. Vitalaso, J.T.; Aura, O. (1984). Seasonal fluctuations of force production in high jumpers. Canadian Journal Applied Sport Sciences, 9 (4): 209-013.

27. Blasco Lafarga C, Garrido Chamorro R.P, Albert Jiménez A. Test Atlas para Bádminton. Archivos de medicina del deporte volumen XXII Nº 110- 2005 Pág. 525.

28. Albert Jiménez A, Garrido Chamorro R.P, Blasco Lafarga C. Test Atlas para Fútbol. Archivos de medicina del deporte volumen XXII Nº 110- 2005 Pág. 525-526

29. Ludbrook J. Statistics in physiology and pharmacology: a slow and erratic learning curve. Clin Exp Pharmacol Physiol. 2001 May-Jun;28(5-6):488-92. Review.

30. Atkinson G, Nevill AM. Statistical methods for assessing measurement error (reliability) in variables relevant to sports medicine. Sports Med. 1998 Oct;26(4):217-38. Review.

31. Ludbrook J. Comparing methods of measurements. Clin Exp Pharmacol Physiol. 1997 Feb;24(2):193-203. Review.

32. L. Ruiz, José Enrique Egocheaga Rodríguez. Estudio del somatotipo en jugadoras de balonmano por puestos y categorías / Apuntes: Medicina de l'esport, Vol. 36, Nº 137, 2001, págs. 25-32.

	Web EFDeportes.com
revista digital · Año 11 · N° 102 | Buenos Aires, Noviembre 2006   © 1997-2006 Derechos reservados